Một ít về B-Tree
Bài đăng này đã không được cập nhật trong 4 năm
Bài viết được dịch từ nguồn: https://dev.mysql.com/doc/refman/5.7/en/mysql-indexes.html http://www.geeksforgeeks.org/b-tree-set-1-introduction-2/
Như ta đã biết Index giúp cho MySql tìm kiếm các bản ghi nhanh chóng, có thể hiểu nôm na Index như phần mục lục trong 1 quyển sách, nhờ đó ta có thể tìm kiếm nội dung cần thiết thông qua phần mục lục thay vì lật rở cả cuốn sách.
Index được MySql lưu giữ tại B-Trees, trong vài trường hợp ngoại lệ, có thể được lưu tại R-Trees. Vậy B-Trees là gì và được cấu trúc như thế nào.
Introduction
B-Tree là cây tìm kiếm tự cân bằng. Trong hầu hết các cây tìm kiếm tự cân bằng khác (như AVL và Red Black Trees), giả định rằng mọi thứ đều nằm trong bộ nhớ chính. Để hiểu được việc sử dụng B-Trees, chúng ta phải nghĩ đến số lượng dữ liệu khổng lồ mà không thể lưu trong bộ nhớ chính. Khi số lượng keys lớn, dữ liệu được đọc từ hard disk dưới dạng khối (blocks). Thời gian đọc dữ liệu từ hard disk rất lâu so với thời gian truy xuất bộ nhớ chính, Ý tưởng chính của việc sử dụng B-Trees là giảm số lần truy cập đĩa. Hầu hết các hoạt động của cây (tìm kiếm, chèn, xóa, max, min, ..etc) yêu cầu truy cập đĩa O (h) chính là chiều cao của B-Trees. B-Trees là fat trees. Chiều cao của cây B được hạn chế tối đa bằng việc bố trí nhiều nhất keys tại các node. Nói chung kích thước node tương đương kích thước block. Vì khả năng hạn chế h, tổng số lần đĩa truy cập cho hầu hết các hoạt động được giảm đáng kể so với Cây tìm kiếm cân bằng nhị phân như cây AVL, Red Black Tree, ..etc.
Thuộc tính của B-Tree
- Tất cả lá ở cùng cấp.
- Một B-Tree được xác định bằng thuật ngữ tối thiểu 't'. Giá trị của t phụ thuộc vào kích thước khối đĩa.
- Mỗi node trừ root phải chứa ít nhất t-1 keys. Gốc có thể chứa tối thiểu 1 node.
- Tất cả các node (bao gồm cả gốc) có thể chứa nhiều nhất 2t - 1 keys.
- Số con của một node bằng số keys trong đó cộng với 1.
- Tất cả các keys của một node được sắp xếp theo thứ tự ngày càng tăng. Child giữa hai keys k1 và k2 chứa tất cả các keys nằm trong khoảng từ k1 và k2.
- B-Tree phát triển và co lại từ gốc mà không giống như cây tìm kiếm nhị phân. Cây tìm kiếm nhị phân phát triển rộng dần.
- Giống như cây tìm kiếm nhị phân cân bằng, sự phức tạp về thời gian để tìm kiếm, chèn và xóa là khá lớn.
Sau đây là một ví dụ B-Tree mức độ tối thiểu 3. Lưu ý rằng trong thực tế B-Cây, giá trị của mức độ tối thiểu là nhiều hơn 3.
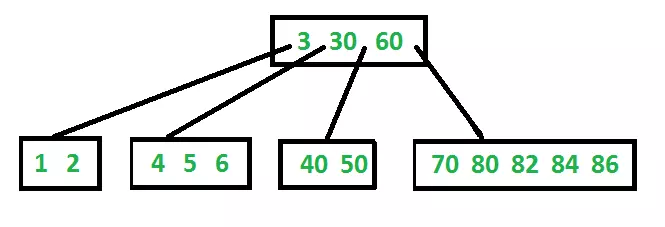
Tìm kiếm
Tìm kiếm tương tự như tìm kiếm trong Cây tìm kiếm nhị phân. Hãy tìm chìa khóa để tìm k. Chúng ta bắt đầu từ gốc và đệ quy đi qua. Đối với mỗi node không có nhánh sẽ không xét đến, nếu node có key, chúng ta chỉ cần trả lại node. Nếu không, chúng ta sẽ quay trở lại child thích hợp (The child ngay trước key) của node. Nếu chúng ta đạt đến một node và không tìm thấy k trong node leaf, chúng ta sẽ trả về NULL.
Traverse
Traversal cũng tương tự như Invers traversal của cây nhị phân. Chúng tôi bắt đầu từ child ở bên trái, in lại các child còn lại bên trái, sau đó lặp lại quá trình tương tự cho child và key còn lại. Cuối cùng, in ngược lại child đầu bên phải.
Insert
Một key mới luôn được chèn vào tại node leaf. Gọi key được chèn vào là k. Giống như BST, chúng ta bắt đầu từ gốc và đi xuống cho đến khi chúng ta tìm được một node leaf. Khi chúng ta tìm được một node leaf, chúng ta chèn keys vào node leaf đó. Không giống như BST, chúng ta có một phạm vi được xác định trước về số lượng các keys mà một node có thể chứa. Vì vậy, trước khi chèn một key vào node, chúng tôi đảm bảo rằng node có thể được add thêm key.
Làm thế nào để đảm bảo rằng một node có không gian có sẵn cho key trước khi key được chèn vào? Chúng tôi sử dụng một method được gọi là splitChild () được sử dụng để phân chia một child của một node. Xem biểu đồ dưới đây để hiểu được sự phân chia. Trong sơ đồ sau, child y của x đang được chia thành hai node y và z. Lưu ý rằng các method splitChild di chuyển một key lên và đây là lý do B-Trees lớn lên không giống như BSTs phát triển.
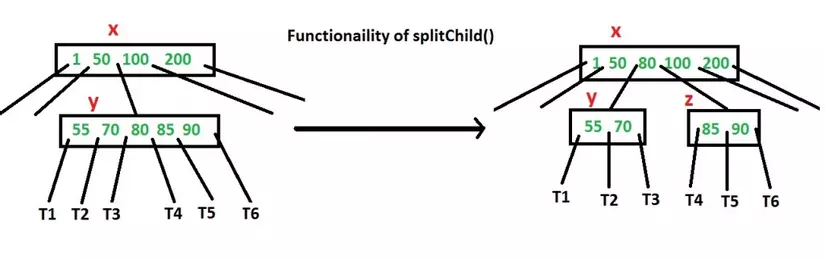
Như đã thảo luận ở trên, để chèn một key mới, chúng ta đi từ gốc tới leaf. Trước khi đi qua một node, đầu tiên chúng ta kiểm tra xem node đã đầy. Nếu node là đầy, chúng tôi chia nó để tạo không gian.
Deletion process
Xoá từ B-Trees là phức tạp hơn là chèn, bởi vì chúng ta có thể xóa một khoá từ bất kỳ node nào - không chỉ là leaf - và khi chúng ta xóa một key một node, chúng ta sẽ phải sắp xếp lại các child của node.
Như trong chèn, chúng ta phải đảm bảo xóa không vi phạm các thuộc tính của cây B. Cũng như chúng ta phải đảm bảo rằng một node không bị quá lớn do chèn, chúng ta phải đảm bảo rằng một node không quá nhỏ trong quá trình xóa (ngoại trừ gốc được phép có ít hơn t-1 số tối thiểu của các keys). Cũng giống như một thuật toán chèn đơn giản có thể phải sao lưu nếu một node trên đường dẫn đến nơi keys được chèn vào đầy đủ, một cách tiếp cận đơn giản để xóa có thể phải sao lưu nếu một node (khác với gốc) dọc theo đường dẫn đến nơi key được xóa sẽ có số keys tối thiểu.
Delete method xóa k khỏi cây con được bắt nguồn từ x. Method này đảm bảo rằng bất cứ khi nào nó tự gọi mình một cách đệ quy trên một nút x, số keý trong x ít nhất là mức tối thiểu t. Lưu ý rằng điều kiện này đòi hỏi một keys quan trọng hơn mức tối thiểu yêu cầu bởi điều kiện cây B thông thường, do đó đôi khi một keys có thể phải được di chuyển vào một child node trước khi đệ quy child đó. Điều kiện được tăng cường này cho phép chúng ta xóa một key cây mà không cần phải "sao lưu" (với một ngoại lệ, chúng ta sẽ giải thích). Bạn nên giải thích các đặc tả sau để xóa từ cây B với sự hiểu biết rằng nếu node gốc x trở thành node bên trong không có keys (tình huống này có thể xảy ra trong trường hợp 2c và 3b sau đó chúng ta xóa x, và x chỉ có con x .c1 trở thành gốc mới của cây, giảm độ cao của cây bằng một cây và bảo quản tài sản mà gốc của cây chứa ít nhất một keys (trừ khi cây trống).
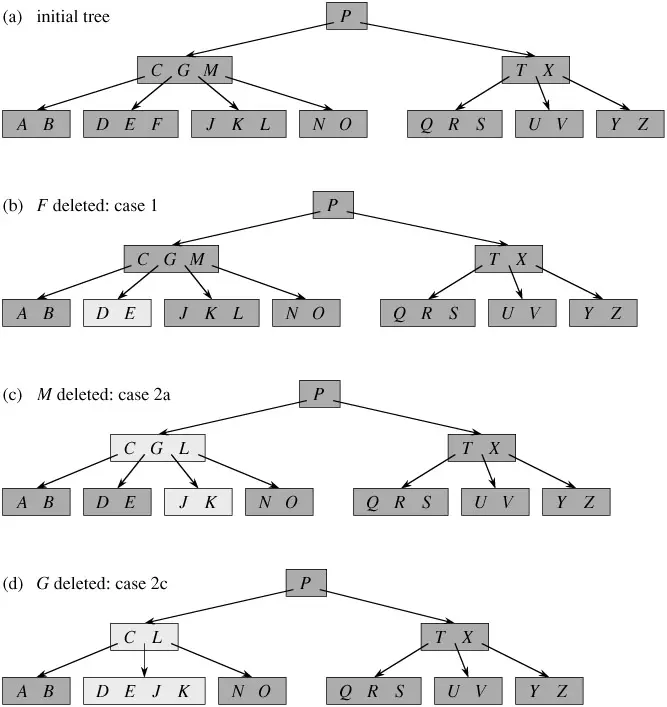
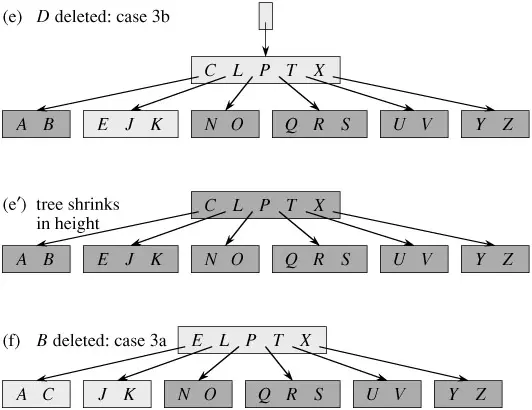
Để hiểu rõ hơn về các thuật toán sử dụng trong B-Trees cần có thêm tìm hiểu khác.
Cảm ơn và hi vọng bài viết có ích trong công việc của bạn.
All rights reserved