Mật mã RSA - phần 3
III. Mật mã RSA - thực hiện (tiếp)
4. Sinh số nguyên tố trong Python
Bước đầu tiên để tạo ra một cặp khóa public key và private key là lựa chọn cặp số nguyên tố , chúng sẽ đóng vai trò nền tảng cho tất cả các bước tạo khóa phía sau. Vậy thì, làm sao để tạo ra một cặp số nguyên tố ?
Ngày trước, khi không có sự hỗ trợ của các công nghệ tiên tiến, người xưa đã "lưu lại" các số nguyên tố bằng cách sử dụng sàng Eratosthenes: lần lượt bỏ đi các hợp số là bội của các số nguyên tố và cuối cùng chỉ giữ lại các số nguyên tố.

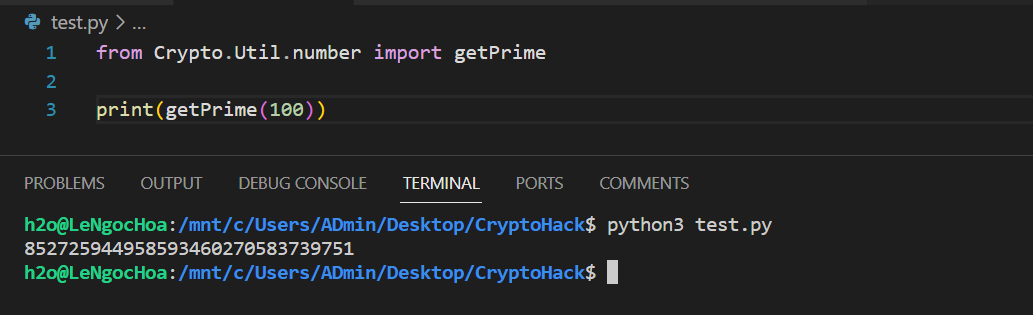
Với ngôn ngữ Python, có thể sử dụng hàm getPrime() trong module Crypto.Util.number thuộc thư viện PyCryptodome:
getPrime(N:int, randfunc:callable): long
Hàm sẽ trả về một số nguyên tố ngẫu nhiên có độ dài bytes.
5. Module trong Python
Như đã tìm hiểu ở bài trước, cách mã hóa và giải mã trong mật mã RSA phần lớn làm việc với các phép tính Module - đồng dư thức. Chẳng hạn những phép tính như tìm số dư của số trong module :
Trong Python có thể sử dụng hàm pow(base, exponent, modulus) kết hợp tính toán số mũ và đồng dư, tương đương với (base ** exponent) % modulus, trong đó:
baselà giá trị cơ số (số ).exponentlà giá trị số mũ (số ).moduluslà giá trị module (số ).
Ví dụ tính kết quả , chúng ta có chương trình đơn giản:
ans = pow(37, 18, 912)
print(ans)
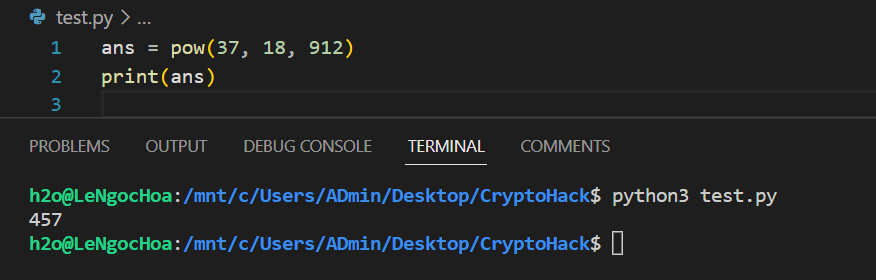
Ngoài ra, khi hàm pow() không nhận argument thứ ba modulus sẽ trở thành một hàm tính kết quả lũy thừa. Khi chương trình cần tính toán số lượng phép toán lũy thừa nhiều và dữ liệu lớn, có thể thay thế bằng hàm math.pow() sẽ cải thiện tốc độ đáng kể. Thật vậy, sử dụng module timeit thực hiện kiểm tra thời gian hai hàm:
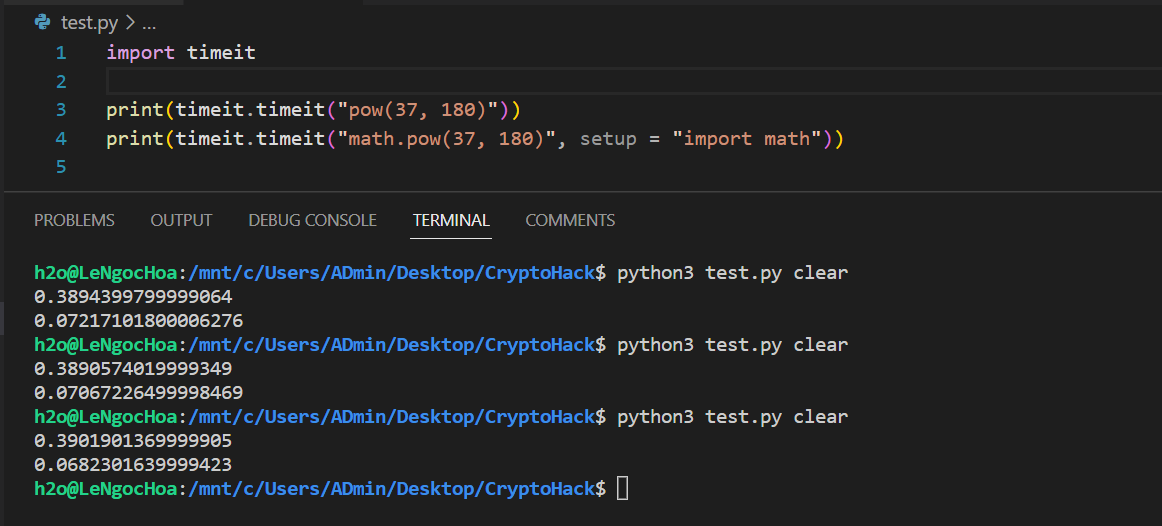
Có thể thấy ưu điểm vượt trội về thời gian của math.pow(), lý do là bởi vì khi chương trình được xử lý, hàm pow() sẽ tính toán dựa trên toán tử ** của Python, trong khi math.pow() dựa trên ngôn ngữ C cơ bản. Lưu ý rằng một nhược điểm của math.pow() không thể xử lý các số phức nhưng pow() có thể làm được điều đó, nên bạn đọc có thể cân nhắc sử dụng từng hàm trong mỗi trường hợp. Tham khảo thêm về bảng so sánh giá trị độ phức tạp thời gian và không gian:
| Method | Time Complexity | Space Complexity |
|---|---|---|
| Looping Technique | O(n) | O(1) |
** Operator |
O(Log(exponent)) | O(1) |
pow() function |
O(Log(exponent)) | O(1) |
math.pow() function |
O(1) | O(1) |
Quay lại bài tập ở phần trước: Với khóa công khai và , thông điệp mã hóa , số mũ bí mật hãy tìm ra thông điệp gốc ? Chúng ta có thể giải quyết dễ dàng bằng chương trình Python:
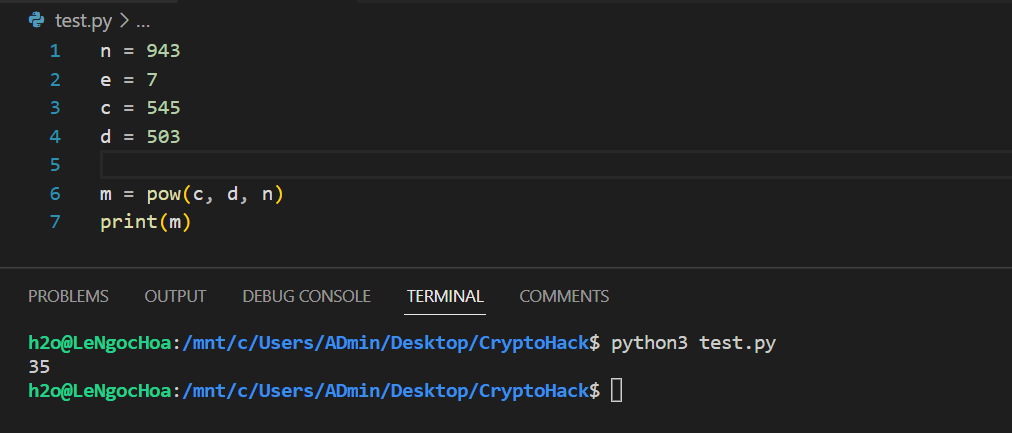
Bài tập dành cho bạn đọc: Cho cặp số nguyên tố , số mũ công khai , hãy mã hóa số .
6. Số nghịch đảo module - bài toán nghịch đảo module (Modular multiplicative inverse)
Khóa bí mật với số mũ bí mật cũng cần xác định nhằm giải mã thông điệp RSA.
Như chúng ta đã biết về cách xác định số mũ bí mật :
Việc từ phương trình module này tìm ngược lại số còn được gọi là bài toán nghịch đảo module:
Trước hết chắc hẳn cần trả lời cho câu hỏi: Nếu biết trước cặp khóa công khai , tức giá trị , đã biết thì có tồn tại thỏa mãn phương trình trên không? Câu trả lời là có, chúng ta có thể dễ dàng chứng minh dựa vào mệnh đề: Nếu thì luôn tồn tại các số nguyên sao cho:
Quay lại phương trình module trên, do nên ta luôn tìm được số nguyên (chọn dương) sao cho:
Chọn chính là giá trị cần tìm, chứng tỏ phương trình nghịch đảo module trên luôn giải được. Tiếp theo chúng ta cần giải quyết bài toán cách thức tìm ra .
Một cách đơn giản nhất đó là sử dụng vòng lặp thử tất cả trường hợp của bắt đầu từ , cho đến khi tìm được giá trị thỏa mãn phương trình module trên.
Xét ví dụ bài tập ở phần trước: Với khóa công khai và , thông điệp mã hóa , hãy tìm ra thông điệp gốc ? Chúng ta cần tìm được số mũ bí mật khi biết . Trước hết, có , nên . Chương trình tìm ra bằng cách thử tất cả trường hợp:
n = 943 # 943 = 23 x 41
p, q = 23, 41
e = 7
phi = (p-1) * (q-1)
# Thử tất cả trường hợp của d
d = 1
while True:
if (d * e - 1) % phi == 0:
print(d)
break
d = d + 1
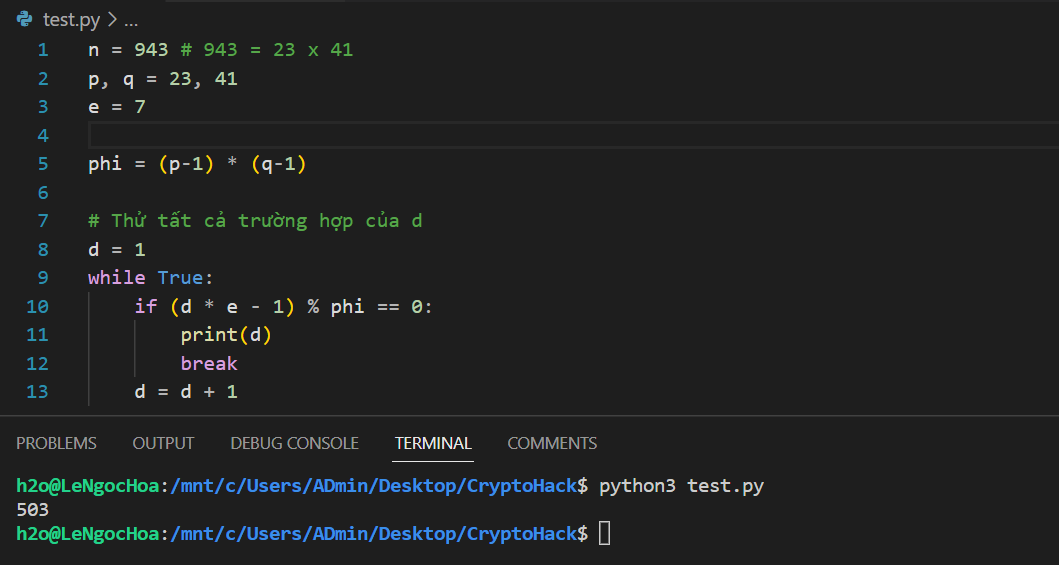
Tuy nhiên, việc sử dụng vòng lặp thử dần từng trường hợp của bắt đầu từ thực sự gặp khó khăn với số lớn. Chẳng hạn, với cặp số , chương trình có thể mất lượng thời gian rất lớn cho việc tìm ra khi mỗi vòng lặp chỉ tăng lên một đơn vị. Thay vào đó, chúng ta có thể tận dụng hàm pow() với exponent=-1 vì .
d = pow(e, -1, phi)
Áp dụng với cặp số nguyên tố lớn trên và , có thể nhanh chóng tính được số mũ bí mật :
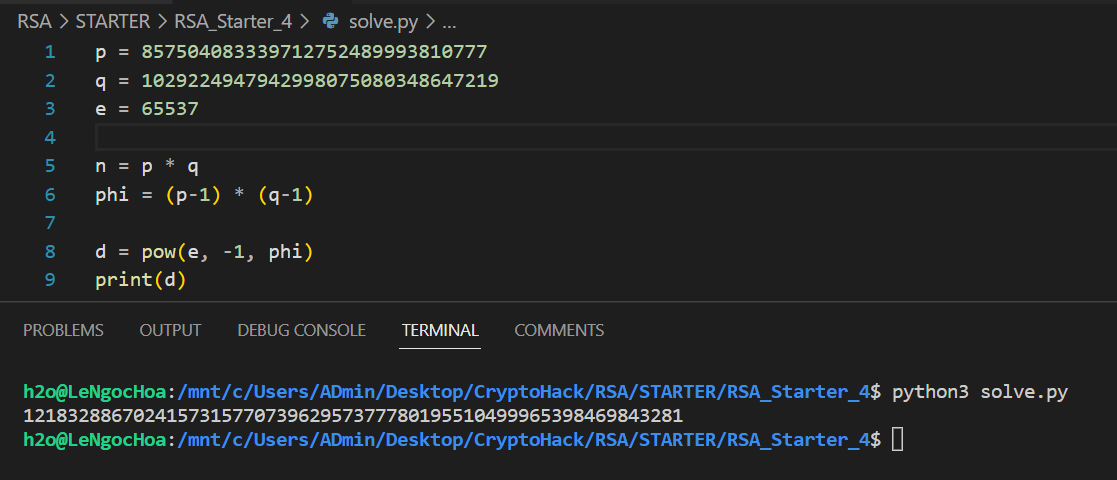
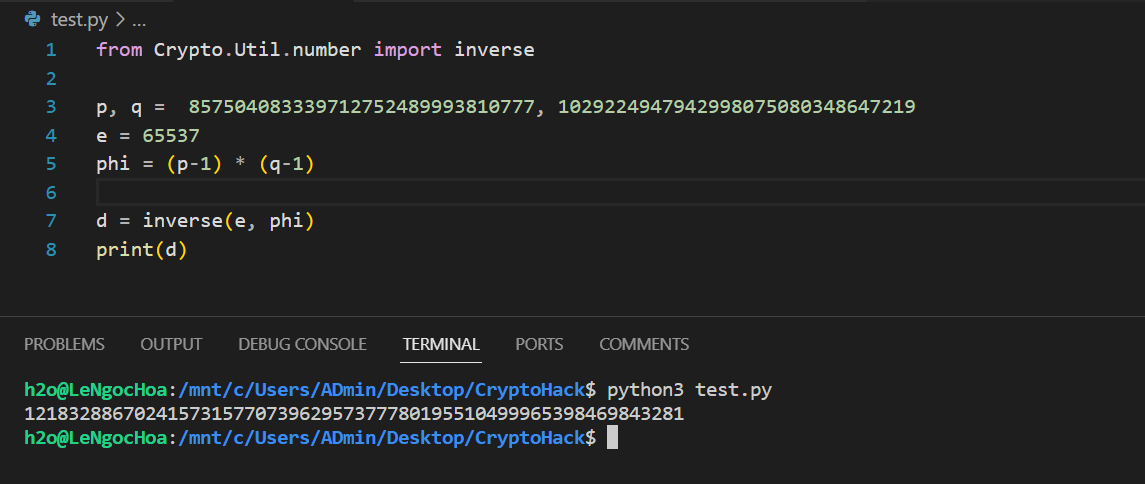
Bên cạnh đó, module Crypto.Util.number cũng chứa hàm inverse() hỗ trợ tìm kiếm số nghịch đảo module của số .
inverse(u:long, v:long): long
IV. Một số kỹ thuật tấn công n - phân tích số lớn ra tích hai thừa số nguyên tố
Trong mật mã RSA, chỉ có hai yếu tố được công khai là cặp số public key . Khi attacker muốn giải mã được thông điệp mã hóa , họ buộc phải đồng thời có được số mũ bí mật và . Trong phần này chúng ta sẽ tập trung vào các phương pháp tìm ra , hay nói cách khác, cần tìm ra cặp số nguyên tố , tức là giải quyết bài toán phân tích số ra tích hai thừa số nguyên tố.
1. Vấn đề khi lựa chọn cặp số nguyên tố nhỏ
Trước khi nói đến vấn đề an toàn, việc lựa chọn cặp số nguyên tố nhỏ sẽ dẫn tới nhỏ. Mật mã RSA được thực hiện dựa trên các phép toán module, nên chỉ có thể mã hóa thông điệp (sau khi chuyển đổi sang dạng dãy chữ số) nằm trong khoảng từ tới (Trong trường không gian module của ). Thật vậy:
Xét trường hợp mật mã RSA có khóa công khai , số mũ bí mật , chúng ta thử mã hóa một thông điệp lớn hơn khoảng module cho phép, . Ciphertext thu được:
Khi giải mã ngược lại:
Người nhận sẽ không thể tính ra chính xác thông điệp ban đầu, dẫn tới truyền tin thất bại. Như vậy, tích cặp số nguyên tố chọn ban đầu càng lớn, thì không gian thông điệp có thể mã hóa và truyền tải càng lớn.
Bên cạnh đó còn là vấn đề an toàn của mật mã, khi chọn cặp số nguyên tố sinh khóa nhỏ thì tỉ lệ bị attacker dựa vào khóa công khai tìm ra bộ số nguyên tố ban đầu là rất cao. Tính tới thời điểm , RSA với số có độ dài bit đã bị phân tích thành công (bạn đọc có thể tham khảo thêm tại đây).
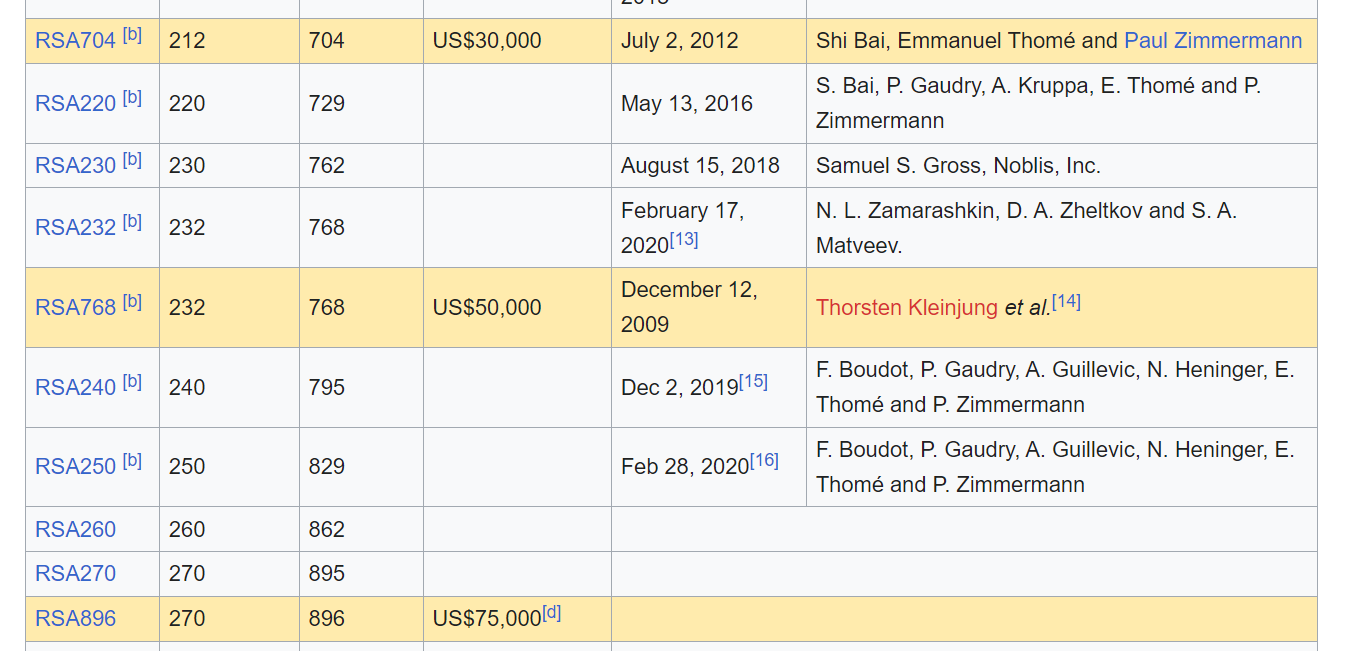
Trong bối cảnh CTF, khi gặp challenge có số nhỏ, người chơi có thể dễ dàng phân tích thành tích các thừa số nguyên tố bằng nhiều cách. Chẳng hạn với số dài bit. Một số nền tảng online hỗ trở phân tích thành thừa số nguyên tố:
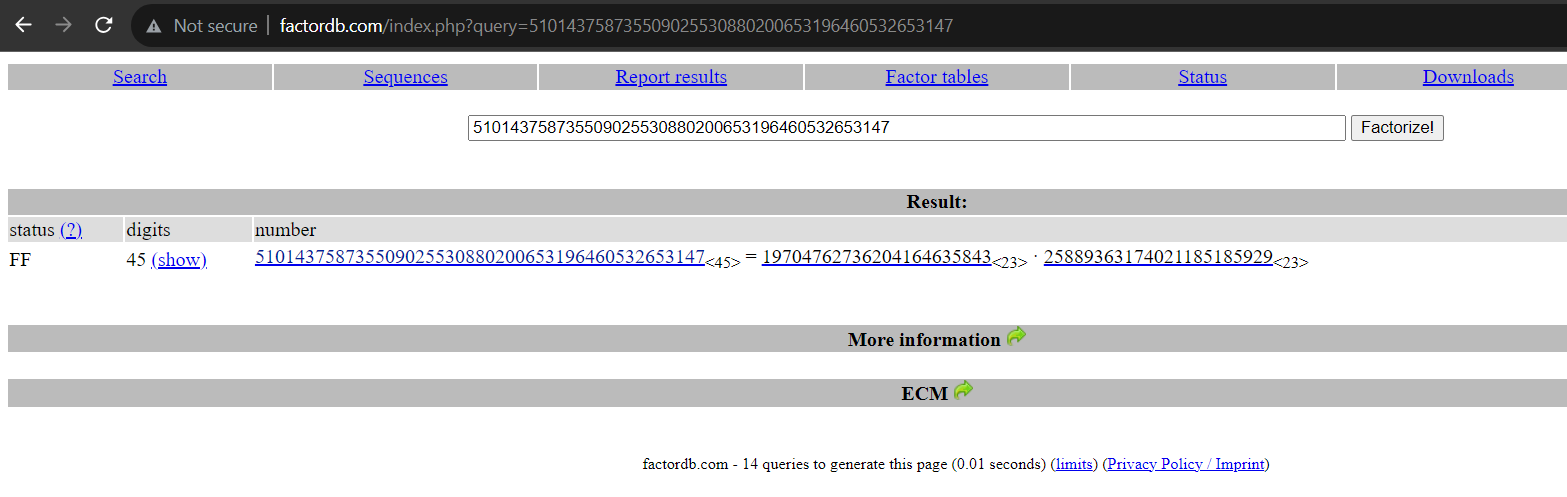
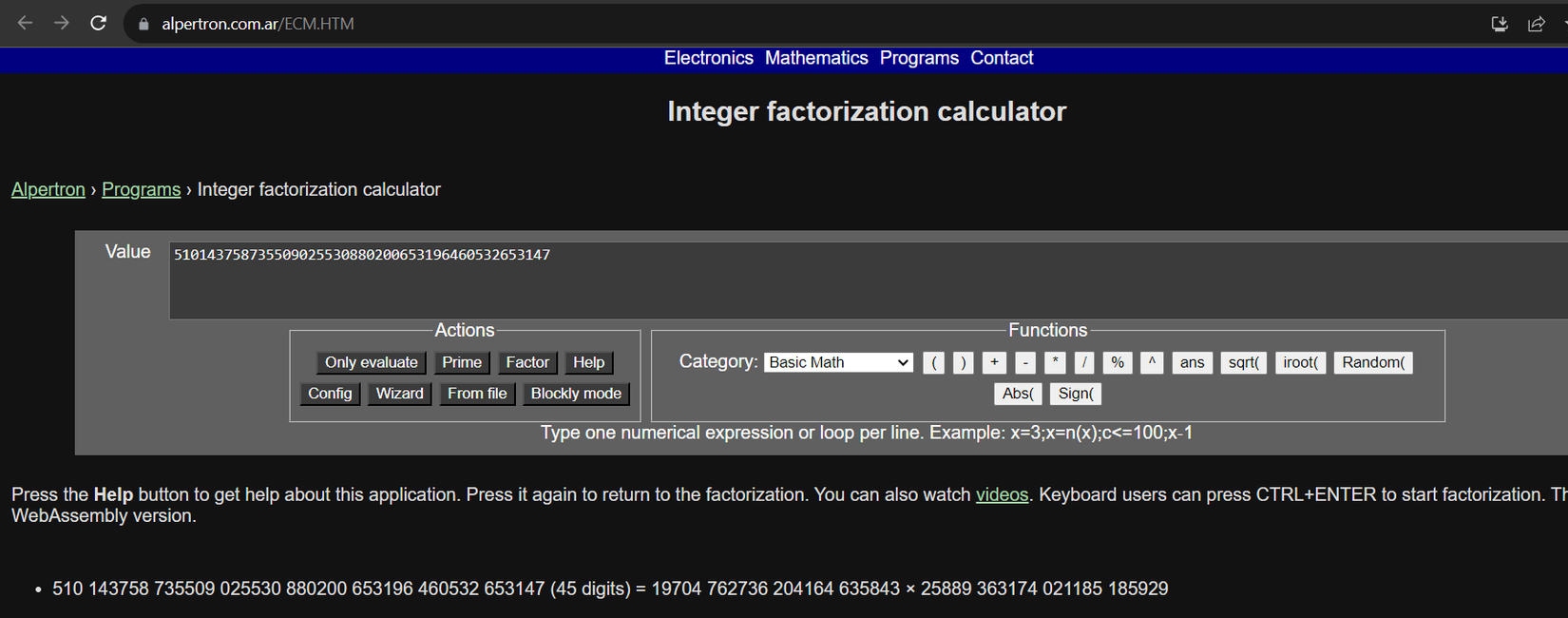
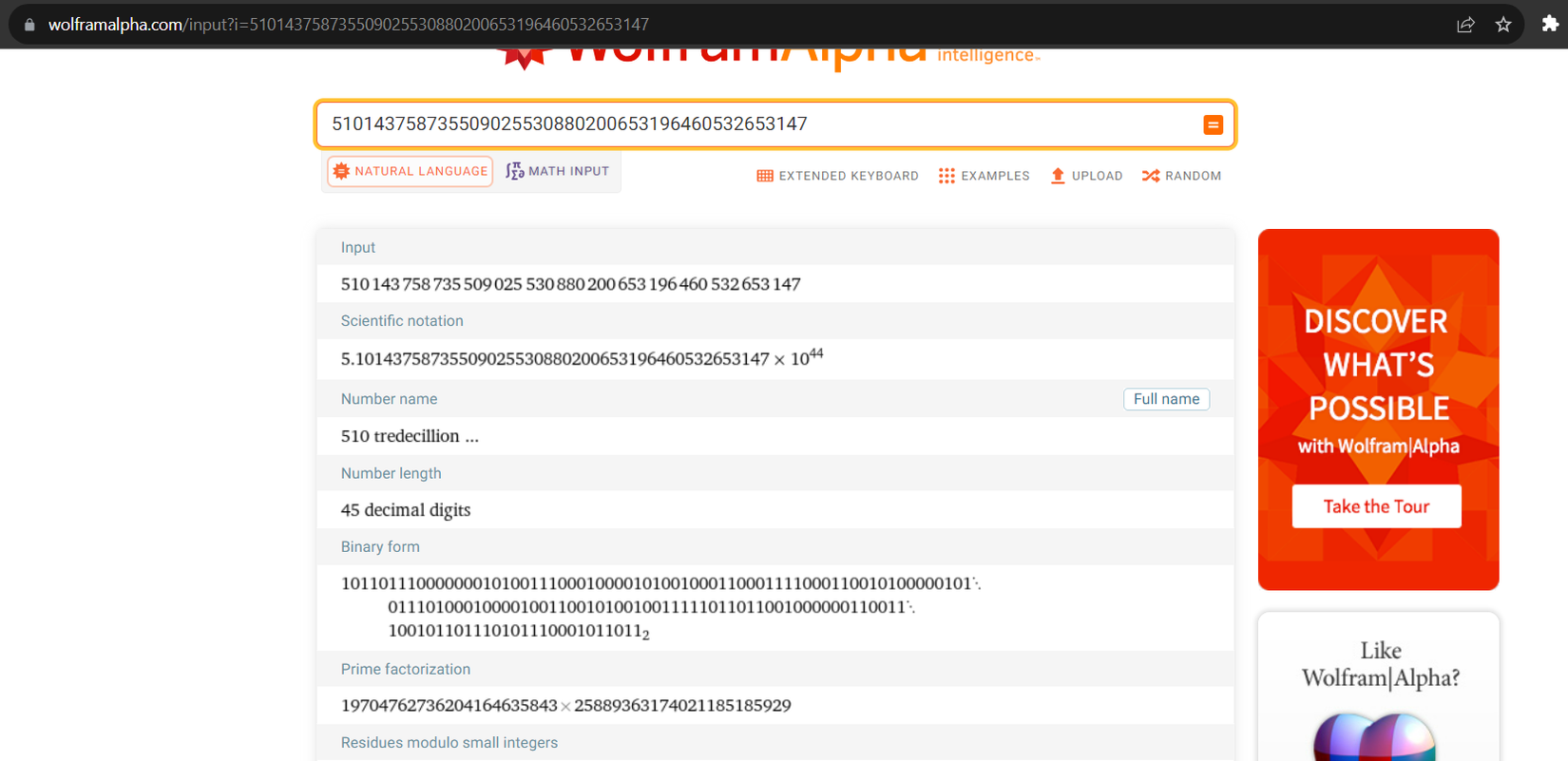
Bạn đọc có thể sử dụng một trong số các website factor online trên để giải quyết challenge Inferius Prime.
Tài liệu tham khảo
- https://en.wikipedia.org/wiki/RSA_(cryptosystem)
- https://www.amsi.org.au/teacher_modules/pdfs/Maths_delivers/Encryption5.pdf
- https://sites.math.washington.edu/~morrow/336_09/papers/Yevgeny.pdf
- https://vi.wikipedia.org/wiki/Giải_thuật_Euclid_mở_rộng
- https://en.wikipedia.org/wiki/RSA_Factoring_Challenge
- https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes
All rights reserved