MẬT MÃ KHÓA CÔNG KHAI
Bài đăng này đã không được cập nhật trong 5 năm
1. Tổng quan về mật mã công khai
Việc giữ bí mật khóa mật đồng nghĩa với việc giữ mật thông tin. Nên việc trao đổi khóa chỉ diễn ra trên kênh mật thì mới đảm bảo được, thế nhưng việc trao đổi này cung không phải dễ để đảm bảo độ an toàn cao. Từ đây hình thành nên ý tưởng của mật mã công khai. Tức là không cần phải trao đổi khóa mật qua kênh nữa.
Ý tưởng của hệ mật công khai được Diffie và Hellman đưa ra năm 1976. Còn việc thực hiện hệ mật công khai thì do Rivest, Shamir và Adleman đưa ra đầu tiên năm 1977, họ đề xuất một hệ mật RSA nổi tiếng. Và kể từ đó có một số hệ mật khác được công bố, độ mật của chúng dựa trên bài tính toán khác nhau, như dựa trên độ khó của bài toán phân tích thành nhân tử như hệ mật RSA, dựa vào độ khó logarithm rời rạc như hệ mật ElGamal, hay dựa trên đường cong Elliptíc. Chúng ta đi tìm hiểu cụ thể các hệ mật này trong các phần sau. Nhưng trước tiên chúng ta đi tìm hiểu sơ đồ và nguyên tắc mã và giải mã của hệ mật công khai.
Sơ đồ của hệ mã công khai được cho ở hình sau:
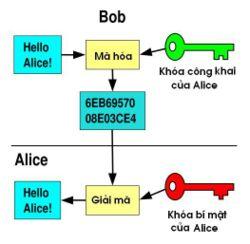
Hệ mã công khai sử dụng hai khóa có quan hệ toán học với nhau, tức là một khóa này được hình thành từ khóa kia: Người muốn nhận bản mã (Alice) tạo ra một khóa mật (private key) và từ khóa mật tính ra khóa công khai (public key) với một thủ tục không phức tạp, còn việc tìm khóa mật khi biết khóa công khai là bài toán khó giải được. Khóa công khai sẽ đưa đến cho người gởi bản tin (Bob) qua kênh công cộng. Và bản tin được Bob mã hóa bằng khóa công cộng. Bản mã truyền đến Alice, và nó được giải mã bằng khóa mật.
2. Hệ mật RSA
a. Lịch sử hình thành
Thuật toán được Ron Rivest, Adi Shamir và Len Adleman mô tả lần đầu tiên vào năm 1977 tại Học viện Công nghệ Massachusetts (MIT). Tên của thuật toán lấy từ 3 chữ cái đầu của tên 3 tác giả. Đây là thuật toán đầu tiên phù hợp với việc tạo ra chữ ký điện tử đồng thời với việc mã hóa. Nó đánh dấu một sự tiến bộ vượt bậc của lĩnh vực mật mã học trong việc sử dụng khóa công cộng. RSA đang được sử dụng phổ biến trong thương mại điện tử và được cho là đảm bảo an toàn với điều kiện độ dài khóa đủ lớn.
Thuật toán RSA được MIT đăng ký bằng sáng chế tại Hoa Kỳ vào năm 1983 (Số đăng ký 4,405,829). Bằng sáng chế này hết hạn vào ngày 21 tháng 9 năm 2000. Tuy nhiên, do thuật toán đã được công bố trước khi có đăng ký bảo hộ nên sự bảo hộ hầu như không có giá trị bên ngoài Hoa Kỳ. Ngoài ra, nếu như công trình của Clifford Cocks đã được công bố trước đó thì bằng sáng chế RSA đã không thể được đăng ký.
Thuật toán dựa trên độ khó của bài toán phân tích một số thành nhân tử.
b. Quá trình tạo khóa cho hệ mật RSA.
Giả sử Alice và Bob cần trao đổi thông tin bí mật thông qua một kênh không an toàn (ví dụ như Internet). Với thuật toán RSA, Alice đầu tiên cần tạo ra cho mình cặp khóa gồm khóa công khai và khóa bí mật theo 6 bước sau:

Quá trình mã hóa:

Quá trình giải mã:

c. Một số chú ý quan trọng về RSA
An ninh: Độ an toàn của hệ thống RSA dựa trên 2 vấn đề của toán học: bài toán phân tích ra thừa số nguyên tố các số nguyên lớn và bài toán RSA. Nếu 2 bài toán trên là khó (không tìm được thuật toán hiệu quả để giải chúng) thì không thể thực hiện được việc phá mã toàn bộ đối với RSA. Phá mã một phần phải được ngăn chặn bằng các phương pháp chuyển đổi bản rõ an toàn. Bài toán RSA là bài toán tính căn bậc e môđun n (với n là hợp số): tìm số m sao cho me=c mod n, trong đó (e, n) chính là khóa công khai và c là bản mã. Hiện nay phương pháp triển vọng nhất giải bài toán này là phân tích n ra thừa số nguyên tố. Khi thực hiện được điều này, kẻ tấn công sẽ tìm ra số mũ bí mật d từ khóa công khai và có thể giải mã theo đúng quy trình của thuật toán. Nếu kẻ tấn công tìm được 2 số nguyên tố p và q sao cho: n = pq thì có thể dễ dàng tìm được giá trị (p-1)(q-1) và qua đó xác định d từ e. Trong chương số học chúng ta đã biết chưa có một phương pháp nào được tìm ra trên máy tính để giải bài toán này trong thời gian đa thức (polynomial-time). Tuy nhiên người ta cũng chưa chứng minh được điều ngược lại (sự không tồn tại của thuật toán).
Tốc độ: RSA có tốc độ thực hiện chậm hơn đáng kể so với các thuật toán mã hóa đối xứng. Trên thực tế, Bob sử dụng một thuật toán mã hóa đối xứng nào đó để mã hóa văn bản cần gửi và chỉ sử dụng RSA để mã hóa khóa để giải mã (thông thường khóa ngắn hơn nhiều so với văn bản). Phương thức này cũng tạo ra những vấn đề an ninh mới. Một ví dụ là cần phải tạo ra khóa đối xứng thật sự ngẫu nhiên. Nếu không, kẻ tấn công (thường ký hiệu là Eve) sẽ bỏ qua RSA và tập trung vào việc đoán khóa đối xứng.
Chiều dài khóa: Số n cần phải có kích thước không nhỏ hơn 512 bít. Năm 2006 hệ mật RSA được cho là hiệu quả với kích thước n phải từ 1024. Và họ khuyến cáo là tương lai thì chiều dài n phải từ 2024 bít.
Chọn tham số công khai:
Để nâng cao tốc độ mã hóa, thì chúng ta nên chọn e với giá trị không lớn, thường là 3, 7 hay 65537. Các số này khi biểu diễn ở dạng nhị phân chỉ có 2 chữ số 1, nên khi thực hiện lệnh lũy thừa sẽ giảm đi lệnh nhân.
Chọn tham số mật.


3. Hệ mật Elgama
Hệ mật Elgama hình thành trên cơ sở bài toán logarith rời rạc. Được đề xuất năm 1984. Sau đó chuẩn chữ ký điện tử của Mỹ và Nga hình thành trên cơ sở hệ mật này.
a. Hình thành khóa:

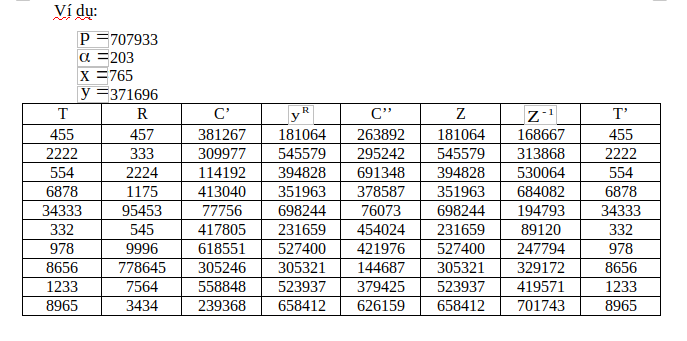
b. Quá trình mã hóa bản tin T:

c. Quá trình giải mã:

4. Hệ mật Rabin
Đây là hệ mật dựa trên độ phức tạp của việc tính căn bậc hai theo hợp số. Đây là hệ mật có độ an toàn về mặc tính toán chống lại được tấn công bản rõ lựa chọn và không có khả năng phân tích được n=pq. Thuật toán được ứng dụng rất nhiều trong thực tế.
a. Thuật toán hệ mật Rabin
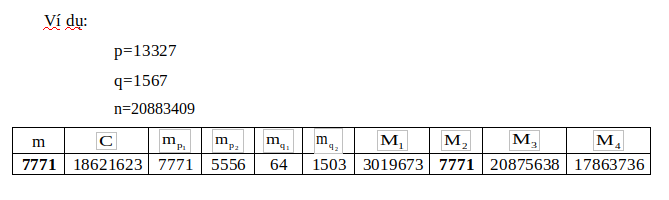
Quá trình tạo khóa:

Quá trình mã hóa:
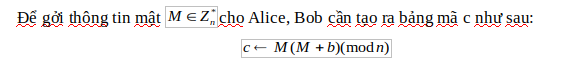
Qúa trình giải mã:
 Chúng ta chứng minh thuật toán xxx này là một hệ mật, có nghĩa là quá trình giải mã được thực hiện bởi Alice sẽ khôi phục lại bản rõ được mã hóa bới Bob.
Chúng ta chứng minh thuật toán xxx này là một hệ mật, có nghĩa là quá trình giải mã được thực hiện bởi Alice sẽ khôi phục lại bản rõ được mã hóa bới Bob.
Giải phương trình bậc 2, chúng ta có nghiệm chung dạng:



5. Hệ mật Merkle-hellman
Hệ mật xếp ba lô Merkle-hellman được Merkle-hellman miêu tả năm 1978. Hệ mật này bị phá vở năm 1980, sau đó có một số biến thể của nó ra đời. Mặc dầu nó bị phá nhưng nó cho chúng ta thấy một sự tinh tế trong thiết kế hệ mật. Bài toán này dựa trên bài toán tổng các tập con. Bài toán được phát biểu như sau
a. Bài toán về tổng các tập con.

Dựa trên thực giải này Merle-Hellman đi xây dựng thuật toán của mình. Ý tưởng thuật toán là, dùng dãy siêu tăng để giải mã, và giải mã bằng một dãy không phải siêu tăng, tức là dãy siêu tăng đóng vai trò là khóa mật, còn dãy không siêu tăng đóng vai trò là khóa công cộng. Từ đây họ đưa ra cách để biến dãy siêu tăng thành dãy không có tính đó, và việc tìm dãy siêu tăng theo khóa công cộng là bài toán khó. Một cách biến đổi mà Merle-Hellman nêu ra là biến đổi dãy siêu tăng theo modulo nguyên tố p, sao cho:

b. Hệ mật Herkle-Hellman

Quá trình mã hóa:
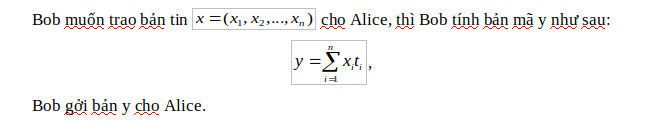
Quá trình giải mã.

6. Hệ mật McEliece
Hệ mật McEliece được đề xuất năm 1978, tác giả của nó là Robert McEliece. Ý tưởng của bài toán này giống với ý tưởng của hệ mật Merkle-Hellman: Phép giải mã là trường hợp đặc biệt của bài toán NP đầy đủ.
Để hiểu được hệ mật này các bạn phải nắm được kiến thức cơ bản về lý thuyết cơ bản về truyền tin, thông tin.

a. Quá trình hình thành khóa:

b. Quá trình mã hóa:

c. Quá trình giải mã:




7. Hệ mật bất đối xứng trên cơ sỡ đường cong Elliptic

a. Quá trình mã hóa:

b. Quá trình giải mã:
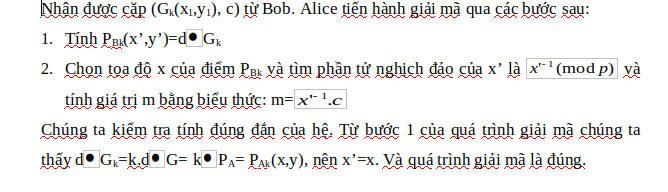
All rights reserved