Giới Thiệu

Việc lưu trữ và cất giấu bảo mật thông tin hiện nay là một nhu cầu tất yếu. Ta có thể mã hóa thông tin cần bảo mật theo một cách thức nào đó như mã hóa RSA, DES,... Nhưng việc mã hóa này lại đẫn đến một hệ quả đó chính là có thể dễ dành phát hiện ra thông tin bị mã hóa và kể tấn công sẽ có thể dễ dàng xác định được mục tiêu cần tấn công. Từ đó ta có một hướng tiếp cận khác là ta sẽ ẩn giấu thông tin cần an toàn trong một số loại tài nguyên thông dụng như ảnh, âm thanh, hay video và trao đổi qua lại mà khó bị kẻ tấn công phát hiện ra có thông tin giấu trong chúng.

Thuật toán Chen-Pan-Tseng là 1 thuật toán được dùng để giấu một chuỗi bít vào một ma trân nhị phân cấp MxN sao cho chỉ cần thay đổi tối đa 2 bít ở trên ma trận. Từ đó ta có thể phát triển thành việc giấu 1 chuỗi bí mật vào trong 1 bức ảnh đen trắng chỉ gồm các pixel 0 và 1 mà bức ảnh này không bị thay đổi quá nhiều và khó phân biệt bằng mắt thường.

Về Thuật toán

Đầu vào của thuật toán: - F là một ma trận ảnh gốc dùng để giấu thông tin. F được chia thành các khối Fi, mỗi ma trận điểm ảnh Fi có kích thước là mxn, để cho đơn giản ta giả sử rằng F là bội của các Fi. - K là một ma trận khóa cấp mxn. - W là một ma trận trọng số cấp mxn. - r: Số lượng bit sẽ nhúng trong mỗi một khối ảnh mxn. - B : là lượng thông tin cần giấu gồm k*r bít, k sẽ là số khối ảnh giấu. - Ta có thể thấy rằng việc chọn w với MxN đủ lớn sẽ có vô số khả năng nên việc dùng brute-force để phá giải là rất khó và đòi hỏi lượng tài nguyên cực lớn.

Đầu ra của thuật toán: - Ảnh đích F‟ chứa B. F‟ được tạo từ các khối Fi‟, Mỗi Fi‟ thu được từ khối Fi tương ứng sau khi đã giấu r bit thông tin từ B.

• Bước 1: Tính ma trận T=Fi (XOR) K
  Tính ma trận P = TxW
• Bước 2: Tính tổng Sum = SUM(P)
• Bước 3: Với ma trận T và với mọi w=1,2,…,2r-1 ta xác định tập hợp Sw như sau:

Sw={(j,k)|(W[i,j]=wT[i,j]=0) ν (W[j,k] =2r –wT[j,k]=1)} 

Dễ nhận thấy Sw là tập hợp các tọa độ (i,k) của ma trận Fi sao cho khi đảo bít Fi[i,j] thì Sum ở bước hai tăng lên w đơn vị. Thực vậy, ta có: -Trường hợp 1: Nếu W[i,j]=w và T[i,j]=0
Khi đó đảo bit Fi[i,j] sẽ làm cho T[j,k]=1, do đó Sum tăng lên w. -Trường hợp 2: Nếu W[j,k] =2r –w và T[j,k]=1
Khi đó đảo bit Fi[i,j] sẽ làm T[i,j]=0, do đó Sum sẽ giảm đi 2r-1-w, tức là tăng lên w theo mod 2r.
Từ định nghĩa của tập Sw ta có:
Sw‟ =Sw

• Bước 4: Ký hiệu d=(b1b2...br) –SUM(P)(mod2r).
  Ta cần thực hiện việc đảo bit trên Fi để được Fi‟ sao cho tổng Sum tính được ở bước 2 khi thay Fi bởi Fi‟ sẽ tăng lên d.
  - Nếu d=0, không cần thay đổi Fi
  - Nếu d 0 ta thực hiện các công việc sau:
  1) Chọn h bất kỳ thuộc tập {1,2,3…,2r-1} sao cho Shd và S-(h-1)d
  2) Chọn phần tử (j,k) bất kỳ thuộc Shd và đảo bit Fi[j,k]
  3) Chọn phần tử (u,v) bất kỳ thuộc S-(h-1)d và đảo bít Fi[u,v]
  Rõ ràng là để tăng Sum lên d, ta có thể chọn hai tập khác trống Shd và S-(h-1)d. Thật vậy, hai tập này chứa các vị trí bit trong khối Fi mà ta có thể đảo để
  tăng Sum lên dh và –(h-1)d một cách tương ứng, kết quả cuối cùng là Sum sẽ tăng lên hd+(-(h-1)d) =d;
  Tương tự như các tập Sw khác ta cũng có thể coi tập S0 là tập chứa các vị trí mà khi đảo những bít có vị trí này trên Fi, thì sẽ tăng Sum lên 0. Kết quả này cũng đạt được nếu ta không đảo bất kỳ bit nào trên Fi. Vì vậy, ta có thể coi S0 là tập trống và khi nói đảo 1 bit có vị trí thuộc tập S0 có nghĩa là không cần làm gì cả.
  

Ví dụ:

Giả sử ta có một ma trận ảnh F 8x8 được chia thành 4 ma trận khối ảnh F1, F2, F3, F4 cùng cỡ 4x4, một ma trận khóa K 4x4 và một ma trận cùng cỡ như sau: Ma trận ảnh F8x8

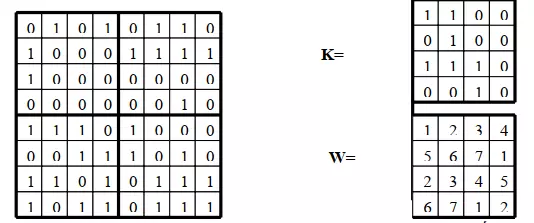
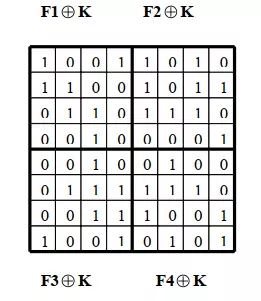
Trong ví dụ này, ta đã chọn m = n = 4. chọn r=3 ta giấu 12 bit sau B=001010000001 vào trong ảnh F. Như vậy, đoạn bit 001 sẽ được giấu vào khối F1,010 sẽ được giấu vào khối F2, 000 sẽ được giấu vào khối F3, 001 trong F4. Bước 1: Ta thực hiện phép toán XOR của Fi với K. Kết quả cho trong bảng sau:

Bước 2: Ta thực hiện phép nhân từng khối ma trận kết quả trên với ma trận trọng số:

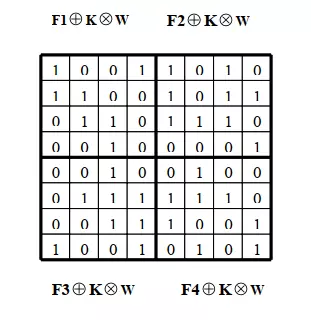
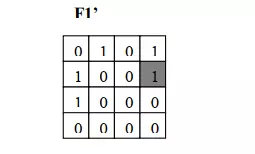
Với F1: Lưu ý rằng ta có 23 =8. Tính SUM(F1 K W)=0(mod 8). Vì chuỗi ba bit cần giấu đầu tiên là 001 nên ta sẽ phải thay đổi để tăng trọng số lên 1 (d = 1) Ta xây dựng tập S1: h=1 : S1 ={(2,2)} ta chọn luôn ô này để đảo bít. Khi đó ma trận khối ảnh F1‟ là:

Với F2: Tính SUM(F2 K W)=2(mod8). Và vì chuỗi 3 bit tiếp theo cần giấu là 010=2 nên không cần phải thay đổi F2 nữa. Với F3: Tính SUM(F3 K W)= 2(mod 8). Và vì 3 bit tiếp theo cần giấu là 000=0 nên ta cần thay đổi F3 để tăng trọng số lên d=6. Ta cần xây dựng tập S6 h=1: S6 ={(4,4)} ≠ ta chọn luôn ô này để đảo bit. Khi đó ma trận khối ảnh là:

Với F4: Tính SUM(F4 K W)=4 (mod 8). Vì ba bit cần giấu tiếp theo là 001=1 nên ta sẽ thay đổi để tăng trọng số lên 5, (d=5) Ta xây dựng tập S5: h=1 : S5= h=2: S10=S2={(2,2)}. S(-5)={(1,3),(2,1),(3,2),(3,4)} Ta chọn đảo bit ở hai ô [F4]2,2 và [F4]3,2. Khi đó ma trận khối ảnh là:

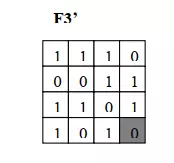
Ảnh tạo thành ma trận ghép 4 khối điểm ảnh F1‟, F2‟, F3‟, F4‟

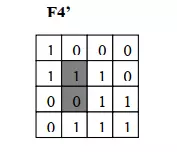
Như vậy ta đã giấu xong thông tin B vào trong các khối theo thuật toán.

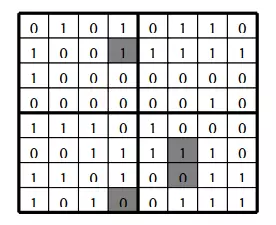
Kết quả thực tế

Đây là 2 bức ảnh đã được giấu tin 1 chuỗi bí mật vào và dùng mắt thường gần như là rất khó phát hiện ra sự sai khác giữa 2 bức ảnh.

Lời kết

Qua bài viết mình đã trình bày cho mọi người về kĩ thuật giấu tin CPT. Các bạn quan tâm có thể tham khảo project demo do mình phát triển tại link sau: https://github.com/lkintheend/cptalgo Project này mình sử dụng ngôn ngữ java với ảnh đầu vào là ảnh hình vuông 2bit-color. Thanks!