High Performance Python - Lists and Tuples (Part I)

Nếu các bạn tìm đến bài viết này tức là bạn đã viết ra được những chương trình chạy đúng và hiện tại bạn đang muốn cải thiện hiệu năng cho những chương trình đó.

Hiện tại tôi đang đọc cuốn sách tên High Performance Python của hai tác giả Micha Gorelick và Ian Ozsvald. Có một số phần tôi thấy khá hay và dễ hiểu nên tôi quyết định sẽ chọn những phần này để dịch và truyền tải đến các bạn.

Chương 3 của cuốn sách nói về Lists và Tuples trong Python.

Một trong những điều quan trọng để viết ra các chương trình hiệu quả chính là việc thấu hiểu được giá trị của các cấu trúc dữ liệu mà bạn sử dụng. Trong thực tế, một phần quan trọng trong lập chương trình hiệu năng (performant programming) chính là hiểu câu hỏi nào mà bạn đang muốn hỏi về dữ liệu của bạn và chọn ra một cấu trúc dữ liệu có thể trả lời những câu hỏi đó một cách nhanh chóng. Trong chương này, chúng ta sẽ bàn về các kiểu câu hỏi mà list và tuple có thể trả lời và cách chúng hoạt động.

List và tuple là một lớp cấu trúc dữ liệu gọi là array. Một array đơn giản là một danh sách dữ liệu phẳng (a flat list of data - nghĩa là không có cấp bậc) với một vài bộ sắp xếp thứ tự được cài đặt sẵn. Array có thể được implement theo nhiều cách khác nhau. Việc này phân định ranh giới giữa list và tuple: list là các array động (dynamic array) trong khi tuple là các array tĩnh (static array).

Hãy cũng làm rõ phát biểu bên trên một chút. Bộ nhớ hệ thống của máy tính có thể được coi như là một chuỗi các bucket được đánh số (numbered buckets), mỗi bucket có khả năng nắm giữ một con số. Những con số này có thể được biểu diễn bất cứ biến nào chúng ta quan tâm (integer, float, string hoặc các cấu trúc dữ liệu khác), bởi chúng đơn giản chỉ là tham chiếu đến vị trí mà dữ liệu được lưu trong bộ nhớ.

Khi chúng ta muốn tạo ra một array (một list hoặc tuple), đầu tiên chúng ta phải cấp phát một block bộ nhớ hệ thống (ở đó, mỗi section của block này sẽ được sử dụng như là một con trỏ cỡ integer (integer-sized pointer) trỏ đến dữ liệu thực). Một yêu cầu sử dụng N bucket liên tiếp sẽ được gửi đến kernel - tiến trình con (subprocess) của hệ điều hành. Hình 3-1 minh họa một ví dụ về việc bố trí bộ nhớ hệ thống cho một array (trong trường hợp này là một list) có kích thước 6. Chú ý rằng Python list lưu cả độ lớn của nó, vậy nên trong 6 block được cấp phát, chỉ có 5 là khả dụng - còn phần tử đầu tiên là giá trị length.

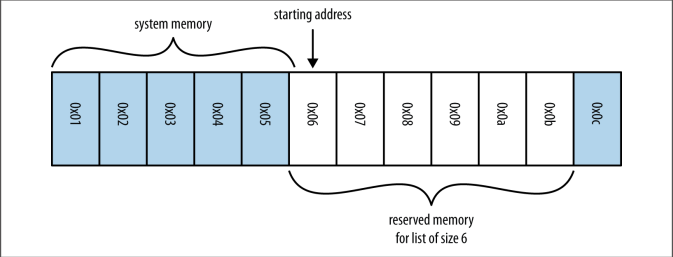
Hình 3-1. Ví dụ về việc bố trí bộ nhớ hệ thống cho một array kích thước 6

Để tìm kiếm một phần tử xác định trong list, chúng ta đơn giản chỉ cần biết phần tử chúng ta cần và nhớ bucket mà dữ liệu của chúng ta bắt đầu. Bởi vì tất cả dữ liệu chiếm cùng một lượng không gian (một bucket, hay chính xác hơn, một con trỏ cỡ integer trỏ đến dữ liệu thực), chúng ta không cần biết bất kiểu dữ liệu đang được lưu để thực hiện tính toán.

Câu hỏi: Nếu bạn biết vị trí mà list N phần tử của bạn được lưu thì làm cách nào bạn có thể tìm được một phần tử bất kỳ trong list?

Nếu, ví dụ, chúng ta cần lấy ra phần tử đầu tiên trong array, chúng ta đơn giản là đi đến bucket đầu tiên trong dãy bucket, M + 1 (trong cuốn sách ghi là M, có lẽ là họ nhầm lẫn một chút), và đọc ra giá trị của nó. Nếu, mặt khác, chúng ta cần phần tử thứ năm trong array, chúng ta sẽ đi đến bucket ở vị trí M + 5 và đọc giá trị. Nói chung, nếu chúng ta muốn lấy ra phần tử i trong array, chúng ta đi đến bucket M + i. Vậy, từ việc dữ liệu được lưu trong những bucket liên tục và biết được thứ tự của dữ liệu, chúng ta có thể định vị được dữ liệu của chúng ta trong một bước (O(1)) mà chẳng cần quan tâm đến độ lớn của array.

Ví dụ 3-1:

In [1]: %%timeit l = range(10)
   ...: l[5]
   ...:
10000000 loops, best of 3: 31.8 ns per loop

In [2]: %%timeit l = range(10000000)
   ...: l[1000000]
   ...:
The slowest run took 90.84 times longer than the fastest. This could mean that an intermediate result is being cached.
10000000 loops, best of 3: 31.7 ns per loop

Sẽ thế nào nếu chúng ta có một array nhưng không biết trước thứ tự và muốn lấy ra một phần tử xác định? Mọi thứ sẽ đơn giản nếu chúng ta biết trước được thứ tự của các phần tử trong array. Tuy nhiên, trong trường hợp này, chúng ta phải thực hiện một thao tác search. Cách tiếp cận đơn giản nhất đối với bài toán này chính là "linear search", ở đó chúng ta lặp từng phần tử trong array và kiểm tra xem chúng có phải là giá trị chúng ta cần hay không.

Ví dụ 3-2:

def linear_search(needle, array):
    for i, item in enumerate(array):
        if item == needle:
            return i
    return -1

Độ phức tạp của giải thuật này là O(n). Trường hợp xấu nhất xảy ra là khi chúng ta phải duyệt tới phần tử cuối cùng của array mới biết được array đó có chứa phần tử chúng ta cần hay không. Thực tế, đây chính cách người ta implement method list.index().

Cách duy nhất để tăng tốc độ tìm kiếm chính là nhờ những hiểu biết khác về cách dữ liệu được lưu trong bộ nhớ hoặc sự sắp xếp của các bucket dữ liệu chúng ta đang có. Ví dụ, hash table - một cấu trúc dữ liệu cơ bản tạo nên sức mạnh cho dictionary và set - giải quyết bài toán với thời gian O(1) mà không cần đếm xỉa đến thứ tự ban đầu của dữ liệu. Như một sự thay thế, nếu dữ liệu của bạn được sắp xếp theo cái cách mà mỗi phần tử lớn hơn (hoặc nhỏ hơn) so với hàng xóm (neighbour) ở bên trái (hoặc bên phải) thì các giải thuật tìm kiếm đặc trưng có thể được sử dụng để giảm thời gian tìm kiếm của bạn xuống còn O(log n). Việc giảm thời gian tìm kiếm xuống mức hằng số (constant-time) nghe có vẻ bất khả thi nhưng đôi khi đây là sự lựa chọn tốt nhất (đặc biệt bởi vì các giải thuật tìm kiếm linh động hơn và cho phép bạn định nghĩa việc tìm kiếm theo những cách sáng tạo).

Câu hỏi:
  Cho dữ liệu sau, hãy viết giải thuật để tìm index của giá trị 61:
    [9, 18, 18, 19, 29, 42, 56, 61, 88, 95]
  Do bạn biết dữ liệu được sắp xếp theo thứ tự, làm thế nào bạn có thể làm việc này nhanh hơn?
  Gợi ý: Nếu bạn chia đôi array, bạn biết tất cả các giá trị ở bên trái là nhỏ hơn phần tử nhỏ nhất của tập bên phải.

Một cách search hiệu quả hơn

Như ám chỉ trước đó, chúng ta có thể đạt được hiệu suất tìm kiếm tốt hơn nếu đầu tiên chúng ta sắp xếp dữ liệu sao cho tất cả các phần từ ở bên trái của một phần tử bất kỳ sẽ luôn nhỏ hơn (hoặc lớn hơn) nó. Việc so sánh được thực hiện thông qua các hàm __eq__ và __lt__.

Chú ý: Nếu không có __eq__ và __lt__, một object tùy biến (custom object) sẽ chỉ so sánh được với các object của kiểu và việc so sánh sẽ được thực hiện thông qua sự bố trí instance trong bộ nhớ.

Bên lề: Thực sự thì mình cũng chẳng biết dịch thế nào cho hợp lý. Và ban đầu thì mình cũng không hiểu cái đoạn "việc so sánh sẽ được thực hiện thông qua sự bố trí instance trong bộ nhớ" nghĩa là như thế nào. Hỏi thằng cu bên cạnh thì nó thử gõ một vài lệnh thì hóa ra là đối với các custom object mà không có method __eq__ hay __lt__, các object sẽ được so sánh với nhau dựa vào địa chỉ bộ nhớ. Ví dụ:

class A():
    # Some stuff about class A


class B():
    # Some stuff about class B

>>object_A = A()
>>object_B = B()

>>address_of_object_A = id(object_A)  # 56687912
>>address_of_object_B = id(object_B)  # 56687952

>>print((object_A > object_B) == (address_of_object_A > address_of_object_B))
True

Hai yếu tố thiết yếu chính là giải thuật sắp xếp và giải thuật tìm kiếm. Python list có một giải thuật sắp xếp có sẵn sử dụng Timsort. Trong trường hợp tốt nhất, thời gian sắp xếp là O(n); còn ngược lại, trong trường hợp tồi nhất là O(n log n).Hiệu năng này thu được nhờ việc sử dụng hỗn hợp nhiều giải thuật sắp xếp và sử dụng phương pháp phỏng đoán (heuristics) để chọn ra giải thuật tốt nhất với dữ liệu đã cho (cụ thể hơn, nó lai hóa các giải thuật tìm kiếm chèn (insertion) và trộn (merge)).

Một khi list đã được sắp xếp, chúng ta có thể tìm phần tử mong muốn sử dụng tìm kiếm nhị phân (Ví dụ 3-3) với độ phức tạp thuật toán là O(log n). Đầu tiên, giải thuật sẽ xét đến phần tử ở giữa list và só sánh giá trị của nó với giá trị mong muốn. Nếu giá trị của giá trị đó nhỏ hơn giá trị mong muốn, chúng ta sẽ xét đến nửa bên phải của list. Sau đó chúng ta tiếp tục chia đôi list giống như vậy cho đến khi giá trị được tìm thấy hoặc khi biết rằng phần tử mong muốn không tồn tại. Và như vậy, chúng ta không cần duyệt tất cả các giá trị trong list như khi làm việc với tìm kiếm tuyến tính. Thay vào đó, chúng ta chỉ phải xét một tập nhỏ các giá trị.

Ví dụ 3-2: Tìm kiếm nhị phân

def binary_search(needle, haystack):
    imin, imax = 0, len(haystack)
    while True:
        if imin >= imax:
            return -1
        midpoint = (imin + imax) // 2
        if haystack[midpoint] > needle:
            imax = midpoint
            elif haystack[midpoint] < needle:
            imin = midpoint + 1
        else:
            return midpoint

Method này cho phép chúng ta tìm các phần tử trong một list mà không cần phải nhờ đến giải pháp nặng nề của dictionary. Đặc biệt khi một list về bản chất là đã được sắp xếp, việc tìm kiếm nhị phân sẽ hiệu quả hơn rất nhiều (độ phức tạp là O(log n)) so với việc convert dữ liệu sang dictionary rồi thực hiện việc tìm kiếm (tuy việc tìm kiếm với dictionary có độ phức tạp O(1), việc convert cỡ O(n) và ràng buộc không lặp lại key là những điều không mong muốn).

Hơn nữa, module bisect đơn giản hóa rất nhiều quá trình này bằng cách cung cấp các method để dễ dàng thêm các phần tử vào một list trong khi vẫn duy trì việc sắp xếp, cùng với việc tìm kiếm các phần tử sử dụng phương pháp tìm kiếm nhị phân tối ưu hóa (heavily optimized binary search). Nó thực hiện việc này bằng cách cung cấp các hàm thay thế mà ở đó các phần tử được thêm vào sẽ được sắp xếp luôn. Với một list luôn luôn được sắp xếp, chúng ta có thể dễ dàng tìm được các phần tử mong muốn (ví dụ sử dụng module bisect ở đây). Ngoài ra, chúng ta có thể sử dụng bisect để tìm phần tử gần nhất với những giá trị chúng ta tìm kiếm rất nhanh (Ví dụ 3-4). Điều này cực kỳ hữu ích cho việc so sánh hai tập dữ liệu (dataset) tương tự nhau nhưng không không đồng nhất.

Ví dụ 3-4: Tìm các giá trị lân cận với bisect

import bisect
import random

def find_closest(haystack, needle):
    # bisect.bisect_left sẽ trả về giá trị đầu tiên trong haystack lớn hơn so với needle
    i = bisect.bisect_left(haystack, needle)
    if i == len(haystack):
        return i - 1
    elif haystack[i] == needle:
        return i
    elif i > 0:
        j = i - 1
        if haystack[i] - needle > needle - haystack[j]:
            return j
    return i

important_numbers = []
for i in xrange(10):
    new_number = random.randint(0, 1000)
    bisect.insort(important_numbers, new_number)

# important_numbers sẽ được sắp xếp theo thứ tự bởi vì chúng ta insert các phần tử mới với bisect.insort
print important_numbers
closest_index = find_closest(important_numbers, -250)
print "Giá trị gần nhất với -250: ", important_numbers[closest_index]
closest_index = find_closest(important_numbers, 500)
print "Giá trị gần nhất với 500: ", important_numbers[closest_index]
closest_index = find_closest(important_numbers, 1100)
print "Giá trị gần nhất với 1100: ", important_numbers[closest_index]

Nói chung, điều này dính líu đến một rule cơ bản trong việc viết code hiệu quả: chọn đúng cấu trúc dữ liệu. Mặc dù có thể có nhiều cấu trúc dữ liệu hiệu quả hơn cho các thao tác cụ thể, cái giá của việc convert dữ liệu sang các cấu trúc dữ liệu đó sẽ làm cho chúng ta nản lòng.

Phần I của loạt bài dịch về High Performance Python - Lists and Tuples xin được dừng lại ở đây