Giới thiệu

Làm việc với các biến trong phân tích dữ liệu luôn đặt ra câu hỏi: Các biến phụ thuộc, liên kết và thay đổi với nhau như thế nào? Các biện pháp hiệp phương sai và hệ số tương quan tuyến tính giúp thiết lập điều này.

Hiệp phương sai mang lại sự thay đổi giữa các biến. Chúng ta sử dụng hiệp phương sai để đo lường mức độ hai biến thay đổi với nhau. Hệ số tương quan tuyến tính tiết lộ mối quan hệ giữa các biến. Chúng ta sử dụng mối tương quan để xác định mức độ liên kết chặt chẽ của hai biến với nhau.

Phương sai và Tương quan - Nói một cách đơn giản

Cả hiệp phương sai và tương quan là hai khái niệm trong lĩnh vực xác suất thống kê, đều nói về mối quan hệ giữa các biến. Hiệp phương sai xác định mối liên kết có hướng giữa các biến. Giá trị hiệp phương sai nằm trong khoảng từ−∞ đến +∞ trong đó giá trị dương biểu thị rằng cả hai biến chuyển động theo cùng một hướng và giá trị âm biểu thị rằng cả hai biến chuyển động ngược chiều nhau.

Tương quan là một thước đo thống kê được tiêu chuẩn hóa thể hiện mức độ mà hai biến có liên quan tuyến tính với nhau (nghĩa là chúng thay đổi cùng nhau với tốc độ không đổi bao nhiêu). Độ mạnh và sự kết hợp định hướng của mối quan hệ giữa hai biến được xác định theo mối tương quan và nó nằm trong khoảng từ -1 đến +1. Tương tự như hiệp phương sai, giá trị dương biểu thị rằng cả hai biến chuyển động theo cùng một hướng trong khi giá trị âm cho chúng ta biết rằng chúng di chuyển theo các hướng ngược nhau.

Cả hiệp phương sai và tương quan đều là những công cụ quan trọng được sử dụng trong việc thăm dò dữ liệu để lựa chọn đối tượng địa lý và phân tích đa biến. Ví dụ, một nhà đầu tư đang tìm cách phân tán rủi ro của danh mục đầu tư có thể tìm kiếm các cổ phiếu có hiệp phương sai cao, vì điều đó cho thấy giá của chúng tăng cùng một lúc. Tuy nhiên, chỉ riêng một chuyển động tương tự là chưa đủ. Sau đó, nhà đầu tư sẽ sử dụng số liệu tương quan để xác định mức độ liên kết chặt chẽ giữa các giá cổ phiếu đó với nhau.

Thiết lập cho code Python - Truy xuất dữ liệu mẫu

Hãy xem tập dữ liệu, trên đó chúng tôi sẽ thực hiện phân tích: chúng ta chọn hai cột để phân tích - sepal_length và sepal_width. Trong một tệp Python mới (có thể đặt tên nó là covariance_correlation.py), hãy bắt đầu bằng cách tạo hai danh sách với các giá trị cho thuộc tính sepal_length và sepal_width của flower:

with open('iris_setosa.csv','r') as f:
    g=f.readlines()
    # Each line is split based on commas, and the list of floats are formed 
    sep_length = [float(x.split(',')[0]) for x in g[1:]]
    sep_width  = [float(x.split(',')[1]) for x in g[1:]]

Trong khoa học dữ liệu, nó luôn giúp trực quan hóa dữ liệu bạn đang làm việc. Đây là biểu đồ hồi quy Seaborn (Biểu đồ phân tán + phù hợp hồi quy tuyến tính) của các thuộc tính setosa này trên các trục khác nhau: Về mặt trực quan, các điểm dữ liệu dường như có mối tương quan cao gần với đường hồi quy. Hãy xem liệu các quan sát của chúng ta có khớp với các giá trị hiệp phương sai và tương quan của chúng hay không.

Tính toán hiệp phương sai trong Python

Công thức sau đây tính hiệp phương sai: Trong công thức trên,

• xi, yi - are individual elements of the x and y series
• x̄, y̅ - are the mathematical means of the x and y series
• N - is the number of elements in the series

Mẫu số là N đối với toàn bộ tập dữ liệu và N - 1 đối với mẫu. Vì tập dữ liệu của chúng ta là một mẫu nhỏ của toàn bộ tập dữ liệu Iris nên chúng ta sử dụng N - 1.

def covariance(x, y):
    # Finding the mean of the series x and y
    mean_x = sum(x)/float(len(x))
    mean_y = sum(y)/float(len(y))
    # Subtracting mean from the individual elements
    sub_x = [i - mean_x for i in x]
    sub_y = [i - mean_y for i in y]
    numerator = sum([sub_x[i]*sub_y[i] for i in range(len(sub_x))])
    denominator = len(x)-1
    cov = numerator/denominator
    return cov

with open('iris_setosa.csv', 'r') as f:
    ...
    cov_func = covariance(sep_length, sep_width)
    print("Covariance from the custom function:", cov_func)

Đầu tiên chúng ta tìm các giá trị trung bình của bộ dữ liệu. Sau đó, chúng ta sử dụng khả năng hiểu danh sách để lặp lại mọi phần tử trong hai chuỗi dữ liệu của chúng ta và trừ giá trị của chúng cho giá trị trung bình.

Sau đó, chúng ta sử dụng các giá trị trung gian đó của hai chuỗi 'và nhân chúng với nhau trong một cách hiểu danh sách khác. Chúng ta tính tổng kết quả của danh sách đó và lưu trữ nó dưới dạng tử số. Mẫu số dễ dàng hơn rất nhiều để tính toán, hãy nhớ tách nó đi 1 khi bạn đang tìm hiệp phương sai cho dữ liệu mẫu!

Sau đó, chúng ta trả về giá trị khi tử số được chia cho mẫu số của nó, điều này dẫn đến hiệp phương sai. Ta được kết quả

Covariance from the custom function: 0.09921632653061219

Giá trị dương biểu thị rằng cả hai biến chuyển động theo cùng một hướng.

Tính toán hệ số tương quan trong Python

Để thể hiện mối quan hệ giữa 2 biến là “mạnh” hay “yếu”, chúng ta sử dụng correlation thay cho covariance.

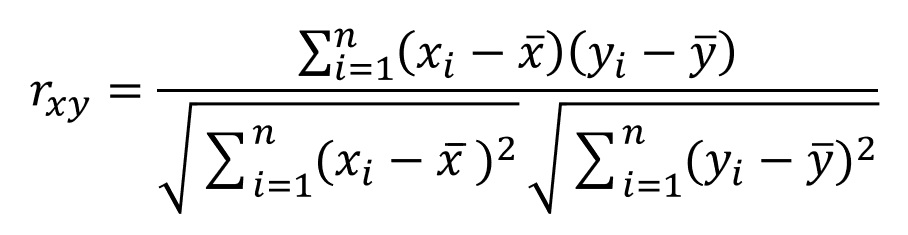
• xi, yi - are individual elements of the x and y series
• The numerator corresponds to the covariance
• The denominators correspond to the individual standard deviations of x and y

def correlation(x, y):
    # Finding the mean of the series x and y
    mean_x = sum(x)/float(len(x))
    mean_y = sum(y)/float(len(y))
    # Subtracting mean from the individual elements
    sub_x = [i-mean_x for i in x]
    sub_y = [i-mean_y for i in y]
    # covariance for x and y
    numerator = sum([sub_x[i]*sub_y[i] for i in range(len(sub_x))])
    # Standard Deviation of x and y
    std_deviation_x = sum([sub_x[i]**2.0 for i in range(len(sub_x))])
    std_deviation_y = sum([sub_y[i]**2.0 for i in range(len(sub_y))])
    # squaring by 0.5 to find the square root
    denominator = (std_deviation_x*std_deviation_y)**0.5 # short but equivalent to (std_deviation_x**0.5) * (std_deviation_y**0.5)
    cor = numerator/denominator
    return cor

with open('iris_setosa.csv', 'r') as f:
    ...
    cor_func = correlation(sep_length, sep_width)
    print("Correlation from the custom function:", cor_func)

Vì giá trị này cần hiệp phương sai của hai biến nên hàm khá nhiều lần tính ra giá trị đó. Khi hiệp phương sai được tính, chúng ta tính độ lệch chuẩn cho mỗi biến. Từ đó, mối tương quan chỉ đơn giản là chia hiệp phương sai với phép nhân các bình phương của độ lệch chuẩn. Chạy mã này, chúng ta nhận được kết quả sau, xác nhận rằng các thuộc tính này có mối quan hệ dương (dấu của giá trị, hoặc +, - hoặc none nếu 0) và mạnh (giá trị gần bằng 1):

Correlation from the custom function: 0.7425466856651597

Nguồn: https://stackabuse.com/covariance-and-correlation-in-python/