Giới Thiệu Về Các Hệ Mã Hóa

Trong thời đại số hóa ngày nay, mật mã đóng một vai trò rất quan trọng. Và tôi nghĩ người lập trình viên cần phải trang bị các kiến thức cơ bản về mã hóa. Vì vậy, trong bài viết này tôi muốn giới thiệu đến các bạn tổng quan về các hệ mật mã, cách chúng làm việc, ưu và nhược điểm của từng hệ mật mã, cách chúng phối hợp, bổ sung cho nhau như thế nào.

Vậy mật mã quan trọng như thế nào, và những ứng dụng của nó trong đời sống cũng như kỹ thuật là gì?

Vai trò của mã hóa

Mã hóa giúp chúng ta che dấu thông tin, đảm bảo tính riêng tư, bí mật của các thông tin nhạy cảm.

Có thể nói mật mã được ứng dụng trong mọi ngóc ngách của công nghệ: lúc bạn lướt facebook, tìm kiếm trên google (riêng cá nhân tôi vẫn thích dùng duckduckgo.com hơn), check mail, giao dịch ngân hàng hay lúc tôi đang gõ những dòng blog này, v.v...

Hơn nữa mật mã còn được sử dụng trong bầu cử, đấu giá ẩn danh, hay mới nổi lên gần đây đó là sự xuất hiện của đồng tiền ảo bitcoin.

Trước khi đi vào tìm hiểu các hệ mã hóa khác nhau, tôi nghĩ cần phải hiểu thế nào là một hệ mã hóa.

Định nghĩa hệ mã hóa

Một hệ mã hóa gồm hai thuật toán, ta ký hiệu E (Encryption - hàm mã hóa) và D (Decryption - hàm giải mã), và có một điểm cần lưu ý đó là (E, D) phải có thời gian tính đa thức. Ta ký hiệu M là tập các bản rõ (plain text), K là tập các khóa và C là tập các bản mã, hàm (E, D) phải thỏa mãn điều kiện sau:

Với m thuộc M, k thuộc K: E(m, k) = c (thuộc C)
=> D(c, k) = D(E(m, k), k) = m

Thông thường hàm mã hóa E là đa định, tức là với đầu vào (m, k) cố định, sẽ cho ra các đầu ra c khác nhau. Và hàm giải mã D là đơn định, từ đầu vào (c, k) sẽ cho ra một bản rõ duy nhất. Đây cũng là điều hiển nhiên, một hàm giải mã không thể cho ra nhiều đầu ra khác nhau.

Có hai hướng để phân loại các hệ mật mã:

• Nếu xét về số bit xử lý, ta có hệ mã hóa dòng và mã hóa khối
• Nếu xét theo loại khóa, ta có hệ mã đối xứng (hay còn gọi là khóa bí mật - Private Key) và hệ mã hóa bất đối xứng (hay còn gọi là khóa công khai - Public Key)

Hệ mã dòng - Stream Cipher

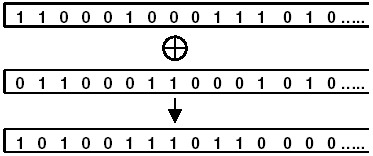
Với các hệ mã dòng (stream cipher), ta sẽ xử lý trên từng bit của bản rõ. Một hệ mã dòng rất nổi tiếng đó là One Time Pad (OTP), lưu ý các bạn đừng nhầm lẫn với One Time Password. Với bản rõ m và khóa k có cùng độ dài theo bit, One-Time-Pad được xác định như sau:

E(m, k) = m XOR k = c
D(c, k) = c XOR k = (m XOR k) XOR k = m

Với OTP, khóa k phải đáp ứng 3 điều kiện sau đây:

• Độ dài của khóa phải bằng kích thước bản rõ.
• Khóa phải được chọn hoàn toàn ngẫu nhiên (truly random)
• Và khóa chỉ được sử dụng một lần

Nếu thỏa mãn 3 điều kiện trên, hệ mã OTP sẽ là an toàn tuyệt đối (perfect security) theo định lý của Clause Shannon, tức là kẻ tấn công sẽ không thể biết được thông tin gì của bản rõ m chỉ từ bản mã c.

Bởi vì các hàm mã-hóa/giải-mã chỉ đơn giản là thực hiện phép toán XOR trên các bit của dữ liệu đầu vào, do đó OTP cho ta tốc độ tính toán rất nhanh.

Do khóa có độ dài bằng bản rõ, nên nếu ta có thể truyền khóa một cách bí mật đến bên nhận thì ta cũng có thể sử dụng cách đó để truyền luôn bản rõ. Đây cũng nhược điểm của OTP. Trong thực tế, người ta thường chọn ngẫu nhiên một khóa k có độ dài nhỏ hơn rất nhiều so với bản rõ, và dùng một hàm tạo số ngẫu nhiên (Pseudo Random Generator - PRG) để mở rộng độ dài của khóa k đó.

Vì vậy, biến thể của OTP được dùng trong thực tế như sau:

E'(m, k) = E(m, PRG(k)) = m XOR PRG(k) = c
D'(c, k) = D(c, PRG(k)) = (m XOR PRG(k)) XOR PRG(k) = m
trong đó, k có kích thước nhỏ hơn rất nhiều so với m.

Hệ mã khối - Block Cipher

Các hệ mã khối, giống như tên gọi, thực hiện tính toán trên từng khối bit có kích thước cố định, thông thường là 64 hoặc 128 bit. Vì vậy khi đầu vào bản rõ có độ dài không là bội số của khối, ta cần phải thực hiện thao tác đệm (padding) sao cho số bit của đầu vào phải là bội số của khối.

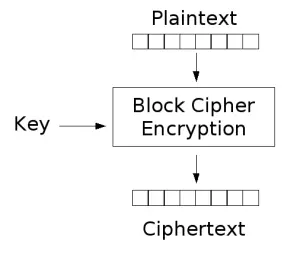nguồn: http://imps.mcmaster.ca/courses/SE-4C03-07/

Các hệ mã khối nổi tiếng đó là DES có kích thước khối là 64 (tức là mỗi lần mã hóa một khối bản rõ 64 bits và cho ra khối bản mã 64 bít) và kích thước khóa là 56 bits; AES có kích thước khối là 128 bit, và kích thước khóa là 128, 192 hoặc 256bit.

Thông thường block cipher chậm hơn so với stream cipher, nhưng làm việc tốt với những khối dữ liệu đã biết trước kích thước, ví dụ mã hóa file, mã hóa tin nhắn trên các giao thức như là HTTP ...

Hệ mã đối xứng - Private Key

Các hệ mã đối xứng sử dụng chung một khóa K cho cả hai hàm mã hóa và giải mã.

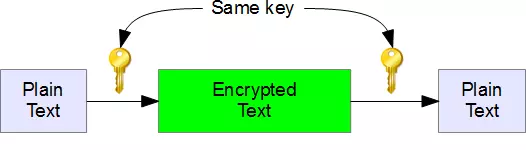
Các ví dụ về hệ mã dòng (OTP) và mã khối (DES, AES) đều là các hệ mã đối xứng.

Có tốc độ tính toán nhanh, Nhưng lại khó để vận chuyển khóa

Hệ mã bất đối xứng - Public Key

Vấn đề đối với các hệ mã đối xứng đó là rất khó để trao chuyển khóa một cách bí mật và các khóa thường gắn liền với một phiên làm việc. Do đó rất khó để quản lý khóa, hơn nữa hệ mã đối xứng không cung cấp cho chúng ta cơ chế chữ ký điện tử.

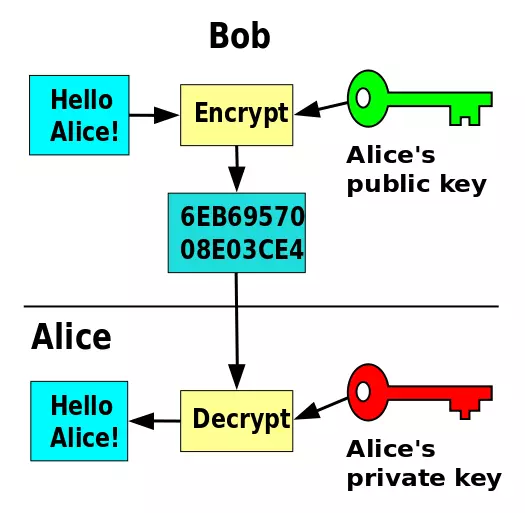nguồn: https://en.wikipedia.org

Vì vậy, các hệ mã khóa công khai đã ra đời để giải quyết các vấn đề trên, ý tưởng của hệ mã khóa công khai đó là mỗi khóa sẽ gắn liền với một người sử dung (thay vì gắn liền với một phiên làm việc giữa 2 người dùng). Trong hệ mã khóa công khai, khóa sẽ bao gồm một bộ gồm 2 khóa PK (Public Key) và SK (Secret Key). Tin nhắn mã hóa với khóa PK sẽ được giải mã với khóa SK và ngược lại. Khóa PK sẽ được công khai, vì vậy ai cũng có thể sử dụng khóa đấy để mã hóa rồi gửi tin nhắn bí mật cho A, nhưng chỉ có A mới có thể giải mã tin nhắn đó (do chỉ có A mới có khóa SK).

Sơ đồ chung của hệ mã như sau:

E(m, pk) = c
D(c, sk) = m

Một hệ mã hóa công khai rất nổi tiếng đó là RSA

So với các hệ mã hóa đối xứng, thì hệ mã hóa bất đối xứng có tốc độ tính toán chậm hơn rất nhiều. Vì vậy, người ta thường dùng hệ mã bất đối xứng để vận chuyển khóa bí mật, sau đó phiên làm việc sẽ được mã hóa trên khóa chung này (sử dụng các hệ mã đối xứng).

Lời kết

Tôi hy vọng bài viết cung cấp cho các bạn những thông tin hữu ích và tổng quan về các hệ mật mã - một ngành khoa học cực kỳ lý thú.

Rất mong nhận được góp ý từ tất cả mọi người. Thank you!