Giới thiệu về B-tree index trong database

Khi nói đến tăng hiệu năng của database, việc đầu tiên mà chúng ta nghĩ đến sẽ là đánh index cho các trường trong một bảng dữ liệu. Trước nay chúng ta đã quá quen với khái niệm này tuy nhiên hiểu được nó là gì và cụ thể như thế nào thì đa số chúng ta còn rất mơ hồ, bài viết hôm nay mạo phép đi cắt ghép từ nhiều nguồn nhằm giải thích rõ hơn cơ chế hoạt động cũng như tác dụng thực sự của index trong database.

Tại sao lại cần đánh index trong database

Giả sử bạn cần lưu trữ một danh sách các member theo tên, và lấy ra một cái tên khi cần thiết. việc đơn giản nhất mà chúng ta có thể làm là lưu vào một array và thêm giá trị vào array đó khi có một item mới. Tuy nhiên để kiểm tra xem một item đã tồn tại trong mảng hay chưa thì bạn cần duyệt mảng , hên xui thì có thể tìm đúng được trong lần đầu tiên, đen thì bạn phải tìm đến khi duyệt đến hết mảng.

Để tiết kiệm thời gian tìm kiếm, chúng ta sử dụng một số thuật toán, trong đó có thể nói đến binary seach, Mỗi khi muốn search một phần tử trong mảng đã được sắp xếp, chúng ta chọn ra một value nằm giữa mảng và so sánh, nếu phần tử muốn search mà lớn hơn phần tử giữa ấy thì ta chọn phần bên phải, ngược lại thì chọn phần bên trái, cứ thế chia đôi cho đến khi tìm được chỗ của phần tử cần tìm.

Ví dụ trên là một dạng của Binary-Tree, tuy nhiên thay vì lưu trữ value của mảng thì nó giữ con trỏ , trỏ tới node tiếp theo.

B-Tree là gì?

B-tree là một kiến trúc dữ liệu, để lưu trữ dữ liệu dưới dạng các node được sắp xếp theo thứ tự nhất định.

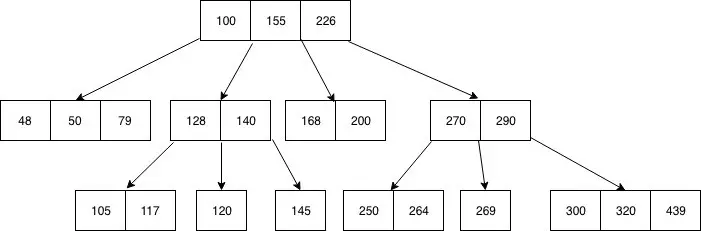
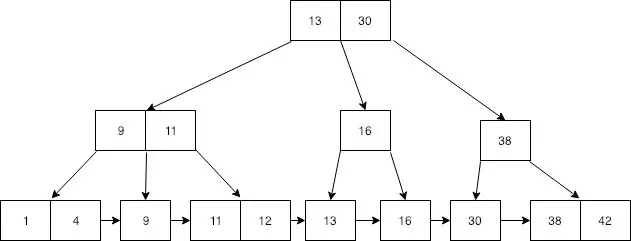
B-Tree lưu trữ dữ liệu theo kiểu mỗi node lưu trữ key theo thứ tự tăng dần, mỗi node này lại chứa 2 liên kết đến những node trước và sau nó. Node bên trái có key <= key node hiện tại, còn node bên phải thì có key >= key của node hiện tại. Nếu một node mà có n keys thì nó sẽ có tối đa là n + 1 node con.

B-Tree index tăng tốc độ truy vấn dữ liệu vì storage engine không phải duyệt cả bảng để tìm kiếm dữ liệu mà nó sẽ đi từ node root. các vị trí root node sẽ chưa con trỏ tới những node con, nó tìm đúng con trỏ bằng cách nhìn vào các giá trị trong node con và bằng việc xác định các giới hạn trên và dưới của một node, giúp storage engine dễ dàng tìm kiếm sự tồn tại hay không của một giá trị.

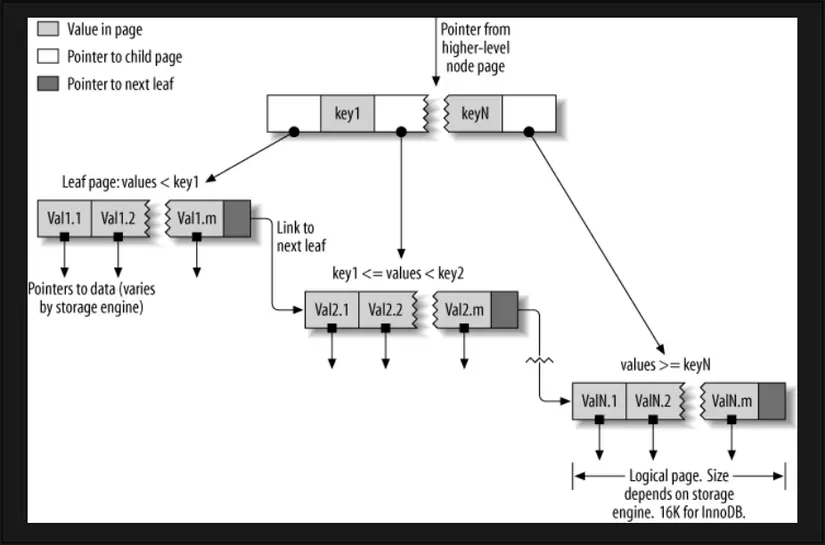
Cùng xem cấu trúc tổng quát của B-Tree

Cách B-Tree Index hoạt động trong database

Về cấu trúc của B-Tree khá phức tạp vì nó không chỉ lưu trữ index mà còn lưu trữ cả value liên kết với index ấy, giá trị này liên kết đến record dữ liệu thực tế trong database, cặp đôi key-value này được gọi là payload.

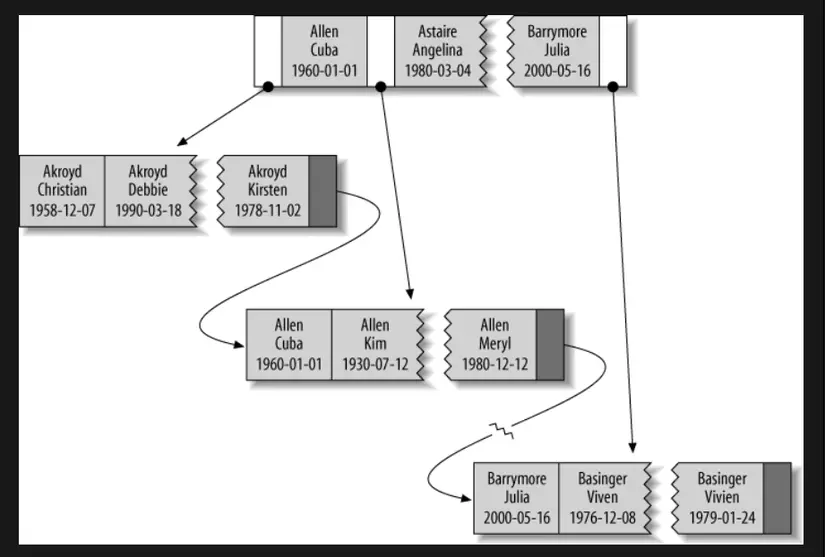
Chúng ta cùng xem một ví dụ để hiểu rõ hơn về cơ chế này lưu trữ và tìm kiếm kiểu B-Tree này

Đầu tiên là tạo một bảng dữ liệu

CREATE TABLE People (
last_name varchar(50) not null,
first_name varchar(50) not null,
dob date not null,
gender enum('m', 'f')not null,
key(last_name, first_name, dob)
);

Index ở đây chính là last_name, first_name, dob trong bảng People.

Chú ý rằng trình tự của index sẽ phụ thuộc vào thứ tự column trong quá trình chúng ta tạo bảng, khi một giá trị trùng nhau thì giá trị tiếp theo sẽ được lấy làm tiêu chí để sắp xếp, ví dụ 2 người có cùng tên là Basinger Viven nhưng họ khác ngày sinh nên ngày sinh sẽ được dùng để sắp xếp.

Những kiểu truy vấn có thể dùng với B-Tree

B-Tree rất hữu ích trong việc tìm kiểu full value, hoặc trong một dải value (key range), hoặc một tiền tố xác định (key prefix). Như trong ví dụ trên chúng ta có thể thấy, B-tree

Tìm kiếm đầy đủ giá trị (Full value)

Là việc tìm kiếm tất cả đầy đủ giá trị trong những column đã được đánh index ví dụ chúng ta có thể tìm kiếm những người có tên Cuba Allen và sinh năm 1960-01-01

Tìm kiếm tiền tố bên trái

Chúng ta có thể tìm kiếm tất cả những người có tên Allen, tuy nhiên điều này chỉ ứng dụng với column đầu tiên trong index.

Tìm kiếm tiền tố column

Chúng ta có thể tìm kiếm những người có last_name bắt đầu bằng chữ cái J, và điều này cũng chỉ hữu ích cho column đầu tiên của index.

Tìm kiếm trong một giải các giá trị

Điều này giúp chúng ta tìm kiếm những người có tên nằm trong khoảng từ Allen đến Barymore. Tuy nhiên nó cũng chỉ hữu ích với column đầu tiên của Index.

Tìm kiếm một phần và một dải trong phần tiếp theo

Giups chúng ta tìm kiếm những người có last_name là Allen và có first_name bắt đầu bằng ký tự K. Nó chỉ có tác dụng với last_name và một dải của first_name.

Bởi vì các node trên tree đã được sắp xếp chính vì thế chúng có thể thực hiện cả 2 việc là tìm kiếm giá trị và tìm kiếm trên một tập đã sắp xếp.

Một số giới hạn của B-Tree

• Giới hạn lớn nhất của B-Tree chính là việc nó chỉ tìm kiếm tốt tại cột ngoài cùng bên trái của index.
• Bạn không thể bỏ qua columns trong index ví dụ không thể chỉ tìm kiếm từ last_name và dob mà bỏ qua first_name
• storage engine không thể tối ưu truy vấn với bấy kỳ column nào nằm bên phải một dải giá trị, ví dụ nếu như bạn query WHERE last_name="Smith" AND first_name LIKE 'J%' AND dob='1976-12-23' Thì sẽ chỉ có tác dụng trên 2 cột đầu tiên bên trai trong index. Bởi vì LIKE ở đây được hiểu như một dải các giá trị.

Qua đây chúng ta có thể thấy rằng việc sắp xếp các column trong index là vô cùng quan trọng , Để có hiệu suất tối ưu việc tạo chỉ mục cho cùng một column với các thứ tự khác nhau là cần thiết.

Tạo B-Tree index trong mysql

Tạo Index lúc tạo bảng

CREATE TABLE t(
   c1 INT PRIMARY KEY,
   c2 INT NOT NULL,
   c3 INT NOT NULL,
   c4 VARCHAR(10),
   INDEX (c2,c3) 
);

Insert thêm index vào bảng có sẵn

CREATE INDEX index_name ON table_name (column_list)

Add thêm index cho một column

CREATE INDEX idx_c4 ON t(c4);

Kết luận

Trên đây là một chút giới thiệu về khái niệm đánh chỉ số (indexing) trong database, thông thường khi nghe tới indexing người ta có thể hiểu nó là B-Tree, ngoài B-Tree thì còn một dạng khác gọi là Hash-index, tuy nhiên mình sẽ không nói đến trong bài này. Mục đích là để tăng performance của hệ thống, truy vấn nhanh hơn, tuy rằng nhược điểm lớn là insert hay update sẽ bị chậm đi vì nó cần sắp xếp lại chỉ số , giống như việc sắp xếp sách trên giá vậy, nó có tác dụng cho lần tìm kiếm về sau nhưng lại tốn thời gian để bạn tìm được một nơi đặt phù hợp. Hy vọng bài viết phần nào giúp ích được cho các bạn. Thanks!