Giới thiệu thuật toán Kd Trees (Nearest neighbour search)

Sơ lược:

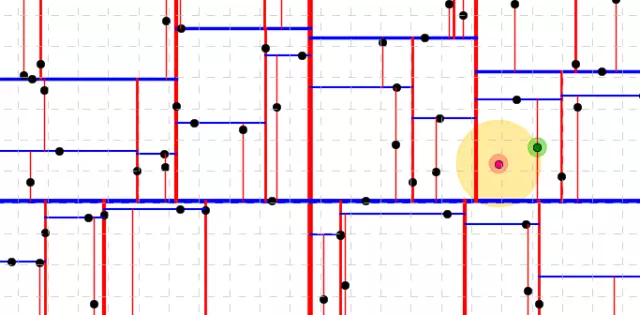
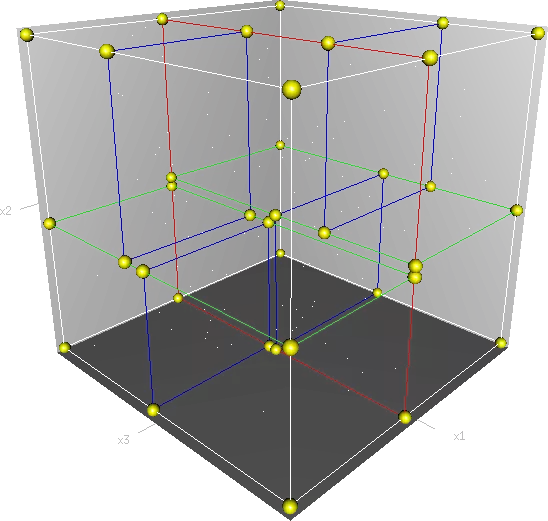
• Kd-trees dùng để tìm kiếm các dữ liệu gần, liên quan nhất (neighbouring data points) trong miền không gian 2 chiều, hoặc nhiều chiều.
• Kd-trees thuộc họ Nearest neighbor (NN) search.

Tóm tắt:

1. Cách build Kd-trees từ tranning data:

• chọn 1 chiều random, tìm toạ độ trung bình, chia data theo toạ độ đó, lặp lại.

2. Cách tìm các dữ liệu liên quan cho point (7,4)

• tìm các phân vùng chứa điểm (7,4)
• so sánh khoảng cách điểm đó tới tất cả các điểm trong phân vùng để chọn cái gần nhất.

Chi tiết:

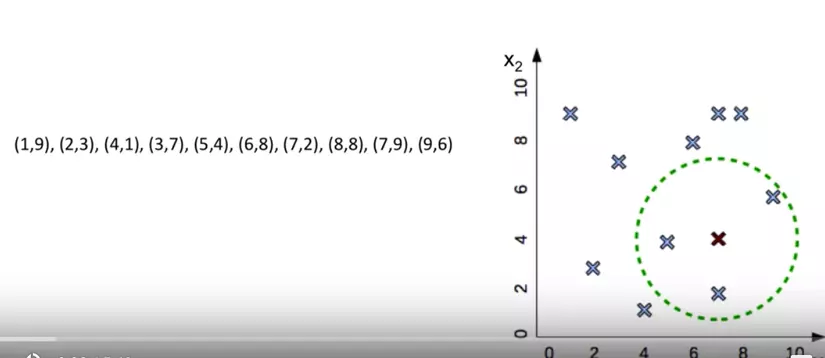
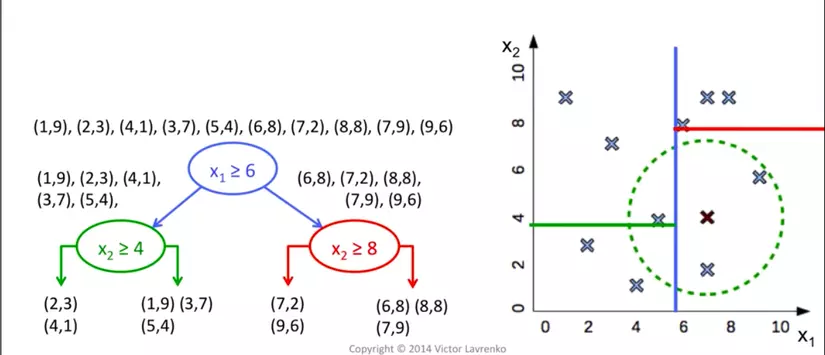
1. Code build tree:

from collections import namedtuple
from operator import itemgetter
from pprint import pformat
 
class Node(namedtuple('Node', 'location left_child right_child')):
 
    def __repr__(self):
        return pformat(tuple(self))
 
def kdtree(point_list, depth=0):
    """ build K-D tree
    :param point_list list of input points
    :param depth      current tree's depth
    :return tree node
    """
 
    # assumes all points have the same dimension
    try:
        k = len(point_list[0])
    except IndexError:
        return None
 
    # Select axis based on depth so that axis cycles through
    # all valid values
    axis = depth % k
 
    # Sort point list and choose median as pivot element
    point_list.sort(key=itemgetter(axis))
    median = len(point_list) // 2         # choose median
 
    # Create node and construct subtrees
    return Node(
        location=point_list[median],
        left_child=kdtree(point_list[:median], depth + 1),
        right_child=kdtree(point_list[median + 1:], depth + 1)
    )

2. Từ tree có được, ta build hàm tìm các điểm neighbour của một điểm cho trước:

Cách search như sau:

• Bắt đầu root node, move qua các nhánh một cách đệ quy.
• Trong khi lướt qua các nhánh, thuật toán sẽ lưu lại node có khoảng cách ngắn nhất với khoảng cách chưa target point (là điểm cần tìm neghibour), được gọi là current best (tốt nhất hiện tại)
• Nếu node hiện tại gần target point hơn current best, nó sẽ trở thành current best.
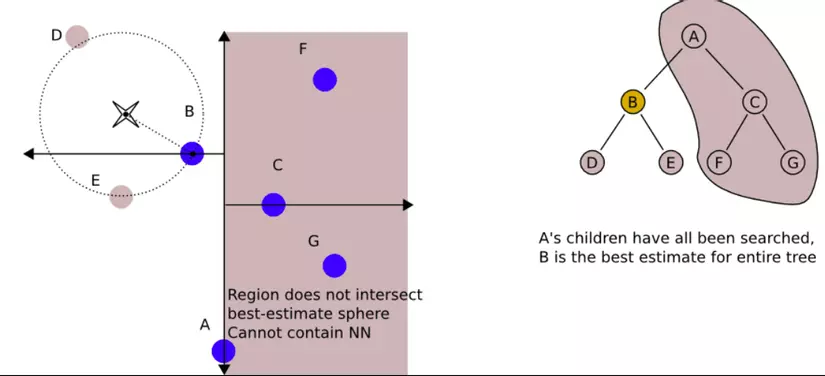
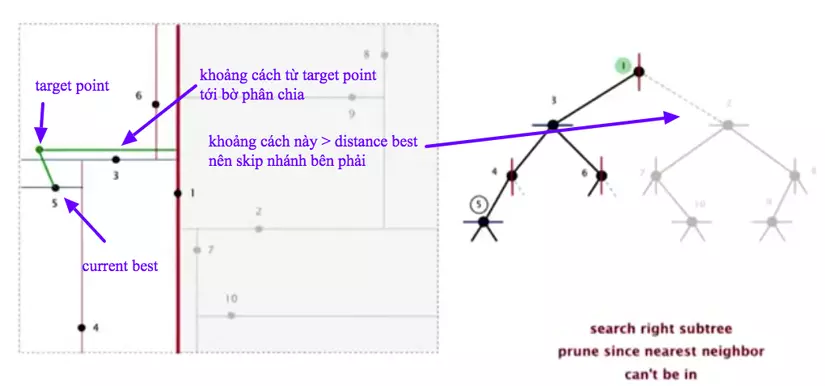
• Trong khi di chuyển nó sẽ check xem, với điểm current best ở nhánh trái thì distance best (khoảng cách từ target point tới current best) có ngắn hơn khoảng cách từ target point tới bờ phân chia hay không, nếu ngắn hơn tức là bên nhánh trái đã cho kết quả tốt nhất và ta không cần tìm tiếp bên phải, nếu dài hơn tức là có lẽ sẽ có 1 điểm nào đó bên phải cho khoảng cách tới target point tốt hơn nên ta phải tiếp tục loop qua các nhánh bên phải.
• Với mỗi nhánh, thuật toán hoàn thành cho tới khi chạm leaf node.

Code

nearest_nn = None           # nearest neighbor (NN)
distance_nn = float('inf')  # distance from NN to target
 
def nearest_neighbor_search(tree, target_point, hr, distance, nearest=None, depth=0):
    """ Find the nearest neighbor for the given point (claims O(log(n)) complexity)
    :param tree         K-D tree
    :param target_point given point for the NN search
    :param hr           splitting hyperplane
    :param distance     minimal distance
    :param nearest      nearest point
    :param depth        tree's depth
    """
 
    global nearest_nn
    global distance_nn
 
    if tree is None:
        return
 
    k = len(target_point)
 
    cur_node = tree.location         # current tree's node
    left_branch = tree.left_child    # its left branch
    right_branch = tree.right_child  # its right branch
 
    nearer_kd = further_kd = None
    nearer_hr = further_hr = None
    left_hr = right_hr = None
 
    # Select axis based on depth so that axis cycles through all valid values
    axis = depth % k
 
    # split the hyperplane depending on the axis
    if axis == 0:
        left_hr = [hr[0], (cur_node[0], hr[1][1])]
        right_hr = [(cur_node[0],hr[0][1]), hr[1]]
 
    if axis == 1:
        left_hr = [(hr[0][0], cur_node[1]), hr[1]]
        right_hr = [hr[0], (hr[1][0], cur_node[1])]
 
    # check which hyperplane the target point belongs to
    if target_point[axis] <= cur_node[axis]:
        nearer_kd = left_branch
        further_kd = right_branch
        nearer_hr = left_hr
        further_hr = right_hr
 
    if target_point[axis] > cur_node[axis]:
        nearer_kd = right_branch
        further_kd = left_branch
        nearer_hr = right_hr
        further_hr = left_hr
 
    # check whether the current node is closer
    dist = (cur_node[0] - target_point[0])**2 + (cur_node[1] - target_point[1])**2
 
    if dist < distance:
        nearest = cur_node
        distance = dist
 
    # go deeper in the tree
    nearest_neighbor_search(nearer_kd, target_point, nearer_hr, distance, nearest, depth+1)
 
    # once we reached the leaf node we check whether there are closer points
    # inside the hypersphere
    if distance < distance_nn:
        nearest_nn = nearest
        distance_nn = distance
 
    # a nearer point (px,py) could only be in further_kd (further_hr) -> explore it
    px = compute_closest_coordinate(target_point[0], further_hr[0][0], further_hr[1][0])
    py = compute_closest_coordinate(target_point[1], further_hr[1][1], further_hr[0][1])
 
    # check whether it is closer than the current nearest neighbor => whether a hypersphere crosses the hyperplane
    dist = (px - target_point[0])**2 + (py - target_point[1])**2
 
    # explore the further kd-tree / hyperplane if necessary
    if dist < distance_nn:
        nearest_neighbor_search(further_kd, target_point, further_hr, distance, nearest, depth+1)

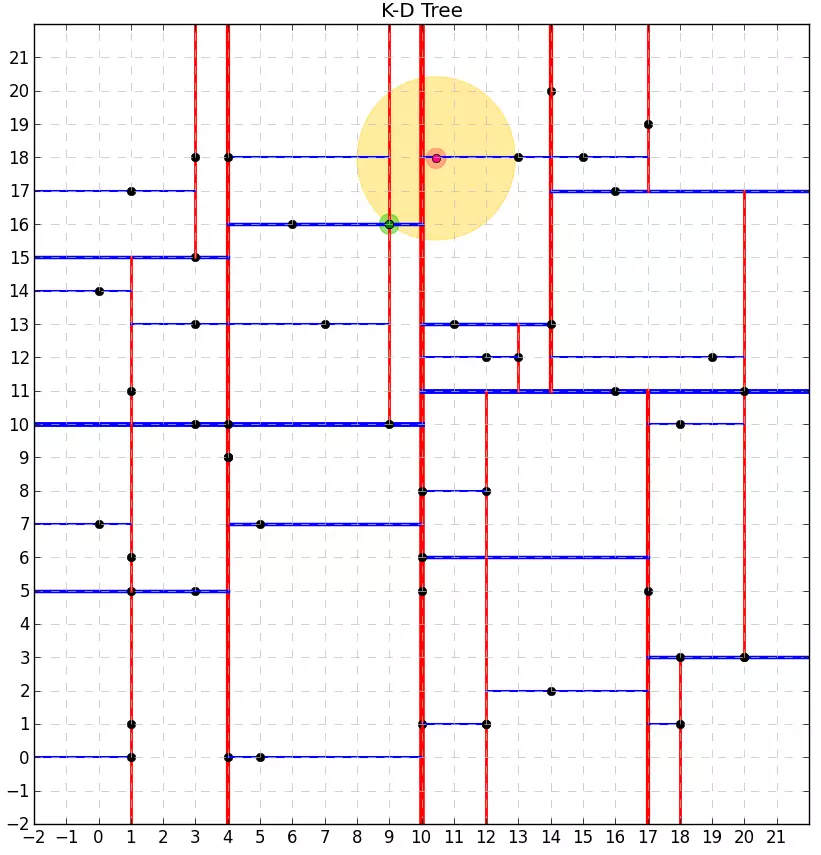
3. Chạy thử:

Dùng với scikit-learn:

1. Dùng sklearn:

>>> import numpy as np
>>> np.random.seed(0)
>>> X = np.random.random((10, 3))  # 10 points in 3 dimensions
>>> tree = KDTree(X, leaf_size=2)              
>>> dist, ind = tree.query([X[0]], k=3)                
>>> print(ind)  # indices of 3 closest neighbors
[0 3 1]
>>> print(dist)  # distances to 3 closest neighbors
[ 0.          0.19662693  0.29473397]

Cảm ơn các bạn đã đọc, happy learning

Reference:

• https://salzis.wordpress.com/2014/06/28/kd-tree-and-nearest-neighbor-nn-search-2d-case/
• http://scikit-learn.org/stable/modules/neighbors.html#kd-tree
• https://en.wikipedia.org/wiki/K-d_tree