Đã đăng vào thg 7 21, 12:44 CH 15 phút đọc

226

Fourier Transform là gì? Vẽ tranh với Discrete Fourier Transform

Nếu bạn chưa từng nghe về Biến Đổi Fourier (Fourier Transform) hay Biến Đổi Fourier Rời Rạc (Discrete Fourier Transform - DFT), đừng lo! Trong bài viết này, chúng ta sẽ cùng khám phá hai khái niệm này một cách đơn giản, dễ hiểu, như thể bạn đang trò chuyện với một người bạn. Hãy tưởng tượng tôi đang giải thích điều này cho bạn một cách dễ hiểu, với những ví dụ thực tế và không quá nhiều thuật ngữ phức tạp.

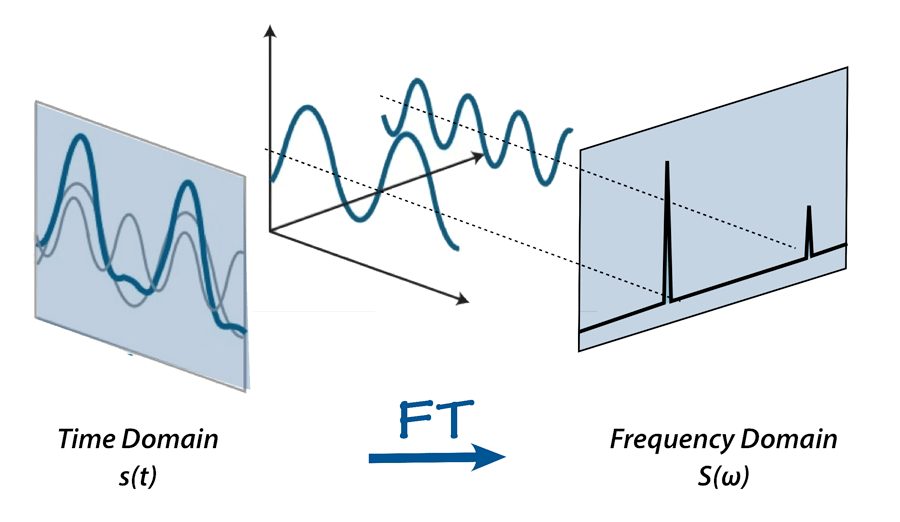
Fourier Transform Visualization

Hình ảnh minh họa: Biến đổi từ miền thời gian sang miền tần số - một tín hiệu phức tạp được phân tách thành các sóng sin đơn giản

1. Biến Đổi Fourier Là Gì?

Hãy bắt đầu với Biến Đổi Fourier. Bạn có thể nghĩ về nó như một công cụ kỳ diệu giúp chúng ta "phân tích" một tín hiệu – bất kỳ thứ gì thay đổi theo thời gian, như âm thanh từ bài hát yêu thích của bạn, sóng biển, hay thậm chí là dữ liệu từ một cảm biến. Ý tưởng chính của Biến Đổi Fourier là: bất kỳ tín hiệu nào cũng có thể được biểu diễn như một tổng của các sóng sin và cosin với các tần số khác nhau.

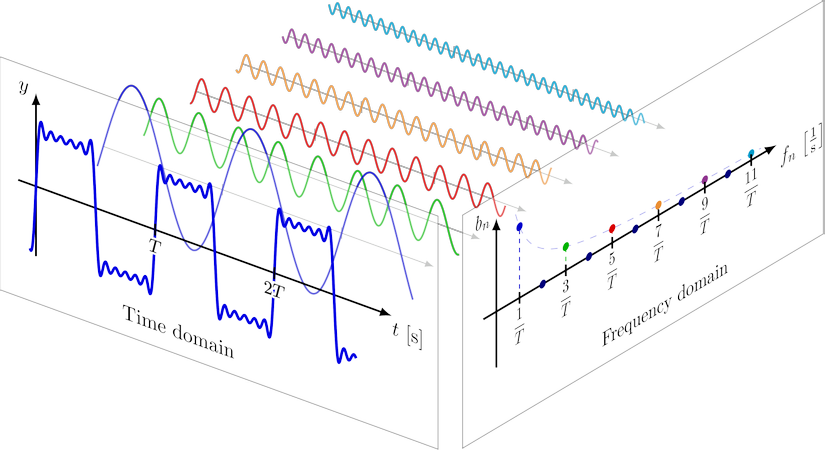
Wave Decomposition

Một sóng phức tạp được phân tách thành các sóng sin thành phần với tần số khác nhau

Tại Sao Điều Này Quan Trọng?

Hãy tưởng tượng bạn đang nghe một bản nhạc. Bản nhạc đó là sự kết hợp của nhiều nốt nhạc khác nhau (tần số cao, thấp, v.v.). Biến Đổi Fourier giống như một "đôi tai siêu phàm" giúp bạn tách từng nốt nhạc đó ra để xem nó đóng góp như thế nào vào bản nhạc tổng thể. Nói cách khác, nó chuyển tín hiệu từ miền thời gian (thay đổi theo thời gian) sang miền tần số (cho bạn thấy các tần số nào đang xuất hiện).

Audio Spectrum Analysis

Ví dụ, nếu bạn có một bài hát, Biến Đổi Fourier có thể cho bạn biết bài hát đó có bao nhiêu âm trầm (tần số thấp), âm trung (tần số trung bình), và âm cao (tần số cao). Điều này rất hữu ích trong xử lý âm thanh, hình ảnh, hay thậm chí là phân tích dữ liệu trong khoa học và kỹ thuật.

Công Thức Biến Đổi Fourier

Đừng sợ công thức! Tôi sẽ giải thích nó một cách đơn giản. Biến Đổi Fourier của một hàm ( f(t) ) (tín hiệu theo thời gian) được định nghĩa như sau:

$X(f) = \int_{-\infty}^{\infty} f(t) e^{-i 2\pi ft} dt$

$f(t)$ : Tín hiệu gốc, ví dụ như cường độ âm thanh tại thời điểm ( t ).
$X(f)$ : Kết quả, cho biết "lượng" của tần số ( f ) trong tín hiệu.
$e^{-i 2\pi ft}$ : Một hàm sóng phức tạp (gồm sin và cosin) giúp chúng ta "quét" qua các tần số khác nhau.

Fourier Transform Formula Visualization

Đừng lo nếu bạn không hiểu hết công thức này. Ý chính là: nó lấy tín hiệu của bạn và chia nhỏ thành các tần số thành phần.

Hình dung trực quan

Hãy nghĩ về một ly sinh tố. Bạn có một hỗn hợp gồm chuối, dâu, và xoài. Biến Đổi Fourier giống như máy xay sinh tố ngược: thay vì trộn các nguyên liệu lại, nó tách chúng ra để bạn biết có bao nhiêu chuối, bao nhiêu dâu, và bao nhiêu xoài trong hỗn hợp. Trong thế giới thực, điều này được dùng để:

Smoothie Analogy

Xử lý âm thanh: Loại bỏ tiếng ồn từ một bản ghi âm.
Xử lý hình ảnh: Nén ảnh JPEG hoặc phát hiện cạnh trong ảnh.
Viễn thông: Tách biệt các tín hiệu trong mạng di động.

2. Biến Đổi Fourier Rời Rạc (DFT) Là Gì?

Bây giờ, chúng ta chuyển sang Biến Đổi Fourier Rời Rạc (Discrete Fourier Transform - DFT). Đây là phiên bản "thực tế hơn" của Biến Đổi Fourier, được dùng khi bạn làm việc với dữ liệu số, như các mẫu âm thanh được ghi lại bởi máy tính hoặc điện thoại.

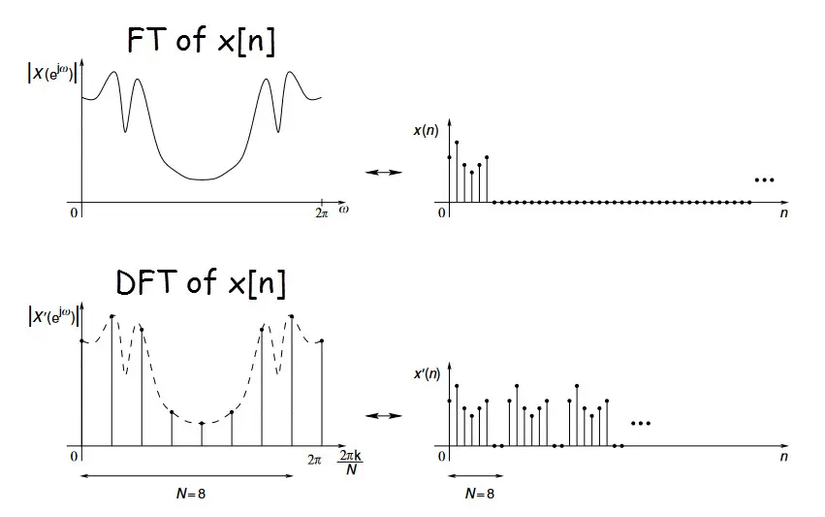Continuous vs Discrete So sánh tín hiệu liên tục vs tín hiệu rời rạc (các điểm sampling)

Tại Sao Cần DFT?

Trong thực tế, máy tính không thể xử lý tín hiệu liên tục (như sóng âm thanh thực sự, kéo dài vô hạn). Thay vào đó, chúng ta lấy mẫu tín hiệu tại các thời điểm cụ thể (ví dụ, 44.100 mẫu mỗi giây cho âm thanh CD). Những mẫu này là rời rạc (discrete), nghĩa là chúng chỉ là một chuỗi số tại các thời điểm nhất định.

DFT lấy chuỗi số này và phân tích nó để tìm ra các tần số thành phần, giống như Biến Đổi Fourier làm với tín hiệu liên tục.

Công Thức DFT

Công thức của DFT trông như thế này:

$X(k) = \sum_{n=0}^{N-1} x(n) e^{-i 2\pi kn / N}$

$x(n)$ : Các mẫu tín hiệu (một chuỗi ( N ) số).
$X(k)$ : Kết quả, cho biết "lượng" của tần số thứ ( k ).
$N$ : Số lượng mẫu.
$e^{-i 2\pi kn / N}$ : Hàm sóng phức tạp, tương tự như trong Biến Đổi Fourier. Nên xem thêm Công thức Euler

DFT Formula Breakdown Phân tích từng thành phần của công thức DFT

Về cơ bản, DFT làm việc với một danh sách số (các mẫu) thay vì một hàm liên tục, và nó tạo ra một danh sách các tần số tương ứng.

Ví Dụ Thực Tế về DFT

Ví dụ một đoạn âm thanh 1 giây với tần số lấy mẫu là 4 Hz (4 mẫu mỗi giây). Bạn sẽ có 4 số: [1, 0, -1, 0]. DFT sẽ phân tích danh sách này và cho bạn biết những tần số nào có trong đoạn âm thanh đó. Từ chuỗi gốc là [1,0,-1,0] ta tìm được các hệ số cho từng sóng là coef=[0,2,0,2], từ các hệ số này ta có thể tái tạo sóng ban đầu, ta có phương trình sau (chỉ là tổng các sóng tại thời điểm $k$ ):

$x[k] =\frac{1}{4} \sum_{i=0}^{3}\texttt{coef}_i e^{-i 2\pi kn / 4}= \frac{1}{2} \left( e^{j \frac{\pi}{2} k} + e^{j \frac{3\pi}{2} k} \right)$

Cụ thể, các phương trình cho từng $n$ :

$x[0] = \frac{1}{2} \left( e^{j \frac{\pi}{2} \cdot 0} + e^{j \frac{3\pi}{2} \cdot 0} \right) = \frac{1}{2} (1 + 1) = 1$
$x[1] = \frac{1}{2} \left( e^{j \frac{\pi}{2}} + e^{j \frac{3\pi}{2}} \right) = \frac{1}{2} (j - j) = 0$
$x[2] = \frac{1}{2} \left( e^{j \pi} + e^{j 3\pi} \right) = \frac{1}{2} (-1 - 1) = -1$
$x[3] = \frac{1}{2} \left( e^{j \frac{3\pi}{2}} + e^{j \frac{9\pi}{2}} \right) = \frac{1}{2} (-j + j) = 0$

Nhận thấy một điều là ta có thể mở rộng sóng này thành miền số thực. Vậy từ các điểm rời rạc ta đã tìm được các hệ số và tái tạo được sóng liên tục ban đầu. Nên DFT được ứng dụng trong rất nhiều tác vụ liên quan đến âm thanh như lưu trữ, thay đổi âm độ.

Ngoài ra: khi bạn dùng ứng dụng như Shazam để nhận diện bài hát, DFT được sử dụng để phân tích các mẫu âm thanh và tìm ra các tần số đặc trưng, từ đó so sánh với cơ sở dữ liệu để tìm bài hát phù hợp.

Fast Fourier Transform (FFT)

Một lưu ý nhỏ: DFT có thể tốn rất nhiều thời gian tính toán nếu bạn có nhiều mẫu dữ liệu. Vì vậy, người ta phát minh ra Fast Fourier Transform (FFT), một thuật toán siêu nhanh để tính DFT. FFT giống như một chiếc xe đua so với việc đi bộ của DFT – nó làm cùng một việc nhưng nhanh hơn rất nhiều!

FFT

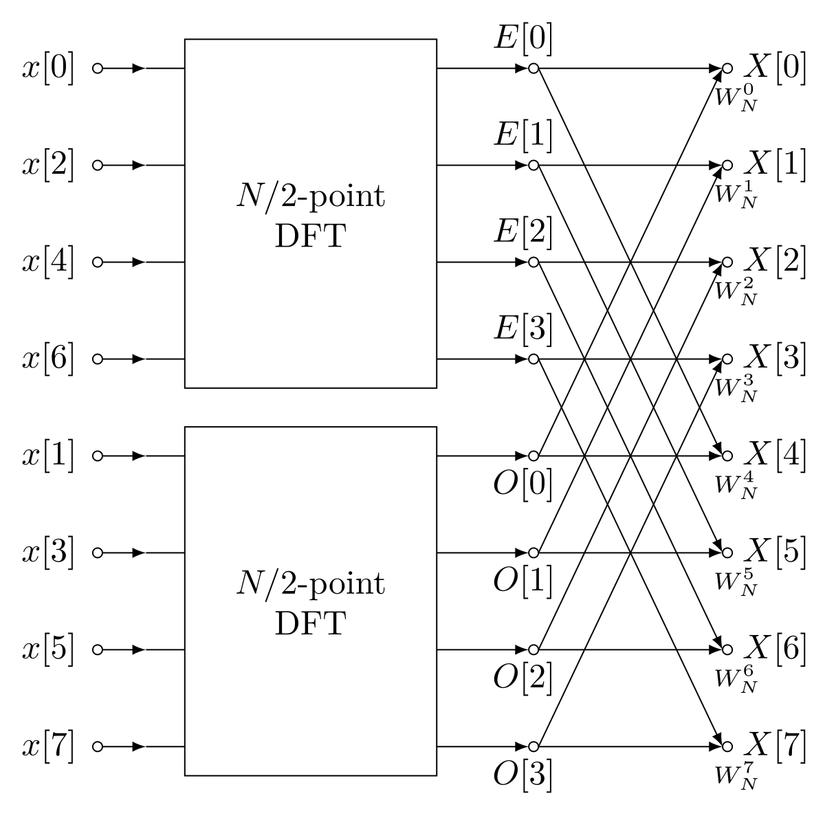
Điều này có thể giảm độ phức tạp từ việc tính từng hệ số, phải xét hết tất cả các điểm, độ phức tạp lên đến $O(n^2)$ . Thành độ phức tạp $O(nlog_2n)$ . Để thấy được vẽ đẹp của FFT, bạn nên xem video của 3b1b tại đây

Các hệ số và các điểm có thể là số phức

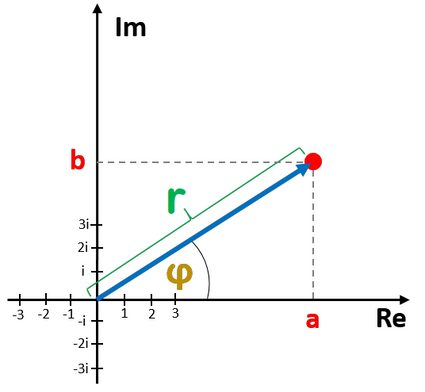
Một điểm thú vị và sâu sắc của DFT là các hệ số $X(k)$ mà nó tạo ra không chỉ là các số thực — chúng là số phức. Điều này có ý nghĩa gì?

Mỗi hệ số phức $X(k)$ có thể được hiểu như một vector quay tròn (rotating vector), hay còn gọi là hàm xoắn (complex exponential). Khi bạn cộng nhiều vector quay với các tốc độ và biên độ khác nhau, bạn có thể tái tạo lại bất kỳ tín hiệu nào. Đây chính là linh hồn của DFT: chuyển tín hiệu thành tổng các chuyển động tròn. Với mỗi hệ số phức có thể suy ra được biên độ và pha ban đầu.

ComplexCoefficient

3. Ứng Dụng Thực Tế

Cả Biến Đổi Fourier và DFT đều có mặt trong cuộc sống hàng ngày:

Âm nhạc: Các ứng dụng như Spotify hoặc Audacity sử dụng DFT để phân tích và xử lý âm thanh.
Hình ảnh: Nén ảnh JPEG hay phát hiện đặc điểm trong hình ảnh y khoa.
Viễn thông: Mã hóa và giải mã tín hiệu trong mạng 4G/5G.
Khoa học: Phân tích sóng địa chấn để dự đoán động đất.

4. Thử vẽ tranh với Fourier Transform

Để làm cho lý thuyết trở nên sinh động hơn, tôi đã tạo ra một dự án thực tế có tên Rustier-DFT-Drawing sử dụng ngôn ngữ lập trình Rust. Dự án này cho phép bạn vẽ hình bằng cách sử dụng DFT để tái tạo các đường cong từ nhiều vòng tròn quay. Quá trình việc xử lý như sau:

Đọc file SVG hoặc cho phép bạn vẽ tự do trên màn hình
Chuyển đổi đường vẽ thành một chuỗi các điểm phức (complex numbers)
Áp dụng DFT để tìm ra các hệ số Fourier
Tái tạo hình vẽ bằng cách sử dụng nhiều vòng tròn quay với các tần số và biên độ khác nhau ints -> DFT coefficients -> rotating circles*

Code

1. Module DFT (src/dft.rs)

Đây là phần code chính, implement thuật toán DFT:

pub fn from_complex_vector(points: &Vec<Complex<f64>>) -> Vec<Complex<f64>> {
    let N: usize = points.len();
    let num_cyc: usize = points.len();
    let mut c = vec![Complex::<f64>::new(0.0,0.0);num_cyc];
    for k in 0..num_cyc {
        for (i, p) in points.iter().enumerate(){
            c[k] += p*Complex::<f64>::new(0.0,-(i as f64)*2.0*PI/(N as f64)*(k as f64)).exp();
        }
        c[k] /= N as f64;
    }
    c
}

Hàm này implement chính xác công thức DFT mà chúng ta đã thảo luận:

Nhận vào một vector các điểm phức (representing tọa độ x,y của đường vẽ)
Tính toán các hệ số Fourier cho mỗi tần số k
Trả về vector các hệ số phức, mỗi hệ số chứa thông tin về biên độ và pha của một vòng tròn

Ở đây, để đơn giản mình chỉ implement thuận toán O(n^2), không phải FFT O(nlogn)

2. Module Interpolation (src/interp.rs)

Phần này xử lý việc chuẩn hóa dữ liệu đầu vào:

pub fn resize_interp(points: &Vec<Complex<f64>>, num_points: usize) -> Vec<Complex<f64>> {
    // Chuyển đổi các điểm thành các đoạn thẳng
    let lines = list_complex_to_lines(points);
    
    // Tính tổng độ dài để phân bố đều các điểm
    let mut sum_len: f64 = 0.0;
    for line in &lines {
        sum_len += line.abs();
    }
    
    // Tạo ra num_points điểm được phân bố đều dọc theo đường vẽ
    // ... (logic interpolation)
}

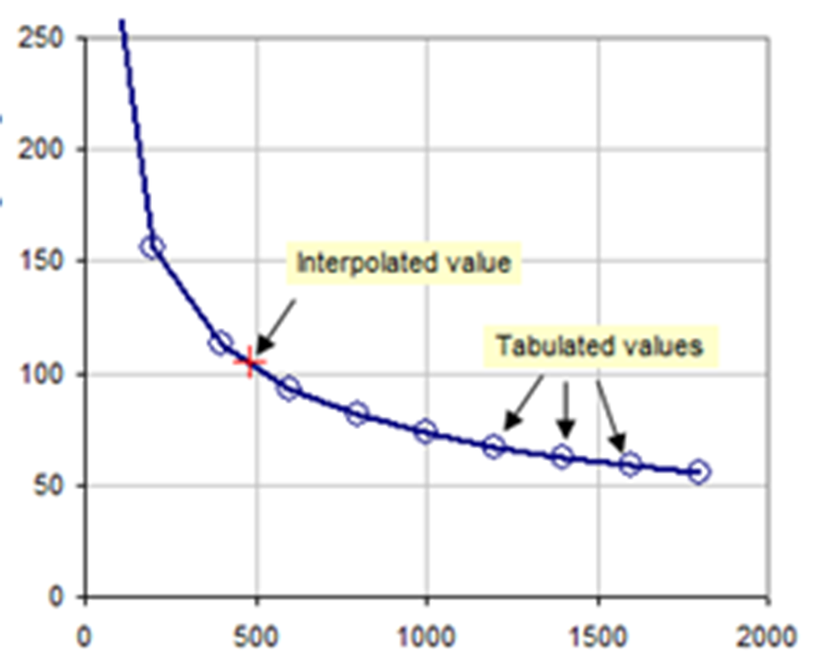
Interpolation Process

Đây là một bước quan trọng vì DFT hoạt động tốt nhất khi các điểm được phân bố đều. Thay vì có các điểm tập trung ở một số vùng và thưa thớt ở vùng khác, module này "resample" lại để có phân bố đều.

3. Module Circles (src/circles.rs)

Ở đây mình sử dụng thư viện Pistol tái tạo hình vẽ từ các vòng tròn, đây là cấu trúc của path được vẽ từ nhiều hình tròn:

pub struct Circles {
    coef: Vec<Complex<f64>>,           // Các hệ số DFT
    current_time: f64,                // Thời gian hiện tại
    screen_offset: Complex<f64>,      // Offset để center hình
    drawed_lines: Vec<interp::Line>,  // Các đường đã vẽ
    enumerate_sorted: Vec<(usize, Complex<f64>)>, // Hệ số được sắp xếp theo độ lớn
}

Module này:

Sắp xếp các hệ số DFT theo độ lớn (amplitude) giảm dần. Để thuận tiện việc làm mượt (smoothing) hình vẽ, nếu cần
Vẽ các vòng tròn từ to đến nhỏ
Mỗi vòng tròn quay với tần số tương ứng với chỉ số k trong DFT
Những điểm cuối cùng tạo ra (trajectory) chính là hình vẽ gốc được tái tạo

4. Module Painting (src/painting.rs)

Cho phép người dùng vẽ tự do:

pub struct Board{
    screen_size: [u32; 2],
    screen_offset: Complex<f64>,
    points: Vec<Complex<f64>>,  // Các điểm người dùng vẽ
}

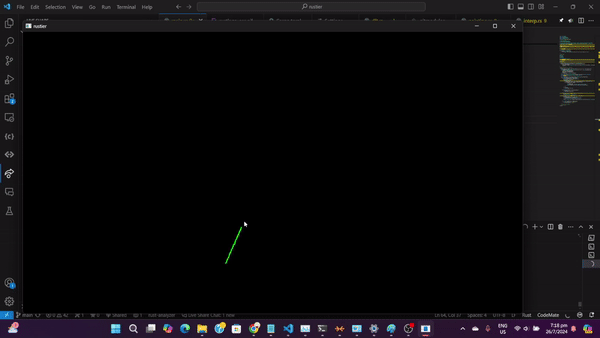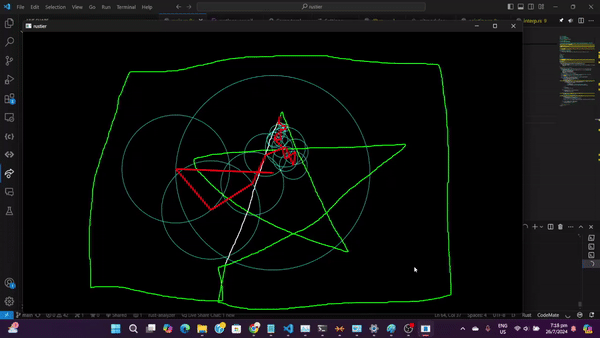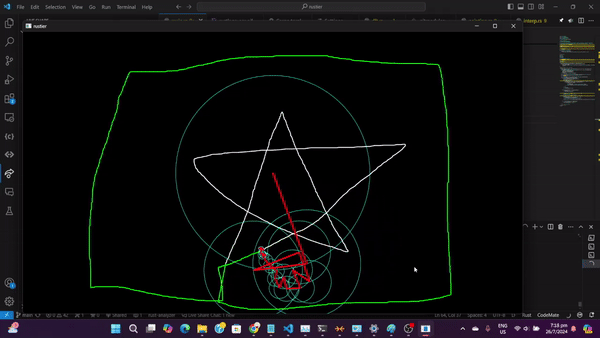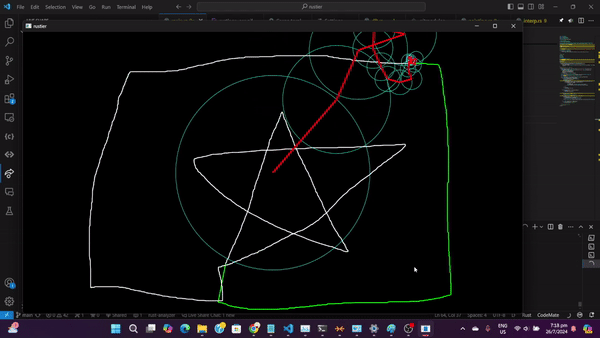
Free Drawing Interface

Cách Hoạt Động Của Visualization

Input: Bạn có thể load file SVG hoặc vẽ tự do bằng chuột
Preprocessing: Đường vẽ được chuyển thành chuỗi điểm phức và resample đều
DFT: Thuật toán DFT tính toán các hệ số Fourier
Visualization:
- Mỗi hệ số Fourier tương ứng với một vòng tròn
- Vòng tròn có bán kính = |hệ số| (magnitude)
- Vòng tròn quay với tốc độ tỷ lệ với tần số k
- Điểm cuối cùng của chuỗi vòng tròn vẽ ra đường cong gốc

Điểm Học Được

Dự án này minh họa những điều quan trọng về DFT:

DFT không chỉ là lý thuyết: Nó có thể tạo ra những ứng dụng thú vị và trực quan
Quan hệ giữa miền thời gian và tần số: Mỗi vòng tròn đại diện cho một tần số, và tổng hợp chúng tạo ra tín hiệu gốc
Tầm quan trọng của preprocessing: Việc resample dữ liệu đầu vào ảnh hưởng lớn đến chất lượng kết quả
Hiệu quả tính toán: Với 2000 vòng tròn, việc tính toán real-time đòi hỏi tối ưu hóa, dùng FFT để hiệu quả hơn.

Thư viện

Code mình sử dụng:

Rust: Ngôn ngữ an toàn và hiệu suất cao
Piston: Game engine cho graphics và user interaction
num crate: Để xử lý số phức
Custom SVG parser: Để đọc file SVG thành điểm

Tham khảo