Error detection - Kiểm soát lỗi (phần 2)
III. Các phương pháp phát hiện lỗi (tiếp)
2. Checksum - tính tổng kiểm tra
Checksum là một phương pháp phát hiện lỗi cơ bản và rộng rãi được sử dụng trong nhiều giao thức truyền thông. Phương pháp này thực hiện việc tính tổng của các đơn vị dữ liệu, thường là các byte hoặc word. Giá trị sum này sau đó sẽ được gửi kèm cùng với dữ liệu. Sau khi nhận, dữ liệu được tính tổng lại và so sánh với tổng đã gửi. Khi xảy ra sự khác biệt cũng đồng nghĩa rằng dữ liệu đã bị thay đổi trong quá trình truyền và xảy ra lỗi.
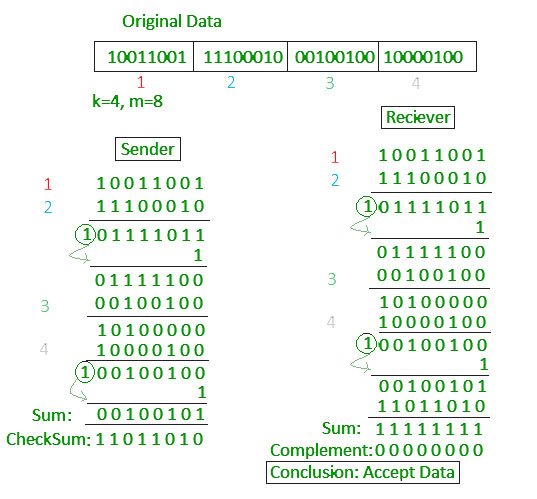
Xét ví dụ chuỗi bit dữ liệu được gửi là , được chia thành đoạn (segment), mỗi đoạn bit.
Phía gửi (Sender) thực hiện sinh mã checksum: Thực hiện phép toán cộng giữa đoạn bit và . Kết quả thu được , dư bit bên trái tiếp tục cộng vào kết quả thu được . Kết quả này tiếp tục được thực hiện phép toán cộng với đoạn bit , kết quả thu được thực hiện tiếp phép toán cộng với đoạn bit , cho tới khi kết thúc chuỗi dữ liệu gửi (Trong quá trình nếu có bit dư ra sẽ mang cộng với kết quả). Cuối cùng thu được kết quả , đảo bit kết quả này chính là mã checksum .
Phía nhận (Receiver) thực hiện tương tự phía gửi, kết quả cuối cùng (không đảo bit như phía gửi) sẽ mang cộng với mã checksum nhận được, nếu thu được kết quả nghĩa là dữ liệu hợp lệ, ngược lại là đã xảy ra lỗi.
Chi tiết các bước bạn đọc có thể theo dõi qua hình ảnh sau:
Chương trình Python sau minh họa cho quá trình sinh mã checksum ở phía gửi:
def calculate_checksum(data_blocks):
sum = '0' * 8 # Quy ước m = 8
for block in data_blocks:
# Hàm binary_addition thực hiện phép cộng các segments (lưu ý bit nhớ)
sum = binary_addition(sum, block)
# Thực hiện đảo bit tại bước cuối cùng
checksum = ''.join('1' if bit == '0' else '0' for bit in sum)
return checksum
Phương pháp checksum khá đơn giản, dễ hiểu, không yêu cầu nhiều tài nguyên nên phù hợp với các giao thức đơn giản. Tuy nhiên, checksum không thực sự an toàn do phép toán module sử dụng trong quá trình tính toán, có thể xảy ra trường hợp các bit "triệt tiêu" lẫn nhau.
Một bài tập nhỏ dành cho bạn đọc: Hãy tính mã checksum của chuỗi bit sau để xem có điều gì đặc biệt nhé:
Ngoài ra, phương pháp checksum được thiết kế chỉ để phát hiện lỗi, nên không thể biết chính xác vị trí của bit lỗi cũng như số lượng bit bị lỗi.
3. Cyclic redundancy check (CRC) - Kiểm tra dư thừa vòng
Cyclic redundancy check là một kỹ thuật phức tạp hơn, cung cấp mức độ bảo vệ cao hơn so với sumcheck hoặc parity check. Phương pháp thực hiện dựa trên mã CRC, còn được gọi là mã đa thức. CRC coi các dãy bit dữ liệu thành hệ số của đa thức, từ đó có thể thực hiện các phép toán trên đa thức (có các hệ số hoặc ) thay thế việc thao tác bit. Các phép toán trên CRC đều không tính "nhớ" (cho phép cộng) hoặc "mượn" (cho phép trừ), thực tế phép cộng và trừ ở đây chính là phép XOR, ví dụ:
Đối với phép nhân và chia, các phép cộng và trừ trong đó đều được thay thế bởi phép XOR.
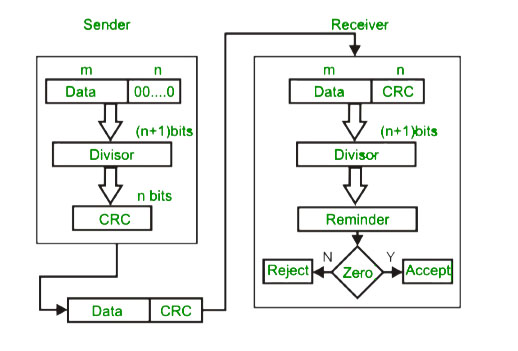
Cyclic redundancy check hoạt động như sau:
- Đầu tiên, hai bên gửi và nhận cần thống nhất một đa thức sinh (CRC generator) có bit cao nhất là .
- Giả sử đa thức sinh có bit, trước hết bên gửi cần ghép thêm bit vào sau dữ liệu gửi. bit này là vị trí của dư trong phép tính sẽ thực hiện ở bước sau.
- Thực hiện phép chia dữ liệu gửi (có thêm bit theo sau) cho đa thức sinh thu được dư (dài bit).
- Đặt vào bit cuối dữ liệu gửi (vị trí bit ) thu được dữ liệu cần gửi.
- Bên nhận thực hiện chia dữ liệu nhận được cho đa thức sinh, nếu kết quả chia hết tức là quá trình truyền tải an toàn, ngược lại thì lỗi đã xảy ra.
Sơ đồ hoạt động của thuật toán như sau:
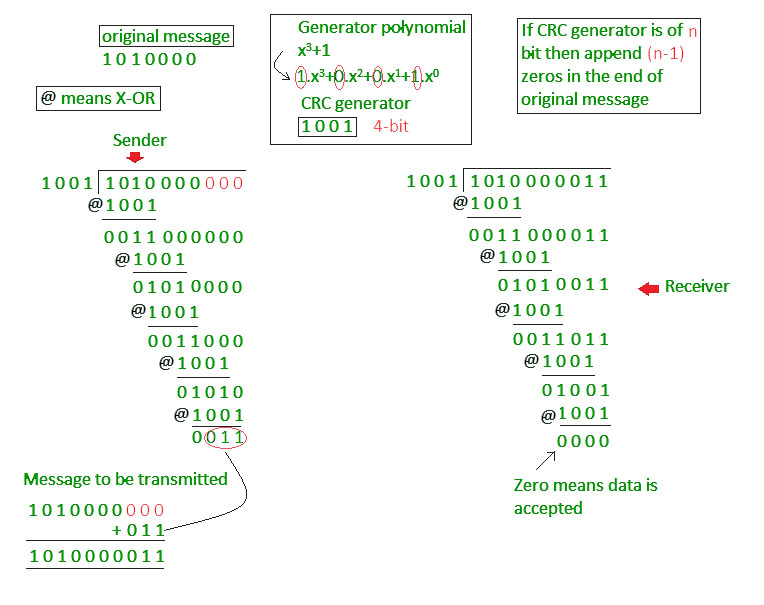
Chúng ta xem xét một ví dụ cụ thể hơn. Dữ liệu cần gửi là chuỗi bit , đa thức sinh quy ước là tương ứng với .
- Bên gửi thêm bit vào sau thu được .
- Thực hiện phép chia cho thu được dư , thay thế vào vị trí cuối của dữ liệu thu được sẽ được gửi đi.
- Bên nhận kiểm tra lỗi bằng cách thực hiện phép chia cho đa thức sinh , kết quả thu được dư , tức là quá trình gửi an toàn.
Chi tiết các bước tính toán bạn đọc có thể theo dõi trong hình ảnh sau (Ký hiệu @ thay cho phép XOR):
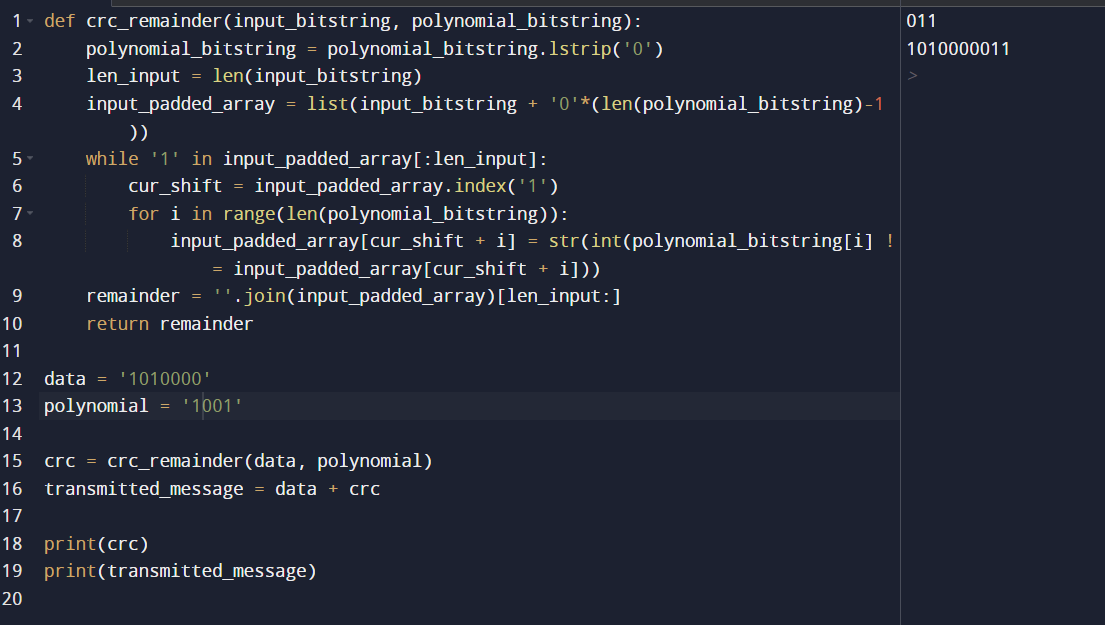
Chương trình Python minh họa cho quá trình tính toán phép chia:
def crc_remainder(input_bitstring, polynomial_bitstring):
polynomial_bitstring = polynomial_bitstring.lstrip('0')
len_input = len(input_bitstring)
input_padded_array = list(input_bitstring + '0'*(len(polynomial_bitstring)-1))
while '1' in input_padded_array[:len_input]:
cur_shift = input_padded_array.index('1')
for i in range(len(polynomial_bitstring)):
input_padded_array[cur_shift + i] = str(int(polynomial_bitstring[i] != input_padded_array[cur_shift + i]))
remainder = ''.join(input_padded_array)[len_input:]
return remainder
Đa thức sinh thường có độ dài hoặc bit. Trong tế bào ATM, CRC bit được sử dụng trong byte tiêu đề. Trong nhiều giao thức thường sử dụng đa thức sinh bit sau:
Cyclic redundancy check được sử dụng rộng rãi trong các giao thức mạng, các thiết bị lưu trữ, và ứng dụng trong việc kiểm tra tính toàn vẹn của dữ liệu bởi tính hiệu quả cao trong việc phát hiện các lỗi phổ biến hoặc các lỗi có mô hình nhất định. Phần cứng hỗ trợ CRC có thể thực hiện kiểm tra lỗi rất nhanh, thậm chí ngay cả trong khi dữ liệu đang được truyền đi, không làm chậm tốc độ truyền dữ liệu. Sự đa dạng của các đa thức sinh CRC cho phép tùy chỉnh mức độ phức tạp của thuật toán để phù hợp với yêu cầu cụ thể của ứng dụng.
Tuy nhiên CRC chỉ phát hiện lỗi nhưng không sửa được chúng, cần kết hợp cơ chế khác như ARQ (Automatic Repeat reQuest) để sửa lỗi khi phát hiện lỗi thông qua CRC. Ngoài ra, khi sử dụng đa thức sinh có bậc cao để tăng độ tin cậy, độ phức tạp của thuật toán cũng tăng lên, yêu cầu nhiều tài nguyên tính toán hơn.
4. So sánh
| Tính năng / Phương pháp | Checksum | Parity (Single & Multiple) | CRC |
|---|---|---|---|
| Độ phức tạp | Thấp | Rất thấp | Cao |
| Hiệu suất | Trung bình | Thấp | Cao |
| Khả năng phát hiện lỗi | Tốt với lỗi nhỏ | Chỉ lỗi đơn giản | Xuất sắc với nhiều loại lỗi |
| Phát hiện lỗi nhiều bit | Trung bình | Kém (chỉ Parity Multiple) | Cao |
| Chi phí tính toán | Thấp | Thấp nhất | Trung bình đến cao |
| Độ tin cậy | Trung bình | Thấp | Cao |
| Ứng dụng | Truyền thông đơn giản | Thiết bị lưu trữ đơn giản | Truyền thông và lưu trữ dữ liệu hiệu suất cao |
Tài liệu tham khảo
- https://www.geeksforgeeks.org/error-detection-in-computer-networks/
- https://csc-knu.github.io/sys-prog/books/Andrew%20S.%20Tanenbaum%20-%20Computer%20Networks.pdf
- https://www.ucg.ac.me/skladiste/blog_44233/objava_64433/fajlovi/Computer%20Networking%20_%20A%20Top%20Down%20Approach,%207th,%20converted.pdf
All rights reserved