Edit Distance

In computer science, edit distance is a way to determine how dissimilar two strings are to one another by counting the minimum number of operations needed to transform one string into the other. Edit distanceis very useful in natural language processing, where automatic spelling correction can determine suggested corrections for a misspelled word by selecting words from a dictionary that have a minimum distance to the word in progress.

Different definitions of an edit distance use different sets of string operations. The usual distance operations are the removal, insertion, or substitution of a character in the string. Being the most common metric, the Levenshtein distance is usually what is meant by "edit distance".

Minimum Edit Distance

Minimum Edit distance between two strings str1 and str2 is defined as the minimum number of insert/delete/substitute operations required to transform str1 into str2. For example if str1 = "ab", str2 = "abc" then making an insert operation of character 'c' on str1 transforms str1 into str2. Therefore, edit distance between str1 and str2 is 1. You can also calculate edit distance as number of operations required to transform str2 into str1. For above example, if we perform a delete operation of character 'c' on str2, it is transformed into str1 resulting in same edit distance of 1.

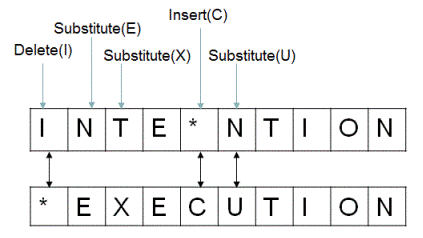
Looking at another example, if str1 = "INTENTION" and str2 = "EXECUTION", then the minimum edit distance between str1 and str2 turns out to be 5 as shown below. All operations are performed on str1.

Algorithm

We can use bottom up approach to compute the edit distance between str1 and str2. We start by computing edit distance for smaller sub-problems and use the results of these smaller sub-problems to compute results for sub-sequent larger problems. The results are stored in a two dimensional array as shown below.

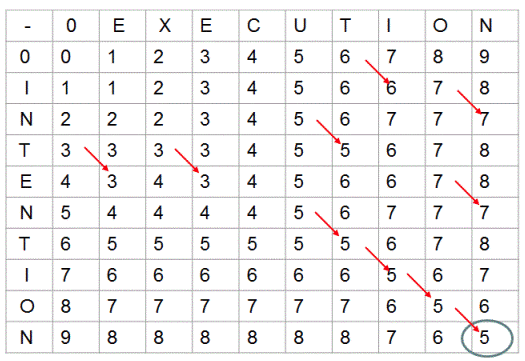
Each cell (m,n) of this array represents distance first 'm' characters of str1 and first 'n' characrers of str2. For example, when 'm' is 0, distance between str1 which is of 0 length and str2 of 'n' length is 'n'. Please observe 0th row of above matrix. Same is the case for values in 0th column where str2 is of 0 length.

Now in this matrix, for cell (m,n) which represents distance between str1 of length 'm' characters and str2 of length 'n' characters, if 'm'th character of str1 and 'n'th character of str2 are same, then we simply need to fill cell(m,n) using value of cell (m-1, n-1) which represents edit distance between first 'm-1' characters if str1 and first 'n-1' characters of str2. Notice the red arrows in the above array.

If 'm'th character of str1 is not equal to 'n'th character of str2, then we choose minimum value from following three cases-

1. Delete 'm'th character of str1 and compute edit distance between 'm-1' characters of str1 and 'n' characters of str2. For this computation, we simply have to do - (1 + array[m-1][n]) where 1 is the cost of delete operation and array[m-1][n] is edit distance between 'm-1' characters of str1 and 'n' characters of str2.
2. Similarly, for the second case of inserting last character of str2 into str1, we have to do - (1 + array[m][n-1]).
3. And for the third case of substituting last character of str1 by last character of str2 we use - (1 + array[m-1][n-1]).

Implementation

The ruby implementation is given below

    def edit_distance str1, str2
        r = str1.length
        c = str2.length
        distanceTable = Array.new(n){Array.new(m)}
        
        (0...r).to_a.each do |m|
             (0...c).to_a.each do |n|
                next distanceTable[m][n] = n if m == 0
                next distanceTable[m][n] = m if n == 0
                next distanceTable[m][n] = distanceTable[m-1][n-1] if str1[m-1][n-1]
                 distanceTable[m][n] = [
                                                1 + distanceTable[m-1][n],
                                                1 + distanceTable[m][n-1],
                                                1 + distanceTable[m-1][n-1]
                                              ].min
            end
        end
        distanceTable[r-1][c-1]
    end

Hope it helps. See you in the future.

For further study: https://web.stanford.edu/class/cs124