10.5K 783 122

Đã đăng vào thg 9 22, 2021 7:57 SA 20 phút đọc

64.8K

Đệ quy và giải thuật đệ quy

I. Từ Quy nạp Toán học...

Trước tiên, cùng xem xét bài toán chứng minh sau: Chứng minh đẳng thức dưới đây đúng với mọi $n \in N^{*}:$

$1+3+5+\cdots+(2n - 1) = n^2 \ (1)$

Ở bậc trung học cơ sở, ta đã biết về phương pháp quy nạp toán học dùng để chứng minh một đẳng thức hoặc bất đẳng thức đúng. Áp dụng phương pháp này, ta có thể giải quyết bài toán trên một cách dễ dàng:

Bước $1$ : Chứng minh đẳng thức đúng với $n = 1$ : Ta thấy $1 = 1^2,$ do đó đẳng thức đúng với $n = 1$ .
Bước $2$ : Lập giả thiết quy nạp - Giả sử đẳng thức đúng với $n = k \ge 1$ : Tức là ta có: $1 + 3 + 5 + \cdots + (2k - 1) = k^2 \ (2)$ .
Bước $3$ : Ta chứng minh đẳng thức đúng với $n = k + 1,$ tức là cần chứng minh:

$1 + 3 + 5 + \cdots + (2k - 1) + [2.(k + 1) - 1] = (k + 1)^2$

Thật vậy, từ đẳng thức $(2)$ ta có:

$1 + 3 + 5 + \cdots + (2k - 1) + [2.(k + 1) - 1] = k^2 + [2.(k + 1) - 1]$

$= k^2 + 2k + 1 = (k + 1)^2$

Vậy đẳng thức $(1)$ đúng với $n = k+1,$ tức là nó đúng với mọi $n \in N^{*}$ .

Một cách tổng quát, quy nạp toán học là việc chứng minh một tính chất nào đó ứng với các số tự nhiên bằng cách chứng minh tính chất đó đúng với một vài trường hợp cơ sở (thường là chứng minh nó đúng với $0$ hoặc $1$ ), sau đó chứng minh nó đúng với $n$ bất kỳ nếu như giả sử rằng nó đúng với mọi số tự nhiên nhỏ hơn $n$ . Những bài toán như vậy rất phổ biến không chỉ trong Toán học, mà còn trong Tin học, đặc biệt là trong các bài toán tìm công thức Toán học. Tuy nhiên, chúng ta sẽ nói kĩ hơn về vấn đề này trong một chuyên đề khác.

II. ...Tới giải thuật đệ quy

1. Khái niệm về đệ quy

Ta gọi một đối tượng là có tính đệ quy nếu như nó được định nghĩa thông qua chính nó hoặc thông qua một số đối tượng nhỏ hơn nó nhưng có cùng dạng với nó. Cùng xét vài ví dụ để làm rõ:

Giai thừa của $n \ (n!)$ được định nghĩa như sau:

$n! = \begin{cases}1,&\text{nếu }n=0.\\ (n - 1)! \times n&\text{nếu }n > 0.\end{cases}$

Một số tự nhiên được định nghĩa như sau:
- $0$ là số tự nhiên.
- $n > 0$ là số tự nhiên nếu như $(n - 1)$ là số tự nhiên.

Phương pháp định nghĩa như trên gọi là phương pháp đệ quy. Có rất nhiều đối tượng trong Toán học được định nghĩa theo kiểu như vậy.

2. Giải thuật đệ quy

Một bài toán $P$ được gọi là có tính chất đệ quy khi lời giải của nó có thể đưa về lời giải của bài toán $P'$ nhỏ hơn nó và có dạng giống nó, đồng thời lời giải của $P'$ không cần dùng tới $P$ . Lời giải cho những bài toán như vậy được gọi là giải thuật đệ quy. Bản chất của giải thuật đệ quy là phân tách một bài toán lớn thành những bài toán nhỏ hơn và dễ giải hơn, sau đó tìm cách kết hợp lời giải của các bài toán nhỏ lại thành lời giải cho bài toán lớn ban đầu. Bài toán tìm giai thừa của $n$ ở bên trên chính là một ví dụ cơ bản nhất cho các bài toán có tính chất đệ quy.

Giữa quy nạp toán học và giải thuật đệ quy có một mối quan hệ rất khăng khít: Nếu như ở quy nạp toán học, ta chứng minh một tính chất toán học dựa vào việc chứng minh nó đúng với một số trường hợp cơ sở rồi chứng minh nó đúng với mọi số tự nhiên $n$ dựa trên việc nó đã đúng với mọi số tự nhiên nhỏ hơn $n;$ thì ở giải thuật đệ quy, chúng ta cũng tìm lời giải cho những bài toán cơ sở (thường rất đơn giản) trước, sau đó tìm cách cài đặt sao cho lời giải của bài toán lớn được suy ra từ lời giải của các bài toán nhỏ hơn tương tự như thế.

III. Công thức truy hồi

Như đã nói ở phần trước, với những bài toán có tính chất đệ quy, sau khi phân tách chúng về bài toán nhỏ hơn, chúng ta sẽ có hai nhiệm vụ:

Tìm lời giải cho các bài toán cơ sở.
Kết hợp lời giải của các bài toán con thành bài toán lớn.

Trong khi bước thứ nhất khá đơn giản vì bài toán cơ sở là bài toán có kích thước nhỏ, rất dễ giải, thì bước thứ hai là bước cần có nhiều tư duy hơn. Hệ thức dùng để liên hệ giữa các bài toán nhỏ và bài toán lớn được gọi là công thức truy hồi. Chúng ta gặp rất nhiều những định nghĩa về công thức truy hồi trong Toán học, lấy ví dụ:

Dãy số Fibonaci có công thức truy hồi là $f_n = f_{n - 1} + f_{n - 2} \ (n > 1)$ và hai bài toán cơ sở là $f_0 = 0, f_1 = 1$ .
Dãy số $u_n$ với công thức truy hồi là $u_n = 3.u_{n - 1} \ (n > 1)$ và bài toán cơ sở là $u_1 = 3$ . $...$

Việc xác định công thức truy hồi của một bài toán có bản chất đệ quy là vấn đề quyết định đến việc có thể giải được nó hay không. Các lời giải đệ quy có thể sử dụng hai cách cài đặt là cài đặt đệ quy và cài đặt không đệ quy, ở phần sau chúng ta sẽ cùng nghiên cứu cách cài đặt các hàm đệ quy để giải bài toán có bản chất đệ quy.

IV. Hàm đệ quy và các thành phần của hàm đệ quy

1. Khái niệm về hàm đệ quy

Các lời giải đệ quy cho một bài toán có thể được viết gọn vào trong một hàm, và hàm đó được gọi là hàm đệ quy. Đặc điểm của một hàm đệ quy là luôn luôn có lời gọi lại tới chính nó (thực tế bài toán đệ quy cũng là đi giải lại chính bài toán đó nhưng với kích thước nhỏ hơn):

{Hàm_đệ_quy} ({Danh_sách_tham_số})
{
    {Gọi_lại_hàm_đệ_quy}({Danh_sách_tham_số});
}

Một cách dễ hiểu nhất, chúng ta có thể tưởng tượng hàm đệ quy giống như một vòng lặp. Nếu như vòng lặp sẽ lặp đi lặp lại khối lệnh của nó với một số lần hữu hạn hoặc vô hạn, thì hàm đệ quy cũng sẽ lặp đi lặp lại đoạn mã được viết bên trong nó một số lần hữu hạn hoặc vô hạn, tùy vào cách viết của chúng ta.

2. Các thành phần của một hàm đệ quy

Một hàm đệ quy luôn luôn bao gồm hai phần:

Phần neo: Chính là lời giải cho bài toán cơ sở, cũng là phần thể hiện tính dừng của thuật toán. Khi hàm đệ quy tự gọi lại chính nó tới một thời điểm nhất định thì sẽ phải đạt được phần neo, bởi vì bài toán không thể phân tách ra mãi được mà phải đạt tới một bài toán cơ sở đã có sẵn kết quả. Công việc ở phần neo rất đơn giản, có thể giải trực tiếp mà không cần thông qua bài toán nhỏ hơn nào cả.
Phần đệ quy: Trong trường hợp bài toán chưa thể giải được bằng phần neo, ta sẽ xác định các bài toán con và gọi đệ quy tới các bài toán con đó để giải chúng. Sau khi đã có lời giải của các bài toán con rồi, ta phối hợp chúng lại bằng công thức truy hồi để có được lời giải của bài toán ban đầu. Phần này thể hiện tính quy nạp của thuật toán.

3. Cơ chế hoạt động của một hàm đệ quy

Ta lấy một ví dụ là hàm đệ quy tính $n!$ như sau:

int factorial(int n)
{
    if (n == 0) // Phần neo.
        return 1;
    else // Phần gọi đệ quy.
        return factorial(n - 1) * n;
}

Ở bài toán này, phần neo định nghĩa trước lời giải cho trường hợp $n = 0$ là $1,$ còn đối với các bài toán có $n > 1,$ ta sẽ dùng lời gọi đệ quy để đưa về giải bài toán có kích thước bằng $n - 1$ rồi từ đó tính $n! = (n - 1)! \times n$ . Chẳng hạn, nếu dùng hàm này để tính $3!,$ giải thuật sẽ diễn ra như sau:

Việc giải bài toán $factorial(3)$ sẽ diễn ra trong $6$ từ việc phân rã $factorial(3)$ xuống $factorial(0)$ rồi lần lượt trả ngược kết quả các bài toán nhỏ lên các bài toán lớn hơn đã gọi nó, cho tới khi đạt được kết quả của bài toán ban đầu. Nguyên lí của việc này là do máy tính khi nhận thấy một bài toán chưa được giải ở lời gọi đệ quy, nó sẽ tạm thời lưu bài toán đó vào một ngăn xếp theo chiều từ trên xuống dưới, như vậy các bài toán chưa được giải sẽ xếp chồng lên nhau theo thứ tự bài toán lớn hơn ở dưới, bài toán nhỏ hơn ở trên. Việc giải các bài toán lại được thực hiện từ trên xuống dưới, như vậy bài toán ở bên dưới (là bài toán lớn hơn) sẽ thu nhận được kết quả của bài toán bên trên (là bài toán nhỏ hơn),...Tiếp tục thực hiện như vậy cho tới khi trong ngăn xếp chỉ còn lại một bài toán cuối cùng, đó chính là bài toán gốc.

Đây là một đặc điểm rất thú vị của đệ quy, có ứng dụng rất lớn trong việc thiết kế các giải thuật sau này như: Quay lui, nhánh cận,...

V. Đệ quy đơn và đệ quy nhị phân

Hàm đệ quy cũng có rất nhiều loại khác nhau, trong lập trình nói chung và lập trình C++ nói riêng, ta có thể chia đệ quy làm $6$ loại sau

Đệ quy đơn (đệ quy tuyến tính).
Đệ quy nhị phân.
Đệ quy đuôi.
Đệ quy đa tuyến.
Đệ quy lồng.
Đệ quy tương hỗ.

Thực ra, tên gọi của các loại đệ quy không hề làm thay đổi bản chất của hàm đệ quy, chỉ là chúng sẽ có đôi chút khác nhau về số lượng lời gọi đệ quy trong hàm, hoặc vị trí của lời gọi mà thôi. Dưới đây chúng ta sẽ xem xét hai loại hàm đệ quy đơn giản nhất là đệ quy đơn và đệ quy nhị phân. Những loại đệ quy khác rất ít khi sử dụng đến nên ta sẽ nói đến chúng ở những bài toán cụ thể sau.

1. Đệ quy đơn

Còn gọi là đệ quy tuyến tính. Đây là dạng đệ quy dễ nhất, được sử dụng cực kỳ thường xuyên trong lập trình. Đặc điểm của hàm đệ quy này là chỉ có một lời gọi duy nhất tới chính nó bên trong thân hàm, chẳng hạn như hàm tính giai thừa $n$ mà chúng ta đã biết ở phần trước. Một ví dụ khác nữa là tính tổng các số từ $1$ tới $n,$ ta cũng có thể sử dụng đệ quy tuyến tính như sau:

void total_n(int n)
{
    if (n == 1)
        return 1;
    else 
        return total_n(n - 1) + n;
}

2. Đệ quy nhị phân

Là một dạng đệ quy nâng cấp hơn, trong mỗi hàm đệ quy sẽ có một dòng lệnh gọi lại chính hàm đó $2$ lần. Cùng xem xét bài toán sau: Dãy số Fibonaci được định nghĩa theo công thức:

$f_n = \begin{cases}0,&\text{nếu }n=0.\\ 1, &\text{nếu }n=1.\\ f_{n - 1} + f_{n - 2},&\text{nếu }n > 1.\end{cases}$

Hãy tìm số fibonaci thứ $n?$

Ta thấy số fibonaci là một đối tượng có bản chất đệ quy, do đó ta có thể tìm được số fibonaci thứ $n$ bằng một hàm đệ quy nhị phân như sau:

int fibo_n(int n)
{
    if (n == 0)
        return 0;
    else  if (n == 1)
        return 1;
    else 
        return fibo_n(n - 1) + fibo_n(n - 2);
}

Mặc dù rất đơn giản, nhưng cách cài đặt đệ quy này có một số nhược điểm khiến cho nó không được khuyến khích trong việc lập trình. Muốn biết đệ quy có những ưu điểm - nhược điểm gì và khi nào nên sử dụng hàm đệ quy, cùng sang phần sau của chuyên đề này nhé!

VI. So sánh giữa cài đặt đệ quy và cài đặt không đệ quy

1. Từ bài toán dãy Fibonaci

Mọi bài toán có bản chất đệ quy đều có thể chuyển về cách cài đặt khử đệ quy, bởi vì thực tế các hàm đệ quy sẽ được chương trình dịch chuyển về những mã lệnh không đệ quy trước khi thực hiện. Vì thế, bài toán Fibonaci có thể viết được lại ở dạng không đệ quy sử dụng mảng một chiều như sau:

int fibo_n(int n)
{
    if (n <= 1)
        return n;

    int f[n + 1];
    f[0] = 0, f[1] = 1;
    for (int i = 2; i <= n; ++i)
        f[i] = f[i - 1] + f[i - 2];
		
    return f[n];
}

Nếu nhìn thoáng qua về độ dài thì cả hai giải thuật đệ quy và không đệ quy của bài toán này đều như nhau. Nhưng nếu phân tích về số lần tính toán, thì câu chuyện sẽ trở nên khác đi rất nhiều. Nếu cùng tính giá trị $f(5),$ thì giải thuật không đệ quy chỉ cần mất đúng $6$ bước tính toán, vì kết quả các bài toán sau khi tính xong sẽ được lưu lại luôn trên mảng một chiều, chỉ cần sử dụng luôn để tính toán. Còn đối với giải thuật đệ quy, thì việc phân tách các bài toán con sẽ diễn ra như sau:

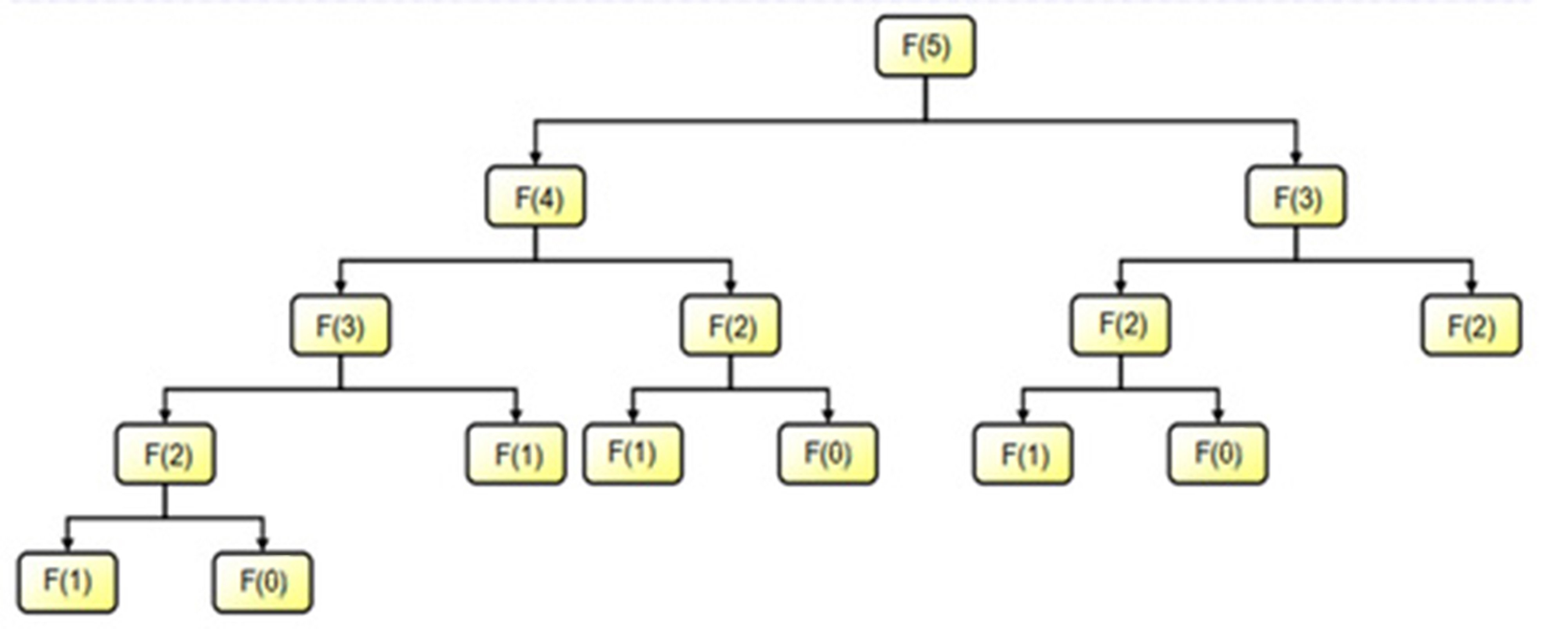
Ta thấy để tính được bài toán $f(5),$ chương trình phải tính lại $1$ lần $f(4), 2$ lần $f(3), 3$ lần $f(2), 5$ lần $f(1)$ và $3$ lần $f(0)$ . Đó gọi là sự xuất hiện của các bài toán con gối nhau, khiến cho chương trình phải tính toán lại nhiều lần một bài toán trong khi đáng lẽ nó chỉ cần tính một lần, từ đó làm cho chương trình chạy rất chậm. Đối với những hàm đệ quy có nhiều lời gọi hơn thì độ phức tạp tính toán sẽ còn tăng lên gấp nhiều lần hơn nữa!

2. Có nên sử dụng đệ quy?

Mặc dù mang trong mình nhược điểm là thời gian thực hiện lớn, nhưng đệ quy không phải là không có ưu điểm. Nhờ vào việc cài đặt đơn giản, ngắn gọn nên giải thuật đệ quy được áp dụng trong nhiều bài toán mà nếu sử dụng lời giải lặp thì rất khó để lập trình, tiêu biểu như giải thuật sắp xếp nhanh (quick sort). Ở một số bài toán phức tạp, việc chuyển giải thuật đệ quy sang giải thuật không đệ quy là việc không đơn giản, cần có sự am hiểu về thuật toán và sự tinh tế nhất định, nên giải thuật đệ quy vẫn luôn luôn có chỗ đứng của nó.

Tuy nhiên, về tổng thể, ta vẫn nên cố gắng hạn chế sử dụng hàm đệ quy ở mức tối đa. Có rất nhiều phương pháp để khử cài đặt đệ quy, tiêu biểu là phương pháp quy hoạch động hoặc phương pháp đệ quy có nhớ mà chúng ta sẽ được học tới ở trong một vài chuyên đề nữa.

VII. Ví dụ minh họa về đệ quy

1. Bài toán giả thuyết Collatz

Collatz đưa ra giả thuyết rằng: Với một số nguyên dương $X,$ nếu $X$ chẵn thì gán $X = \frac{X}{2},$ ngược lại thì gán $X = 3.X + 1$ . Tiếp tục làm như vậy thì sau một số hữu hạn bước, ta sẽ thu được số $1$ .

Cho rằng giả thuyết Collatz là đúng đắn. Vấn đề đặt ra là: Cho trước số nguyên dương $1$ cùng với hai phép toán $\times 2$ và $\text{div } 3$ (với $\text{div}$ là phép chia lấy thương nguyên), hãy sử dụng một cách hợp lý hai phép toán đó để biến số $1$ thành một giá trị nguyên dương $X$ cho trước?

Lấy ví dụ, với $X = 10$ thì ta có:

$1 \times 2 \times 2 \times 2 \times 2 \text{ div } 3 \times 2 = 10$

Dễ dàng nhận thấy, lời giải bài toán gần như là một dãy theo thứ tự ngược lại của phép biến đổi Collatz. Bài toán này là một bài toán có tính đệ quy như sau:

Nếu $X$ là số chẵn, ta tìm cách biểu diễn số $\frac{X}{2}$ rồi viết thêm phép toán $\times 2$ vào cuối.
Nếu $X$ là số lẻ, ta tìm cách biểu diễn số $3.X + 1$ rồi viết thêm phép toán $\text{div } 3$ vào cuối.

Cài đặt:

#include <bits/stdc++.h>
using namespace std;

void recursion(int X)
{
    if (X == 1) // Phần neo.
        cout << X; 
    else 
    {
        if (X % 2 == 0)
        {
            recursion(X / 2); // Gọi đệ quy giải bài toán với X/2.
            
            cout << " * 2 "; // Viết thêm phép toán * 2.
        }
        else 
        {
            recursion(3 * X + 1); // Gọi đệ quy giải bài toán với (3.X + 1).
            
            cout << " div 3 "; // Viết thêm phép toán div 3.
        }
    }
}

int main()
{
    int X;
    cin >> X;
    
    recursion(X);
}

2. Bài toán Tháp Hà Nội

Đây là một bài toán kinh điển được sáng tạo bởi một nhà toán học người Pháp, mà mỗi lập trình viên khi học tới đệ quy đều phải biết đến. Tương truyền rằng tại ngôi đền Benares có ba cái cọc kim cương. Khi khai sinh ra thế giới, thượng đế đặt $N$ cái đĩa bằng vàng chồng lên nhau theo thứ tự giảm dần của đường kính tính từ dưới lên, đĩa to nhất được đặt trên một chiếc cọc.

alt

Các nhà sư lần lượt chuyển các đĩa sang cọc khác theo luật:

Khi di chuyển một đĩa, phải đặt nó vào một trong ba cọc đã cho.
Mỗi lần chỉ có thể chuyển một đĩa và phải là đĩa ở trên cùng của một cọc.
Tại một vị trí, đĩa nào mới chuyển đến sẽ phải đặt lên trên cùng.
Đĩa lớn hơn không bao giờ được phép đặt lên trên đĩa nhỏ hơn.

Ngày tận thế sẽ đến khi toàn bộ chồng đĩa được chuyển sang một cọc khác. Bài toán đặt ra là hãy tìm một phương án chuyển toàn bộ $N$ đĩa ban đầu từ cọc $1$ sang cọc $3?$

Với tư duy quy nạp toán học và sức mạnh của đệ quy, bài toán này có thể được giải quyết dễ dàng như sau:

Xét $N$ đĩa ban đầu đặt ở cọc $1$ . Nếu $N = 1$ thì chuyển đĩa đó từ cọc $1$ sang cọc $3$ là xong.
Ta lấy cọc $3$ làm cọc trung gian. Bài toán được phân tách ra làm hai phần: Chuyển $N - 1$ đĩa từ cọc $1$ sang cọc trung gian $3,$ rồi chuyển đĩa ở cuối cùng sang cọc $2,$ cuối cùng chuyển lại $N - 1$ chiếc đĩa ở cọc $2$ sang cọc $3$ bằng cách lấy cọc $1$ làm trung gian.