Đệ quy đuôi (Tail Recursive Function) trong Scala

Bài đăng này đã không được cập nhật trong 3 năm

Intro

Như chúng ta đã biết đệ quy luôn là một thuật toán hay để xử lý các vấn đề, bài toán liên quan đến tính lập lại, nó giúp code của chúng ta ngắn, dễ nhìn và có thể là dễ hiểu hơn. Tuy vậy không phải lúc nào chúng ta cũng nên sử dụng đệ quy vì sẽ rất khó để quản lý số vòng lặp dẫn đến StackOverFlow. Vì sao lại vậy? Bài viết này sẽ đề cập đến Đệ quy (Recursion), sâu hơn là Đệ quy đuôi (Tail Recursive Function) và tại sao đệ quy đuôi lại được nhắc đến nhiều trong ngôn ngữ Scala.

Đệ quy (Recursion)

Có lẽ chúng ta đều biết đệ quy là gì phải ko? Một hàm gọi chính nó hay hàm A gọi hàm B, hàm B lại gọi lại hàm A hay hàm A gọi hàm B, B gọi C và C lại gọi A, v.v Tựu chung lại đệ quy là một hàm gọi chính nó. Có 2 loại đệ quy chính là đệ quy đầu và đệ quy đuôi. Đệ quy đầu là một hàm sẽ gọi đệ quy rồi mới thực hiện các phép tính khác trong hàm, có thể sử dụng kết quả của phép đệ quy trước đó. Đệ quy đuôi là tất cả phép tính được thực hiện trước rồi mới gọi đệ quy sau cùng. Ví dụ 1 đoạn code đệ quy

def listLength1(list: List[_]): Int = {
  if (list == Nil) 0
  else 1 + listLength1(list.tail)
}

Câu hỏi cho bạn là đây là đệ quy đầu hay đệ quy đuôi. Hàm này thực hiện như sau:

Đầu tiên hàm này sẽ kiểm tra danh sách này có nil không
Nếu có thì trả lại 0
Nếu không nó trả lại 1 cộng với kết quả của một đệ quy khác

Có thể thấy đệ quy là dòng được viết cuối cùng. Vậy đây là đệ quy đuôi? Sai. Vì đệ quy được gọi và sau đó cộng 1 để ra kết quả cuối cùng. Đây chính xác là đệ quy đầu. Chúng ta có thể viết lại hàm này theo cách đệ quy cuối như sau:

def listLength2(list: List[_]): Int = {
  def listLength2Helper(list: List[_], len: Int): Int = {
    if (list == Nil) len
    else listLength2Helper(list.tail, len + 1)
  }
  listLength2Helper(list, 0)
}

Một ví dụ khác rõ hơn để phân biệt đệ quy đầu và đệ cuối (thanks to Nghia le Van @obito)

Giải thuật tính tổng các số nguyên sum(5) = 1 + 2 + 3 + 4 + 5 = 15

Đệ quy đầu sẽ là:

def sum(x)
  if x == 1
    return x
  else
    return x + sum(x - 1)
  end
end

Khi chạy chương trình sẽ được thực hiện như sau:

sum(5)
5 + sum(4)
5 + (4 + sum(3))
5 + (4 + (3 + sum(2)))
5 + (4 + (3 + (2 + sum(1))))
5 + (4 + (3 + (2 + 1)))
15

Lúc gọi sum(5), chương trình phải tính toán sum(4) trước nên sum(5) sẽ được lưu lại trong call stack, sum(4) được gọi, cứ như vậy sum(5), sum(4), sum(3), sum(2) sẽ được lưu lại trong call stack, đến khi sum(1) được gọi trả về kết quả, sum(2), sum(3), sum(4), sum(5) mới được gọi ra từ call stack và trả về kết quả.

Còn đệ quy đuôi sẽ là:

def sum(x, running_total=0):
  if x == 0
    return running_total
  else
    return sum(x - 1, running_total + x)
  end
end

Kết quả chạy:

sum(5, 0)
sum(4, 5)
sum(3, 9)
sum(2, 12)
sum(1, 14)
sum(0, 15)
15

Hạn chế của đệ quy

Nhưng vấn đề gặp phải như đã đề cập ở trên là:

Đệ quy rất khó và không trực quan. Nó không dễ theo dõi như các vòng lặp đơn thuần mà chúng ta có thể nhìn từ trên xuống dưới và hiểu toàn bộ quá trình vòng lặp ấy đang làm gì. Ở đệ quy, bạn chỉ có thể nhìn thấy một lớp và phải tưởng tượng ra các lớp tiếp theo làm gì. Đổi lại thì đệ quy sẽ ngắn hơn nhiều.
Đa phần các ngôn ngữ được thiết kế cho vòng lặp cơ bản, ví như Java sẽ là vòng lặp for-each, while-do, array … Vì vậy sẽ không có tinh chỉnh call stack cho các hàm đệ quy. Đơn giản là khi bạn gọi một hàm thì 1 lớp mới sẽ đc chèn vào call stack. Call stack sẽ là nơi lưu giữ các biến cục bộ của một hàm. Nhưng call stack là có hạn. Đệ quy là tốt khi bạn biết chắc là nó sẽ không lặp lại không quá vài chục lần. Nhưng nếu đệ quy xảy ra quá nhiều tầng thì sẽ không còn đủ stack cho chúng và xảy ra StackOverFlow. Bạn có thể xem ví dụ bên dưới để hiểu rõ hơn.

Đây là 1 đoạn code sử dụng đệ quy để tính hàm giai thừa:

int fact(int n){
  if(n == 0)
    return 1;
  else
    return n * fact(n - 1);
}

Ví dụ fact(5) sẽ được biểu điễn như sau:

(fact 5)
(* 5 (fact 4))
(* 5 (* 4 (fact 3)))
(* 5 (* 4 (* 3 (fact 2))))
(* 5 (* 4 (* 3 (* 2 (fact 1)))))
(* 5 (* 4 (* 3 (* 2 1))))
(* 5 (* 4 (* 3 2)))
(* 5 (* 4 6))
(* 5 24)
120

Đoạn code sẽ đc compiler dịch ra như sau:

      pushl   %ebp                ; *--sp = bp;
      movl    $1, %eax            ; ax = 1;
      movl    %esp, %ebp          ; bp – sp;
      subl    %8, %esp            ; sp -= 2;
      movl    %ebx, -4(ebp)       ; bp[-1] = bx;
      movl    8(%ebp), %ebx       ; bx = bp[2];
      testl   %ebx %ebx           ; if(bx)
      jne     L5                  ; goto L5;
  L1: movl    -4(%ebp), %ebx      ; bx = bp[1];
      movl    %ebp, %esp          ; sp = bp;
      popl    %ebp                ; bp = *sp++;
      ret                         ; goto *sp++;
  L5: leal    -1(%ebx), %eax      ; ax = bx-1;
      movl    %eax, (%esp)        ; *sp = ax;
      call    fact                ; *--sp = next instruction; goto fact;
      imull   %ebx, %eax          ; ax = ax*bx;
      jmp     L1                  ; goto L1;

Và call stack sẽ tiếp tục đầy lên khi mỗi lần đệ quy được gọi:

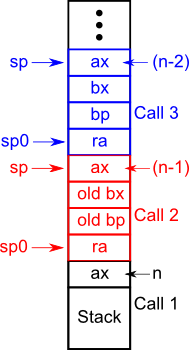
Tại sao lại nhắc đến đệ quy đuôi trong Scala?

Hãy tưởng tượng một hàm đệ quy đuôi khi chạy hết các hàm tính toán của nó và sẵn sàng để gọi đệ quy. Tại thời điểm này chúng ta đâu còn cần những biến cục bộ nữa vì chúng đã được tính toán ở trên hết rồi. Chúng ta không cần biết đang ở lớp nào của đệ quy nữa. Vì vậy trong Scala, đệ quy đuôi được tinh chỉnh để ngăn chặn sự tạo mới của những khung bộ nhớ mới thay vào đó tái sử dụng khung bộ nhớ cũ trong call stack. Và call stack không bao giờ bị đầy lên ngay cả khi đệ quy rất nhiều lần. Điều này tạo nên sự đặc biệt của đệ quy đuôi trong Scala. Trong một số ngôn ngữ khác cũng áp dụng ý tưởng này tuy nhiên sẽ xử lý bằng cách biến đệ quy thành dạng các vòng lặp cơ bản hay còn gọi là khử đệ quy. Và điều này không thể áp dụng được với đệ quy đầu. Vì các phép tính được thực hiện sau khi gọi đệ quy vì chúng ta cần các biến cục bộ đó.

Cách áp dụng tinh chỉnh đệ quy cuối trong Scala

Hai ví dụ listLength1 và listLength2 ở trên là những trường hợp rất cơ bản và dễ dàng nhận thấy đâu là đệ quy cuối. Nhưng không phải bao giờ cũng vậy. Nếu muốn viết một hàm đệ quy phức tạp hơn và bạn muốn nó là một đệ quy cuối. Vậy làm cách nào để biết bạn đã viết đúng dạn đệ quy cuối. Cách duy nhất bạn thường làm là thử trong unit test và bạn phải biết chắc là test với số liệu bao nhiêu để xảy ra StackOverFlow. Scala cung cấp cho bạn 1 đánh dấu để áp dụng tinh chỉnh đệ quy cuối là @tailrec. Đánh dấu này sẽ giúp compiler báo lỗi khi không thực hiện được tinh chỉnh. Ví dụ

def product2(ints: List[Int]): Int = {
  @tailrec
  def productAccumulator(ints: List[Int], accum: Int): Int = {
    ints match {
       case Nil => accum
       case x :: tail => productAccumulator(tail, accum * x)
    }
  }
  productAccumulator(ints, 1)
}