Data Structure & Algorithm - Graph Algorithms - Depth First Search (DFS)

Để giải các bài toán trên đồ thị, chúng ta cần một cơ chế duyệt đồ thị. Giống như thuật toán duyệt cây (Inorder, Preorder, Postorder và Level-Order traverse), các thuật toán tìm kiếm đồ thị bắt đầu từ một số đỉnh nguồn trong đồ thị và tìm kiếm đồ thị bằng cách đi qua các cạnh và đánh dấu các đỉnh. Bây giờ, chúng ta sẽ thảo luận về thuật toán tìm kiếm theo chiều sâu (Depth First Search - DFS),

1. DFS là gì?

Tìm kiếm theo chiều sâu (DFS) là một thuật toán để duyệt qua hoặc tìm kiếm cấu trúc dữ liệu dạng cây hoặc đồ thị. Thuật toán bắt đầu tại nút gốc (chọn một số nút tùy ý làm nút gốc trong trường hợp đồ thị) và kiểm tra từng nhánh càng xa càng tốt trước khi quay lui.

Kết quả của một DFS là một cây bao trùm (spanning tree). Cây khung (spanning tree) là một đồ thị không có vòng lặp. Để thực hiện duyệt theo DFS, chúng ta cần sử dụng cấu trúc dữ liệu ngăn xếp có kích thước tối đa bằng tổng số đỉnh trong biểu đồ.

2. Thuật toán

Để cài đặt DFS, ta cần thực hiện các bước sau:

Lấy một đỉnh bất kỳ trong đồ thì đưa vào ngăn xếp.
Lấy top value của ngăn xếp để duyệt và thêm vào visited list.
Tạo một list bao gồm các đỉnh liền kề của đỉnh đang xét, thêm những đỉnh không có trong visited list vào ngăn xếp.
Tiếp tục lặp lại bước 2 và bước 3 đến khi ngăn xếp rỗng.

Ví dụ:

Hãy xem thuật toán Tìm kiếm theo chiều sâu hoạt động như thế nào với một ví dụ. Chúng ta dùng đồ thị vô hướng có 5 đỉnh. 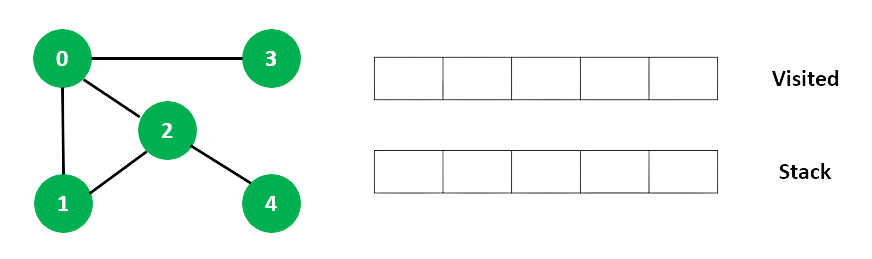Chúng ta bắt đầu từ đỉnh 0, thuật toán DFS bắt đầu bằng cách đứa nó vào danh sách Visited và đưa tất cả các cạnh liền kề đỉnh đang xét vào ngăn xếp. 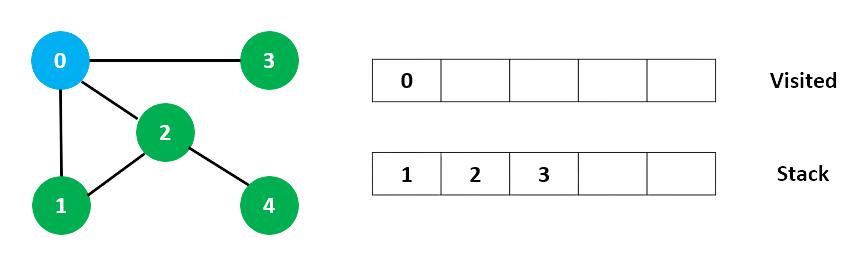Tiếp theo, chúng ta truy cập phần tử ở đầu ngăn xếp tức là 1 và đi đến các nút liền kề của nó. Vì 0 đã được truy cập, nên 2 là số được xét. 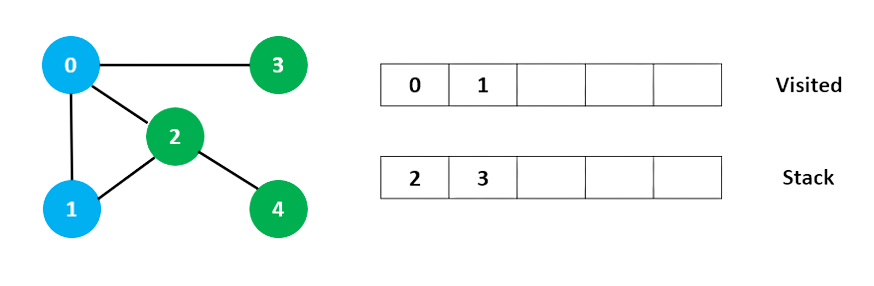Đỉnh 2 có một đỉnh liền kề chưa được thăm là 4, vì vậy chúng ta thêm đỉnh đó vào vị trí đầu của ngăn xếp và duyệt nó. 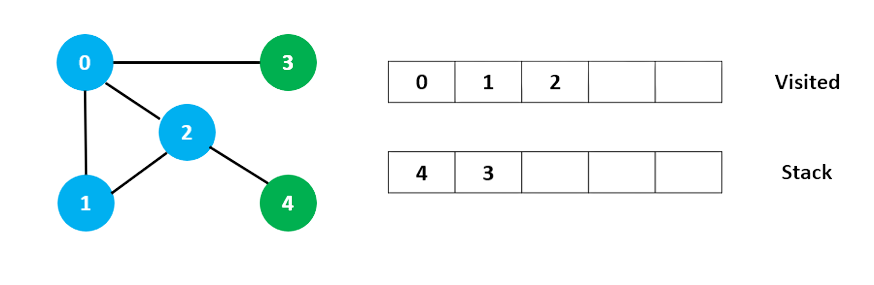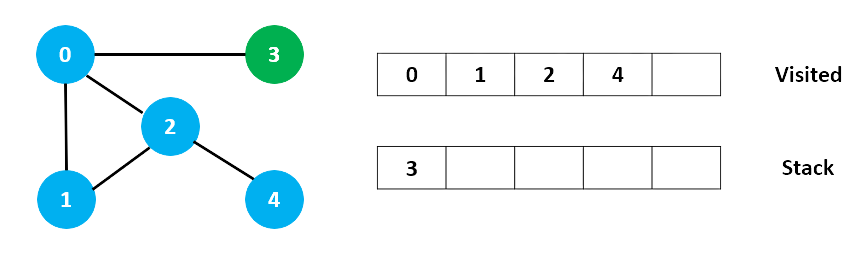Sau khi chúng ta duyệt phần tử 3 cuối cùng, nó không có bất kỳ nút liền kề nào chưa được duyệt, vì vậy chúng tôi đã hoàn thành tìm kiếm theo chiều sâu trong đồ thị trên.

3. Cài đặt

import java.util.Stack;

class Vertex {
        public char label;
        public boolean visited;

        public Vertex(char label) {
            this.label = label;
            this.visited = false;
        }
}

class myGraphDFS {
    private final int maxVertices = 20;
    private Vertex vertexList[];
    private int adjMatrix[][];
    private int vertexCount;
    private Stack<Integer> theStack;

    public myGraphDFS() {
        vertexList = new Vertex[maxVertices];
        adjMatrix = new int[maxVertices][maxVertices];
        vertexCount = 0;
        for (int y = 0; y < maxVertices; y++) {
            for (int x = 0; x < maxVertices; x++) {
                adjMatrix[x][y] = 0;
            }
        }
        theStack = new Stack<>();
    }

    public void addVertex(char label) {
        vertexList[vertexCount++] = new Vertex(label);
    }

    public void addEdge(int start, int end) {
        adjMatrix[start][end] = 1;
        adjMatrix[end][start] = 1;
    }

    public void displayVertex(int v) {
        System.out.print(vertexList[v].label + " ");
    }

    public void dfs() {
        vertexList[0].visited = true;
        displayVertex(0);
        theStack.push(0);

        while (!theStack.isEmpty()) {
            // get an unvisited vertex adjacent to stack top
            int v = getAdjUnvisitedVertex(theStack.peek());
            if (v == -1) {
                theStack.pop();
            } else {
                vertexList[v].visited = true;
                displayVertex(v);
                theStack.push(v);
            }
        }

        for (int j = 0; j < vertexCount; j++) {
            vertexList[j].visited = true;
        }
    }

    public int getAdjUnvisitedVertex(int v) {
        for (int j = 0; j < vertexCount; j++) {
            if (adjMatrix[v][j] == 1 && vertexList[j].visited == false) {
                return j;
            }
        }
        return -1;
    }

    public static void main(String[] args) {
        myGraphDFS g = new myGraphDFS();
        g.addVertex('0');
        g.addVertex('1');
        g.addVertex('2');
        g.addVertex('3');
        g.addVertex('4');

        g.addEdge(0, 1);
        g.addEdge(0, 2);
        g.addEdge(0, 3);
        g.addEdge(1, 0);
        g.addEdge(1, 2);
        g.addEdge(2, 0);
        g.addEdge(2, 1);
        g.addEdge(2, 4);
        g.addEdge(3, 0);
        g.addEdge(4, 2);

        g.dfs();
    }
}

4. Độ phức tạp

Độ phức tạp thời gian của thuật toán DFS được biểu diễn dưới dạng O(V + E), trong đó V là số nút và E là số cạnh. Độ phức tạp không gian của thuật toán là O(V).

5. Ứng dụng

Có rất nhiều ứng dụng của thuật toán tìm kiếm theo chiều sâu trong lý thuyết đồ thị. Thuật toán DFS có thể được sử dụng để giải hầu hết các bài toán liên quan đến đồ thị hoặc cây. Một số ứng dụng phổ biến của nó là:

Sắp xếp tô pô, schedule problems, phát hiện chu trình trong biểu đồ và giải các câu đố chỉ bằng một giải pháp, chẳng hạn như mê cung hoặc câu đố sudoku, tất cả đều sử dụng tìm kiếm theo chiều sâu.
Các ứng dụng khác liên quan đến phân tích mạng, chẳng hạn như phát hiện xem biểu đồ có phải là bipartite không.
DFS cũng được sử dụng như một chương trình con trong các thuật toán matching trong lý thuyết đồ thị như thuật toán Hopcroft-Karp.
Tìm kiếm theo chiều sâu được sử dụng trong lập route mapping, scheduling và tìm cây khung.

Nguồn:

Web