1. Giới thiệu

Đôi khi dữ liệu chúng ta lưu trữ hoặc truy xuất trong một ứng dụng có thể có ít hoặc không có thứ tự. Chúng ta có thể phải sắp xếp lại dữ liệu để xử lý chính xác hoặc sử dụng nó một cách hiệu quả. Trong những năm qua, các nhà khoa học máy tính đã tạo ra nhiều thuật toán sắp xếp để tổ chức dữ liệu.

Bài viết này chúng ta sẽ xem xét các thuật toán sắp xếp phổ biến, chúng ta chắc cũng đã quen với những thuật toán sắp xếp khi còn ngồi trên ghế nhà trường, cùng hiểu cách chúng hoạt động và mã hóa chúng trong Python. Chúng tôi cũng sẽ so sánh cách sắp xếp nào nhanh hơn các items trong một list. Để đơn giản, việc triển khai thuật toán sẽ sắp xếp danh sách các số theo thứ tự tăng dần. Chúng ta có những thuật toán sắp xếp phổ biến sau:

• Bubble Sort
• Selection Sort
• Insertion Sort
• Merge Sort
• Heap Sort
• Quick Sort
• Sorting in Python

2. Bubble Sort

Thuật toán sắp xếp đơn giản này lặp lại qua một danh sách, so sánh các phần tử theo cặp và hoán đổi chúng cho đến khi các phần tử lớn hơn "nổi bong bóng" đến cuối danh sách và các phần tử nhỏ hơn nằm ở "dưới cùng".

giải thích

Chúng ta bắt đầu bằng cách so sánh hai elements đầu tiên của danh sách. Nếu phần tử đầu tiên lớn hơn phần tử thứ hai, chúng ta hoán đổi chúng. Nếu họ đã theo thứ tự, chúng ta giữ nguyên. Sau đó chúng tôi chuyển sang cặp phần tử tiếp theo, so sánh giá trị của chúng và trao đổi khi cần thiết. Quá trình này tiếp tục đến cặp mục cuối cùng trong danh sách.

Khi đến cuối danh sách, nó lặp lại quy trình này cho mọi mục. Mặc dù, điều này là không hiệu quả cao. Điều gì nếu chỉ một hoán đổi duy nhất cần phải được thực hiện trong mảng? Tại sao chúng ta vẫn lặp đi lặp lại ^2 lần, mặc dù nó đã được sắp xếp? Rõ ràng, để tối ưu hóa thuật toán, chúng ta cần dừng nó khi sắp xếp xong.

Làm thế nào chúng ta biết rằng chúng ta đã sắp xếp xong? Nếu các mục theo thứ tự thì chúng ta sẽ không phải tráo đổi các items. Vì vậy, bất cứ khi nào chúng ta hoán đổi giá trị, chúng ta đặt flag thành True để lặp lại quá trình sắp xếp. Nếu không có swapped xảy ra, flag sẽ vẫn là Sai và thuật toán sẽ dừng lại.

def bubble_sort(nums):  
    # We set swapped to True so the loop looks runs at least once
    swapped = True
    while swapped:
        swapped = False
        for i in range(len(nums) - 1):
            if nums[i] > nums[i + 1]:
                # Swap the elements
                nums[i], nums[i + 1] = nums[i + 1], nums[i]
                # Set the flag to True so we'll loop again
                swapped = True


# Verify it works
random_list_of_nums = [5, 2, 1, 8, 4]  
bubble_sort(random_list_of_nums)  
print(random_list_of_nums) 

Thuật toán chạy trong một vòng lặp while, chỉ phá vỡ khi không có mục nào được hoán đổi. Chúng ta đã đặt swapped thành True ngay từ đầu để đảm bảo thuật toán chạy ít nhất một lần.

Độ phức tạp thời gian

Trong trường hợp xấu nhất (khi danh sách theo thứ tự ngược lại), thuật toán này sẽ phải hoán đổi mọi item của mảng. flag swapper của chúng ta sẽ được đặt thành True trên mỗi lần lặp. Do đó, nếu chúng ta có n phần tử trong danh sách của mình, chúng ta sẽ có n lần lặp cho mỗi mục - do đó độ phức tạp thời gian của Bubble Sort là O (n ^ 2).

3. Selection Sort

Thuật toán này phân chia danh sách thành hai phần: được sắp xếp và chưa được sắp xếp. Chúng ta liên tục xóa phần tử nhỏ nhất của phân đoạn chưa sắp xếp của danh sách và nối nó vào phân đoạn đã sắp xếp.

giải thích

Trong thực tế, chúng ta không cần tạo một danh sách mới cho các phần tử được sắp xếp, những gì chúng ta làm là coi phần ngoài cùng bên trái của danh sách là phân đoạn được sắp xếp. Sau đó chúng ta tìm kiếm phần tử nhỏ nhất trong toàn bộ danh sách đã cho và hoán đổi nó với phần tử đầu tiên.

def selection_sort(nums):  
    # This value of i corresponds to how many values were sorted
    for i in range(len(nums)):
        # We assume that the first item of the unsorted segment is the smallest
        lowest_value_index = i
        # This loop iterates over the unsorted items
        for j in range(i + 1, len(nums)):
            if nums[j] < nums[lowest_value_index]:
                lowest_value_index = j
        # Swap values of the lowest unsorted element with the first unsorted
        # element
        nums[i], nums[lowest_value_index] = nums[lowest_value_index], nums[i]


# Verify it works
random_list_of_nums = [12, 8, 3, 20, 11]  
selection_sort(random_list_of_nums)  
print(random_list_of_nums)  

Chúng tôi thấy rằng khi i tăng lên, chúng ta cần phải kiểm tra ít tiems hơn.

Độ phức tạp thời gian

Chúng ta có thể dễ dàng có được độ phức tạp thời gian bằng cách kiểm tra các vòng lặp trong thuật toán Sắp xếp lựa chọn. Đối với một danh sách có n phần tử, vòng lặp ngoài lặp lại n lần. Vòng lặp bên trong lặp lại n-1 khi i bằng 1, và sau đó n-2 vì i bằng 2 và cứ thế.

Số lượng so sánh là (n - 1) + (n - 2) + ... + 1, điều này mang lại cho Lựa chọn Sắp xếp độ phức tạp thời gian của O (n ^ 2).

4. Insertion Sort

Giống như Lựa chọn Sắp xếp, thuật toán này phân chia danh sách thành các phần được sắp xếp và chưa sắp xếp. Nó lặp lại trên phân đoạn chưa sắp xếp và chèn phần tử đang được xem vào vị trí chính xác của danh sách được sắp xếp.

giải thích

Chúng ta giả định rằng phần tử đầu tiên của danh sách được sắp xếp. Sau đó chúng ta đi đến phần tử tiếp theo, hãy gọi nó là x. Nếu x lớn hơn phần tử đầu tiên, chúng ta để nguyên. Nếu x nhỏ hơn, chúng ta sao chép giá trị của phần tử đầu tiên sang vị trí thứ hai và sau đó đặt phần tử đầu tiên thành x.

Khi chúng ta đi đến các phần tử khác của phân đoạn chưa được sắp xếp, chúng ta liên tục di chuyển các phần tử lớn hơn trong phân đoạn được sắp xếp lên danh sách cho đến khi chúng ta gặp một phần tử nhỏ hơn x hoặc đến cuối đoạn được sắp xếp, sau đó đặt x vào vị trí chính xác.

def insertion_sort(nums):  
    # Start on the second element as we assume the first element is sorted
    for i in range(1, len(nums)):
        item_to_insert = nums[i]
        # And keep a reference of the index of the previous element
        j = i - 1
        # Move all items of the sorted segment forward if they are larger than
        # the item to insert
        while j >= 0 and nums[j] > item_to_insert:
            nums[j + 1] = nums[j]
            j -= 1
        # Insert the item
        nums[j + 1] = item_to_insert


# Verify it works
random_list_of_nums = [9, 1, 15, 28, 6]  
insertion_sort(random_list_of_nums)  
print(random_list_of_nums) 

Độ phức tạp thời gian

Trong trường hợp xấu nhất, một mảng sẽ được sắp xếp theo thứ tự ngược lại. Vòng lặp for bên ngoài trong chức năng Sắp xếp chèn luôn lặp lại n-1 lần.

Trong trường hợp xấu nhất, vòng lặp for bên trong sẽ hoán đổi một lần, sau đó hoán đổi hai lần và cứ thế. Số lượng giao dịch hoán đổi sau đó sẽ là 1 + 2 + ... + (n - 3) + (n - 2) + (n - 1), điều này mang lại cho Sắp xếp chèn một độ phức tạp thời gian của O (n ^ 2).

5. Heap Sort

Thuật toán sắp xếp phổ biến này, như sắp xếp Chèn và Chọn, phân đoạn danh sách thành các phần được sắp xếp và chưa sắp xếp. Nó chuyển đổi phân đoạn chưa sắp xếp của danh sách thành cấu trúc dữ liệu Heap, để chúng ta có thể xác định hiệu quả phần tử lớn nhất.

giải thích

Chúng ta bắt đầu bằng cách chuyển đổi danh sách thành Max Heap - Cây nhị phân trong đó phần tử lớn nhất là nút gốc. Sau đó chúng tôi đặt mục đó vào cuối danh sách. Sau đó, chúng ta xây dựng lại Heap Max của chúng ta hiện có một giá trị nhỏ hơn, đặt giá trị lớn nhất mới trước mục cuối cùng của danh sách. Chúng tôi lặp lại quá trình xây dựng heap này cho đến khi tất cả các nút được loại bỏ.

def heapify(nums, heap_size, root_index):  
    # Assume the index of the largest element is the root index
    largest = root_index
    left_child = (2 * root_index) + 1
    right_child = (2 * root_index) + 2

    # If the left child of the root is a valid index, and the element is greater
    # than the current largest element, then update the largest element
    if left_child < heap_size and nums[left_child] > nums[largest]:
        largest = left_child

    # Do the same for the right child of the root
    if right_child < heap_size and nums[right_child] > nums[largest]:
        largest = right_child

    # If the largest element is no longer the root element, swap them
    if largest != root_index:
        nums[root_index], nums[largest] = nums[largest], nums[root_index]
        # Heapify the new root element to ensure it's the largest
        heapify(nums, heap_size, largest)


def heap_sort(nums):  
    n = len(nums)

    # Create a Max Heap from the list
    # The 2nd argument of range means we stop at the element before -1 i.e.
    # the first element of the list.
    # The 3rd argument of range means we iterate backwards, reducing the count
    # of i by 1
    for i in range(n, -1, -1):
        heapify(nums, n, i)

    # Move the root of the max heap to the end of
    for i in range(n - 1, 0, -1):
        nums[i], nums[0] = nums[0], nums[i]
        heapify(nums, i, 0)


# Verify it works
random_list_of_nums = [35, 12, 43, 8, 51]  
heap_sort(random_list_of_nums)  
print(random_list_of_nums)  

Độ phức tạp thời gian

Trước tiên chúng ta hãy xem xét độ phức tạp thời gian của hàm heapify. Trong trường hợp xấu nhất, phần tử lớn nhất không bao giờ là phần tử gốc, điều này gây ra một lệnh gọi đệ quy để heapify. Trong khi các cuộc gọi đệ quy có vẻ expensive, hãy nhớ rằng chúng ta đang làm việc với cây nhị phân.

Hình dung một cây nhị phân có 3 phần tử, nó có chiều cao là 2. Bây giờ hãy hình dung một cây nhị phân có 7 phần tử, nó có chiều cao là 3. Cây phát triển logarit theo n. Hàm heapify đi ngang qua cây đó trong thời gian O (log (n)).

Hàm heap_sort lặp lại qua mảng n lần. Do đó, độ phức tạp thời gian tổng thể của thuật toán Heap Sort là O (nlog (n)).

6. Merge Sort

Thuật toán phân chia và trị này chia một danh sách thành một nửa và tiếp tục chia danh sách cho 2 cho đến khi nó chỉ có các phần tử số ít. Các phần tử liền kề trở thành các cặp được sắp xếp, sau đó các cặp được sắp xếp cũng được merge và sắp xếp với các cặp khác. Quá trình này tiếp tục cho đến khi chúng ta nhận được một danh sách được sắp xếp với tất cả các yếu tố của danh sách đầu vào chưa được sắp xếp.

giải thích

Chúng ta đệ quy chia danh sách thành một nửa cho đến khi chúng ta có danh sách với kích thước = một. Sau đó chúng ta merge từng nửa được tách ra, sắp xếp chúng trong quá trình.

Sắp xếp được thực hiện bằng cách so sánh các yếu tố nhỏ nhất của mỗi nửa. Yếu tố đầu tiên của mỗi danh sách là yếu tố đầu tiên được so sánh. Nếu nửa đầu bắt đầu với giá trị nhỏ hơn, thì chúng ta thêm nó vào danh sách đã sắp xếp. Sau đó, chúng ta so sánh giá trị nhỏ thứ hai của nửa đầu với giá trị nhỏ nhất đầu tiên của nửa thứ hai.

Mỗi lần chúng tôi chọn giá trị nhỏ hơn ở đầu một nửa, chúng ta sẽ di chuyển chỉ mục của mục nào cần so sánh với một mục.

def merge(left_list, right_list):  
    sorted_list = []
    left_list_index = right_list_index = 0

    # We use the list lengths often, so its handy to make variables
    left_list_length, right_list_length = len(left_list), len(right_list)

    for _ in range(left_list_length + right_list_length):
        if left_list_index < left_list_length and right_list_index < right_list_length:
            # We check which value from the start of each list is smaller
            # If the item at the beginning of the left list is smaller, add it
            # to the sorted list
            if left_list[left_list_index] <= right_list[right_list_index]:
                sorted_list.append(left_list[left_list_index])
                left_list_index += 1
            # If the item at the beginning of the right list is smaller, add it
            # to the sorted list
            else:
                sorted_list.append(right_list[right_list_index])
                right_list_index += 1

        # If we've reached the end of the of the left list, add the elements
        # from the right list
        elif left_list_index == left_list_length:
            sorted_list.append(right_list[right_list_index])
            right_list_index += 1
        # If we've reached the end of the of the right list, add the elements
        # from the left list
        elif right_list_index == right_list_length:
            sorted_list.append(left_list[left_list_index])
            left_list_index += 1

    return sorted_list


def merge_sort(nums):  
    # If the list is a single element, return it
    if len(nums) <= 1:
        return nums

    # Use floor division to get midpoint, indices must be integers
    mid = len(nums) // 2

    # Sort and merge each half
    left_list = merge_sort(nums[:mid])
    right_list = merge_sort(nums[mid:])

    # Merge the sorted lists into a new one
    return merge(left_list, right_list)


# Verify it works
random_list_of_nums = [120, 45, 68, 250, 176]  
random_list_of_nums = merge_sort(random_list_of_nums)  
print(random_list_of_nums)  

Lưu ý rằng hàm merge_sort (), không giống như các thuật toán sắp xếp trước đó, trả về một danh sách mới được sắp xếp, thay vì sắp xếp danh sách hiện có. Do đó, merge sort yêu cầu không gian để tạo một danh sách mới có cùng kích thước với danh sách đầu vào.

Độ phức tạp thời gian

Trước tiên chúng ta hãy xem chức năng merge. Phải mất hai danh sách và lặp lại n lần, trong đó n là kích thước của đầu vào kết hợp của chúng. Hàm merge_sort chia mảng đã cho thành 2 và sắp xếp đệ quy các mảng con. Vì đầu vào đang được đệ quy là một nửa của những gì đã được đưa ra, giống như cây nhị phân, điều này làm cho thời gian cần thiết để xử lý tăng logarit theo n.

Do đó, độ phức tạp thời gian tổng thể của thuật toán merge sort là O (nlog (n)).

7. Quick Sort

Thuật toán phân chia và trị này là thuật toán sắp xếp được sử dụng thường xuyên nhất được đề cập trong bài viết này. Khi được định cấu hình chính xác, nó cực kỳ hiệu quả và không yêu cầu sử dụng merge sort. Chúng tôi phân vùng danh sách xung quanh một phần tử trục, sắp xếp các giá trị xung quanh trục

Giải thích

Quick Sort bắt đầu bằng cách phân vùng danh sách - chọn một giá trị của danh sách sẽ ở vị trí được sắp xếp. Giá trị này được gọi là trục. Tất cả các yếu tố nhỏ hơn trục được di chuyển sang bên trái của nó. Tất cả các yếu tố lớn hơn được di chuyển sang bên phải của nó. Biết rằng trục nằm ở vị trí hợp lý, chúng tôi sắp xếp đệ quy các giá trị xung quanh trục cho đến khi toàn bộ danh sách được sắp xếp.

# There are different ways to do a Quick Sort partition, this implements the
# Hoare partition scheme. Tony Hoare also created the Quick Sort algorithm.
def partition(nums, low, high):  
    # We select the middle element to be the pivot. Some implementations select
    # the first element or the last element. Sometimes the median value becomes
    # the pivot, or a random one. There are many more strategies that can be
    # chosen or created.
    pivot = nums[(low + high) // 2]
    i = low - 1
    j = high + 1
    while True:
        i += 1
        while nums[i] < pivot:
            i += 1

        j -= 1
        while nums[j] > pivot:
            j -= 1

        if i >= j:
            return j

        # If an element at i (on the left of the pivot) is larger than the
        # element at j (on right right of the pivot), then swap them
        nums[i], nums[j] = nums[j], nums[i]


def quick_sort(nums):  
    # Create a helper function that will be called recursively
    def _quick_sort(items, low, high):
        if low < high:
            # This is the index after the pivot, where our lists are split
            split_index = partition(items, low, high)
            _quick_sort(items, low, split_index)
            _quick_sort(items, split_index + 1, high)

    _quick_sort(nums, 0, len(nums) - 1)


# Verify it works
random_list_of_nums = [22, 5, 1, 18, 99]  
quick_sort(random_list_of_nums)  
print(random_list_of_nums)  

Độ phức tạp thời gian

Trường hợp xấu nhất là khi phần tử nhỏ nhất hoặc lớn nhất luôn được chọn làm trục. Điều này sẽ tạo các phân vùng có kích thước n-1, gây ra các cuộc gọi đệ quy n-1 lần. Điều này dẫn chúng ta đến độ phức tạp trong trường hợp xấu nhất của O (n ^ 2).

Mặc dù đây là trường hợp xấu nhất , Quick Sort được sử dụng rất nhiều vì độ phức tạp thời gian trung bình nhanh hơn nhiều. Trong khi hàm phân vùng sử dụng các vòng lặp lồng nhau trong khi các vòng lặp, nó sẽ so sánh trên tất cả các phần tử của mảng để thực hiện các giao dịch hoán đổi của nó. Như vậy, nó có độ phức tạp thời gian là O (n).

Với một trục tốt, chức năng Quick Sort sẽ phân vùng mảng thành một nửa, phát triển logarit với n. Do đó, độ phức tạp thời gian trung bình của thuật toán Quick Sort là O (nlog (n))

8 . Các hàm sắp xếp tích hợp của Python

Mặc dù có ích khi hiểu các thuật toán sắp xếp này, trong hầu hết các dự án Python, bạn có thể sẽ sử dụng các hàm sắp xếp đã được cung cấp trong ngôn ngữ. Chúng ta có thể thay đổi danh sách của mình để sắp xếp nội dung bằng phương thức sort ():

apples_eaten_a_day = [2, 1, 1, 3, 1, 2, 2]  
apples_eaten_a_day.sort()  
print(apples_eaten_a_day) # [1, 1, 1, 2, 2, 2, 3]  

Hoặc chúng ta có thể sử dụng hàm sorted () để tạo danh sách được sắp xếp mới:

apples_eaten_a_day_2 = [2, 1, 1, 3, 1, 2, 2]  
sorted_apples = sorted(apples_eaten_a_day_2)  
print(sorted_apples) # [1, 1, 1, 2, 2, 2, 3]  

Cả hai đều sắp xếp theo thứ tự tăng dần, nhưng bạn có thể dễ dàng sắp xếp theo thứ tự giảm dần bằng cách đặt flag đảo ngược thành True:

# Reverse sort the list in-place
apples_eaten_a_day.sort(reverse=True)  
print(apples_eaten_a_day) # [3, 2, 2, 2, 1, 1, 1]

# Reverse sort to get a new list
sorted_apples_desc = sorted(apples_eaten_a_day_2, reverse=True)  
print(sorted_apples_desc) # [3, 2, 2, 2, 1, 1, 1]  

Không giống như các hàm thuật toán sắp xếp mà chúng ta đã tạo, cả hai hàm này có thể sắp xếp danh sách các bộ dữ liệu và các lớp. Hàm sort () có thể sắp xếp bất kỳ đối tượng lặp nào, bao gồm - danh sách, chuỗi, bộ dữ liệu, từ điển, bộ và trình lặp tùy chỉnh mà bạn có thể tạo. Các hàm sắp xếp này thực hiện thuật toán Tim Sort , một thuật toán được lấy cảm hứng từ Merge Sort and Insertion Sort.

9 . So sánh tốc độ

Để có được ý tưởng về việc chúng thực hiện nhanh như thế nào, chúng tôi tạo ra một danh sách 5000 số từ 0 đến 1000. Sau đó chúng tôi sẽ mất bao lâu để mỗi thuật toán hoàn thành. Điều này được lặp lại 10 lần để chúng ta có thể thiết lập một mô hình hiệu suất đáng tin cậy hơn. 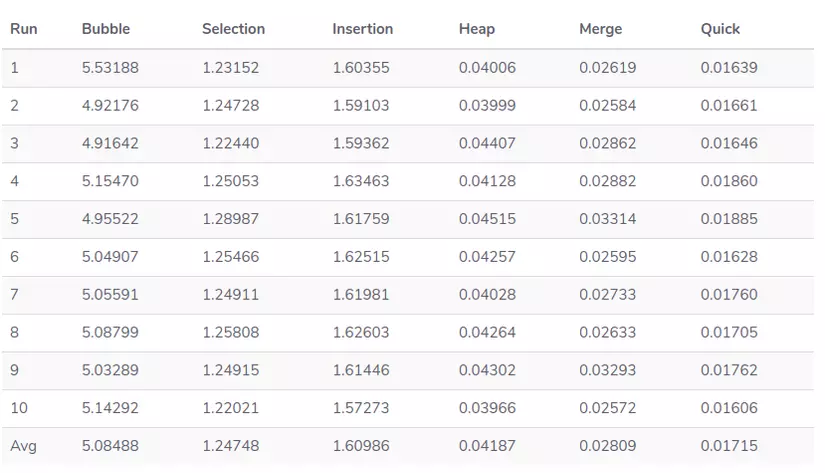Bạn sẽ nhận được các giá trị khác nhau nếu bạn tự thiết lập thử nghiệm, nhưng các mẫu được quan sát phải giống hoặc tương tự nhau. Bubble Sort là trình diễn chậm nhất trong tất cả các thuật toán. Mặc dù nó hữu ích như là một giới thiệu về sắp xếp và thuật toán, nó không phù hợp để sử dụng thực tế.

Chúng tôi cũng nhận thấy rằng Quick Sort rất nhanh, nhanh gần gấp đôi so với merge sort và nó sẽ không cần nhiều không gian để chạy. Hãy nhớ rằng phân vùng của chúng ta dựa trên yếu tố giữa của danh sách, các phân vùng khác nhau có thể có kết quả khác nhau.

Vì Insertion Sort thực hiện so sánh ít hơn nhiều so với Selection Sort, việc triển khai thường nhanh hơn nhưng trong các lần chạy này, Selection Sort nhanh hơn một chút.

Insertion Sort thực hiện nhiều hoán đổi hơn so với Selection Sort. Nếu các giá trị hoán đổi chiếm nhiều thời gian hơn so với so sánh các giá trị, thì kết quả "trái ngược" này sẽ hợp lý. Hãy chú ý đến môi trường khi chọn thuật toán sắp xếp phù hợp nhất dành cho bạn, vì nó sẽ ảnh hưởng đến hiệu suất.

nguồn : https://stackabuse.com/sorting-algorithms-in-python/