Continue with Machine Learning - Try with Multiple Algorithms
Bài đăng này đã không được cập nhật trong 7 năm
In this post, what we are trying to do is finding a way to test several algorithm then choose the best one.
DATA
The data is from https://www.kaggle.com/uciml/breast-cancer-wisconsin-data/data
Purpose
Our machine learning model here is to predict whether the case diagnosis is benign or malignant (B, M). Let's look at the data:
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import time
df = pd.read_csv('data.csv')
df.head()
id diagnosis radius_mean texture_mean perimeter_mean area_mean \
0 842302 M 17.99 10.38 122.80 1001.0
1 842517 M 20.57 17.77 132.90 1326.0
2 84300903 M 19.69 21.25 130.00 1203.0
3 84348301 M 11.42 20.38 77.58 386.1
4 84358402 M 20.29 14.34 135.10 1297.0
smoothness_mean compactness_mean concavity_mean concave points_mean \
0 0.11840 0.27760 0.3001 0.14710
1 0.08474 0.07864 0.0869 0.07017
2 0.10960 0.15990 0.1974 0.12790
3 0.14250 0.28390 0.2414 0.10520
4 0.10030 0.13280 0.1980 0.10430
... texture_worst perimeter_worst area_worst smoothness_worst \
0 ... 17.33 184.60 2019.0 0.1622
1 ... 23.41 158.80 1956.0 0.1238
2 ... 25.53 152.50 1709.0 0.1444
3 ... 26.50 98.87 567.7 0.2098
4 ... 16.67 152.20 1575.0 0.1374
compactness_worst concavity_worst concave points_worst symmetry_worst \
0 0.6656 0.7119 0.2654 0.4601
1 0.1866 0.2416 0.1860 0.2750
2 0.4245 0.4504 0.2430 0.3613
3 0.8663 0.6869 0.2575 0.6638
4 0.2050 0.4000 0.1625 0.2364
fractal_dimension_worst Unnamed: 32
0 0.11890 NaN
1 0.08902 NaN
2 0.08758 NaN
3 0.17300 NaN
4 0.07678 NaN
[5 rows x 33 columns]
Data Description
There are 10 features measured in 3 ways: mean, standard error, worst. Those 10 features are: Ten real-valued features are computed for each cell nucleus:
a) radius (mean of distances from center to points on the perimeter)
b) texture (standard deviation of gray-scale values)
c) perimeter
d) area
e) smoothness (local variation in radius lengths)
f) compactness (perimeter^2 / area - 1.0)
g) concavity (severity of concave portions of the contour)
h) concave points (number of concave portions of the contour)
i) symmetry
j) fractal dimension ("coastline approximation" - 1)
and diagnosis as malignant or benign (M,B)
Data Exploration
Let's separate the data into features and class label (what we want to predict)
y = df['diagnosis']
x = df.drop(['id', 'diagnosis', 'Unnamed: 32'], axis=1)
x.head()
#Output
radius_mean texture_mean perimeter_mean area_mean smoothness_mean \
0 17.99 10.38 122.80 1001.0 0.11840
1 20.57 17.77 132.90 1326.0 0.08474
2 19.69 21.25 130.00 1203.0 0.10960
3 11.42 20.38 77.58 386.1 0.14250
4 20.29 14.34 135.10 1297.0 0.10030
compactness_mean concavity_mean concave points_mean symmetry_mean \
0 0.27760 0.3001 0.14710 0.2419
1 0.07864 0.0869 0.07017 0.1812
2 0.15990 0.1974 0.12790 0.2069
3 0.28390 0.2414 0.10520 0.2597
4 0.13280 0.1980 0.10430 0.1809
fractal_dimension_mean ... radius_worst \
0 0.07871 ... 25.38
1 0.05667 ... 24.99
2 0.05999 ... 23.57
3 0.09744 ... 14.91
4 0.05883 ... 22.54
texture_worst perimeter_worst area_worst smoothness_worst \
0 17.33 184.60 2019.0 0.1622
1 23.41 158.80 1956.0 0.1238
2 25.53 152.50 1709.0 0.1444
3 26.50 98.87 567.7 0.2098
4 16.67 152.20 1575.0 0.1374
compactness_worst concavity_worst concave points_worst symmetry_worst \
0 0.6656 0.7119 0.2654 0.4601
1 0.1866 0.2416 0.1860 0.2750
2 0.4245 0.4504 0.2430 0.3613
3 0.8663 0.6869 0.2575 0.6638
4 0.2050 0.4000 0.1625 0.2364
fractal_dimension_worst
0 0.11890
1 0.08902
2 0.08758
3 0.17300
4 0.07678
[5 rows x 30 columns]
Let check our data distribution by checking density plot on each feature:
x.plot(kind='density', subplots=True, layout=(6,6), sharex=False, legend=False, fontsize=1)
plt.show()
 All the features quite follow a general gaussian distribution.
Let's check the number of case of benign and malignant
All the features quite follow a general gaussian distribution.
Let's check the number of case of benign and malignant
ax = sns.countplot(y, label="Count")
b, m = y.value_counts()
print("Number of Benign: ", b)
print("Number of Malign: ", m)
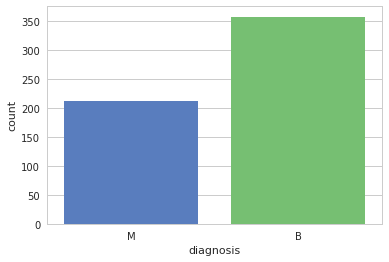
Let's check data statistics:
x.describe()
x.describe()
radius_mean texture_mean perimeter_mean area_mean \
count 569.000000 569.000000 569.000000 569.000000
mean 14.127292 19.289649 91.969033 654.889104
std 3.524049 4.301036 24.298981 351.914129
min 6.981000 9.710000 43.790000 143.500000
25% 11.700000 16.170000 75.170000 420.300000
50% 13.370000 18.840000 86.240000 551.100000
75% 15.780000 21.800000 104.100000 782.700000
max 28.110000 39.280000 188.500000 2501.000000
smoothness_mean compactness_mean concavity_mean concave points_mean \
count 569.000000 569.000000 569.000000 569.000000
mean 0.096360 0.104341 0.088799 0.048919
std 0.014064 0.052813 0.079720 0.038803
min 0.052630 0.019380 0.000000 0.000000
25% 0.086370 0.064920 0.029560 0.020310
50% 0.095870 0.092630 0.061540 0.033500
75% 0.105300 0.130400 0.130700 0.074000
max 0.163400 0.345400 0.426800 0.201200
symmetry_mean fractal_dimension_mean ... \
count 569.000000 569.000000 ...
mean 0.181162 0.062798 ...
std 0.027414 0.007060 ...
min 0.106000 0.049960 ...
25% 0.161900 0.057700 ...
50% 0.179200 0.061540 ...
75% 0.195700 0.066120 ...
max 0.304000 0.097440 ...
radius_worst texture_worst perimeter_worst area_worst \
count 569.000000 569.000000 569.000000 569.000000
mean 16.269190 25.677223 107.261213 880.583128
std 4.833242 6.146258 33.602542 569.356993
min 7.930000 12.020000 50.410000 185.200000
25% 13.010000 21.080000 84.110000 515.300000
50% 14.970000 25.410000 97.660000 686.500000
75% 18.790000 29.720000 125.400000 1084.000000
max 36.040000 49.540000 251.200000 4254.000000
smoothness_worst compactness_worst concavity_worst \
count 569.000000 569.000000 569.000000
mean 0.132369 0.254265 0.272188
std 0.022832 0.157336 0.208624
min 0.071170 0.027290 0.000000
25% 0.116600 0.147200 0.114500
50% 0.131300 0.211900 0.226700
75% 0.146000 0.339100 0.382900
max 0.222600 1.058000 1.252000
concave points_worst symmetry_worst fractal_dimension_worst
count 569.000000 569.000000 569.000000
mean 0.114606 0.290076 0.083946
std 0.065732 0.061867 0.018061
min 0.000000 0.156500 0.055040
25% 0.064930 0.250400 0.071460
50% 0.099930 0.282200 0.080040
75% 0.161400 0.317900 0.092080
max 0.291000 0.663800 0.207500
[8 rows x 30 columns]
Let's check data features corrolletion:
f, ax = plt.subplots(figsize=(18,18))
sns.heatmap(x.corr(), annot=True, linewidths=0.5, fmt='.1f', ax=ax)
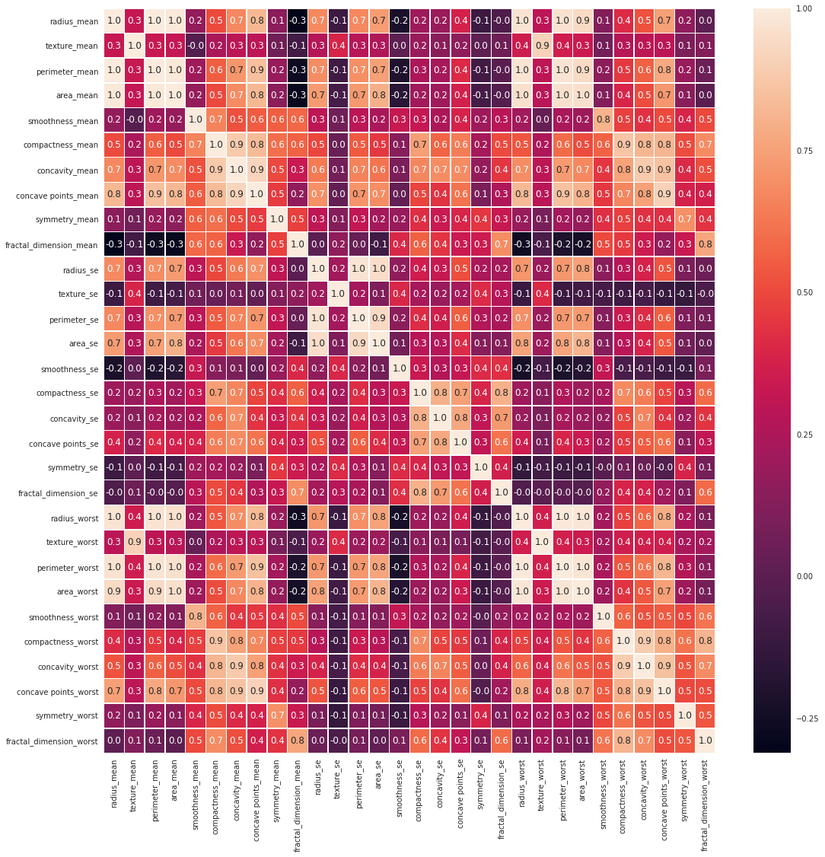
Training model
There are several algorithm that are good for binary classification. We will test with 5 algorithm and check out which one is the best one: Classification and Regression Trees (CART), Linear Support Vector Machines (SVM), Gaussian Naive Bayes (NB) and k-Nearest Neighbors (KNN) and RandomForestClassifier(RF).
from sklearn.model_selection import KFold, cross_val_score
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC, LinearSVC
models = []
models.append(('CART', DecisionTreeClassifier()))
models.append(('SVM', SVC()))
models.append(('NB', GaussianNB()))
models.append(('KNN', KNeighborsClassifier()))
models.append(('LinearSVC', LinearSVC()))
num_folds = 10
results = []
names = []
kfold = KFold(n_splits=num_folds, random_state=123)
for name, model in models:
start = time.time()
cv_results = cross_val_score(model, x_train, y_train, cv=kfold, scoring='accuracy')
end = time.time()
results.append(cv_results)
names.append(name)
print("%s: %f (%f) (run time: %f)" % (name, cv_results.mean(), cv_results.std(), end-start))
#Output
CART: 0.919551 (0.024681) (run time: 0.069104)
SVM: 0.625769 (0.074918) (run time: 0.569782)
NB: 0.921987 (0.034719) (run time: 0.039054)
KNN: 0.901859 (0.044437) (run time: 0.046674)
RF: 0.934679 (0.032022) (run time: 0.326259)
Let's make a graph of the performance
fig = plt.figure()
fig.suptitle('Performance Comparision')
ax= fig.add_subplot(111)
plt.boxplot(results)
ax.set_xticklabels(names)
plt.show()
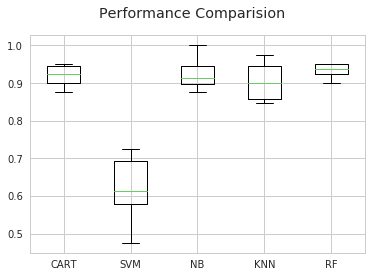
We find that the svm performance is not so good. This may be due to data not scaled yet. Let's scale before training check the performance again.
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
import warnings
pipelines = []
pipelines.append(('ScaledCART', Pipeline([('Scaler', StandardScaler()), ('CART', DecisionTreeClassifier())])))
pipelines.append(('ScaledSVM', Pipeline([('Scaler', StandardScaler()), ('SVM', SVC())])))
pipelines.append(('ScaledNB', Pipeline([('Scaler', StandardScaler()), ('NB', GaussianNB())])))
pipelines.append(('ScaledKNN', Pipeline([('Scaler', StandardScaler()), ('KNN', KNeighborsClassifier())])))
pipelines.append(('ScaledRF', Pipeline([('Scaler', StandardScaler()), ('RF', RandomForestClassifier())])))
results = []
names = []
with warnings.catch_warnings():
warnings.simplefilter('ignore')
kfold = KFold(n_splits=num_folds, random_state=123)
for name, model in pipelines:
start = time.time()
cv_results = cross_val_score(model, x_train, y_train, cv=kfold, scoring='accuracy')
end = time.time()
results.append(cv_results)
names.append(name)
print("%s: %f (%f) (%f)" % (name, cv_results.mean(), cv_results.std(), end-start))
#Output
ScaledCART: 0.937179 (0.025657) (0.154313)
ScaledSVM: 0.969744 (0.027240) (0.134548)
ScaledNB: 0.937051 (0.039612) (0.058743)
ScaledKNN: 0.952115 (0.043058) (0.091208)
ScaledRF: 0.949744 (0.031627) (0.405433)

There are a lot of improvement. and SVM is the best.
Here is the crux of this post. We will use GridSearchCV from model_selection to run each important params to tune for the best params.
from sklearn.model_selection import GridSearchCV
scaler = StandardScaler().fit(x_train)
scaledX = scaler.transform(x_train)
c_values = [round(0.1 * (i+1), 1) for i in range(20)]
kernel_values = ['linear', 'poly', 'rbf', 'sigmoid']
params_grid = dict(C=c_values, kernel=kernel_values)
kfold = KFold(n_splits=num_folds, random_state=121)
grid = GridSearchCV(estimator=SVC(), param_grid=params_grid, scoring='accuracy', cv=kfold)
grid_result = grid.fit(scaledX, y_train)
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
means = grid_result.cv_results_['mean_test_score']
stds = grid_result.cv_results_['std_test_score']
params = grid_result.cv_results_['params']
for mean, std, param in zip(means, stds, params):
print("%f (%f) with: %r" % (mean, std, param))
#Output
Best: 0.972362 using {'C': 0.1, 'kernel': 'linear'}
0.972362 (0.026491) with: {'C': 0.1, 'kernel': 'linear'}
0.841709 (0.053980) with: {'C': 0.1, 'kernel': 'poly'}
0.932161 (0.039436) with: {'C': 0.1, 'kernel': 'rbf'}
0.939698 (0.020594) with: {'C': 0.1, 'kernel': 'sigmoid'}
0.964824 (0.036358) with: {'C': 0.2, 'kernel': 'linear'}
0.861809 (0.040516) with: {'C': 0.2, 'kernel': 'poly'}
0.947236 (0.030812) with: {'C': 0.2, 'kernel': 'rbf'}
0.944724 (0.022233) with: {'C': 0.2, 'kernel': 'sigmoid'}
0.962312 (0.034665) with: {'C': 0.3, 'kernel': 'linear'}
0.866834 (0.043296) with: {'C': 0.3, 'kernel': 'poly'}
0.952261 (0.028829) with: {'C': 0.3, 'kernel': 'rbf'}
0.954774 (0.027544) with: {'C': 0.3, 'kernel': 'sigmoid'}
0.959799 (0.038022) with: {'C': 0.4, 'kernel': 'linear'}
0.869347 (0.042970) with: {'C': 0.4, 'kernel': 'poly'}
0.957286 (0.030066) with: {'C': 0.4, 'kernel': 'rbf'}
0.959799 (0.025934) with: {'C': 0.4, 'kernel': 'sigmoid'}
0.959799 (0.038022) with: {'C': 0.5, 'kernel': 'linear'}
0.871859 (0.046718) with: {'C': 0.5, 'kernel': 'poly'}
0.967337 (0.027764) with: {'C': 0.5, 'kernel': 'rbf'}
0.954774 (0.027398) with: {'C': 0.5, 'kernel': 'sigmoid'}
0.959799 (0.034560) with: {'C': 0.6, 'kernel': 'linear'}
0.876884 (0.042568) with: {'C': 0.6, 'kernel': 'poly'}
0.967337 (0.027764) with: {'C': 0.6, 'kernel': 'rbf'}
0.959799 (0.030474) with: {'C': 0.6, 'kernel': 'sigmoid'}
0.959799 (0.034560) with: {'C': 0.7, 'kernel': 'linear'}
0.884422 (0.046459) with: {'C': 0.7, 'kernel': 'poly'}
0.967337 (0.027764) with: {'C': 0.7, 'kernel': 'rbf'}
0.962312 (0.028466) with: {'C': 0.7, 'kernel': 'sigmoid'}
0.957286 (0.034271) with: {'C': 0.8, 'kernel': 'linear'}
0.894472 (0.043221) with: {'C': 0.8, 'kernel': 'poly'}
0.972362 (0.026400) with: {'C': 0.8, 'kernel': 'rbf'}
0.959799 (0.028338) with: {'C': 0.8, 'kernel': 'sigmoid'}
0.957286 (0.034271) with: {'C': 0.9, 'kernel': 'linear'}
0.896985 (0.041029) with: {'C': 0.9, 'kernel': 'poly'}
0.969849 (0.027207) with: {'C': 0.9, 'kernel': 'rbf'}
0.959799 (0.028338) with: {'C': 0.9, 'kernel': 'sigmoid'}
0.959799 (0.034560) with: {'C': 1.0, 'kernel': 'linear'}
0.902010 (0.039532) with: {'C': 1.0, 'kernel': 'poly'}
0.969849 (0.027207) with: {'C': 1.0, 'kernel': 'rbf'}
0.947236 (0.026665) with: {'C': 1.0, 'kernel': 'sigmoid'}
0.957286 (0.034271) with: {'C': 1.1, 'kernel': 'linear'}
0.902010 (0.039532) with: {'C': 1.1, 'kernel': 'poly'}
0.969849 (0.027207) with: {'C': 1.1, 'kernel': 'rbf'}
0.962312 (0.030593) with: {'C': 1.1, 'kernel': 'sigmoid'}
0.957286 (0.034271) with: {'C': 1.2, 'kernel': 'linear'}
0.902010 (0.039532) with: {'C': 1.2, 'kernel': 'poly'}
0.969849 (0.027207) with: {'C': 1.2, 'kernel': 'rbf'}
0.954774 (0.037240) with: {'C': 1.2, 'kernel': 'sigmoid'}
0.959799 (0.034560) with: {'C': 1.3, 'kernel': 'linear'}
0.902010 (0.039532) with: {'C': 1.3, 'kernel': 'poly'}
0.969849 (0.027207) with: {'C': 1.3, 'kernel': 'rbf'}
0.947236 (0.030890) with: {'C': 1.3, 'kernel': 'sigmoid'}
0.957286 (0.032387) with: {'C': 1.4, 'kernel': 'linear'}
0.902010 (0.039532) with: {'C': 1.4, 'kernel': 'poly'}
0.969849 (0.027207) with: {'C': 1.4, 'kernel': 'rbf'}
0.947236 (0.030812) with: {'C': 1.4, 'kernel': 'sigmoid'}
0.962312 (0.034665) with: {'C': 1.5, 'kernel': 'linear'}
0.907035 (0.042054) with: {'C': 1.5, 'kernel': 'poly'}
0.969849 (0.027207) with: {'C': 1.5, 'kernel': 'rbf'}
0.939698 (0.030308) with: {'C': 1.5, 'kernel': 'sigmoid'}
0.962312 (0.034665) with: {'C': 1.6, 'kernel': 'linear'}
0.907035 (0.042054) with: {'C': 1.6, 'kernel': 'poly'}
0.967337 (0.025401) with: {'C': 1.6, 'kernel': 'rbf'}
0.942211 (0.030020) with: {'C': 1.6, 'kernel': 'sigmoid'}
0.962312 (0.034665) with: {'C': 1.7, 'kernel': 'linear'}
0.907035 (0.042054) with: {'C': 1.7, 'kernel': 'poly'}
0.967337 (0.025401) with: {'C': 1.7, 'kernel': 'rbf'}
0.934673 (0.037762) with: {'C': 1.7, 'kernel': 'sigmoid'}
0.962312 (0.034665) with: {'C': 1.8, 'kernel': 'linear'}
0.907035 (0.042054) with: {'C': 1.8, 'kernel': 'poly'}
0.967337 (0.025401) with: {'C': 1.8, 'kernel': 'rbf'}
0.934673 (0.039574) with: {'C': 1.8, 'kernel': 'sigmoid'}
0.962312 (0.034665) with: {'C': 1.9, 'kernel': 'linear'}
0.907035 (0.042054) with: {'C': 1.9, 'kernel': 'poly'}
0.969849 (0.027207) with: {'C': 1.9, 'kernel': 'rbf'}
0.937186 (0.041050) with: {'C': 1.9, 'kernel': 'sigmoid'}
0.962312 (0.034665) with: {'C': 2.0, 'kernel': 'linear'}
0.909548 (0.037588) with: {'C': 2.0, 'kernel': 'poly'}
0.969849 (0.027207) with: {'C': 2.0, 'kernel': 'rbf'}
0.937186 (0.042723) with: {'C': 2.0, 'kernel': 'sigmoid'}
We found the best params. Now let's apply and test our test data.
scaler = StandardScaler().fit(x_train)
scaledx = scaler.transform(x_train)
model = SVC(C=0.1, kernel='linear')
start = time.time()
model.fit(scaledx, y_train)
end = time.time()
print("Run time: %f" % (end-start))
scaledx = scaler.transform(x_test)
y_predicted = model.predict(scaledx)
print("Accuracy score: %f" % accuracy_score(y_test, y_predicted))
print(classification_report(y_test, y_predicted))
print(confusion_matrix(y_test, y_predicted))
#Output
Run time: 0.003853
Accuracy score: 0.988304
precision recall f1-score support
B 0.99 0.99 0.99 103
M 0.99 0.99 0.99 68
avg / total 0.99 0.99 0.99 171
[[102 1]
[ 1 67]]
Reference
All rights reserved