Cây quyết định - Decision Tree

Bài viết được dịch từ

Cây quyết định là một trong những thuật toán máy học phổ biến nhất hiện nay. Nó được dùng trong cả bài toán phân lớp và hồi quy. Trong bài viết này, mình sẽ giải quyết bài toán phân lớp.

Trước khi bắt đầu, mình có một câu hỏi :v

Vì sao lại là câu quyết định

Chúng ta có một vài thuật toán nhưng vì sao chúng ta phải chọn cây quyết định?

Có một vài câu trả lời nhưng mình nghĩ đến 2 câu trả lời dưới đây:

1. Cây quyết định bắt trước mức độ suy nghĩ của con người nên nó đơn giản để hiểu và chuẩn bị dữ liệu.
2. Cây quyết định giúp bạn thấy được logic từ dữ liệu

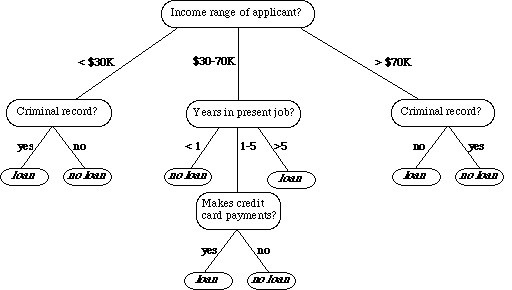
Ví dụ: nếu chúng ta đang phân lớp ứng dụng vay ngân hàng cho khác hàng, cây quyết định sẽ nhìn giống như trong ảnh.

Chúng ta có thể nhìn thấy được sự logic về việc xây dựng cây quyết định. Khá đơn giản và rõ ràng.

Vậy cây quyết định là gì?

Cây quyết định là cây mà mỗi nút biểu diễn một đặc trưng(tính chất), mỗi nhánh(branch) biểu diễn một quy luật(rule) và mỗi lá biểu biễn một kết quả (giá trị cụ thể hay một nhánh tiếp tục)

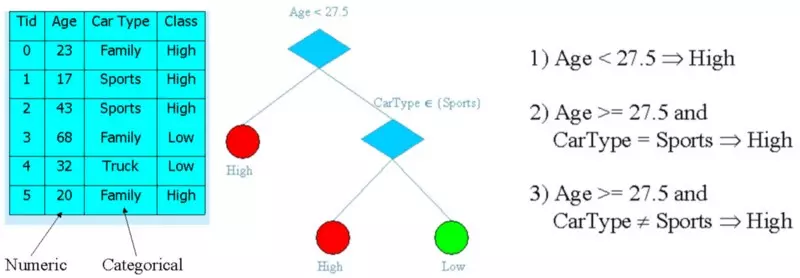
Xây dựng một cây quyết định như thế nào?

Có một vài thuật toán để tạo một cây quyết định, chúng ta sẽ nói về 2 trong số chúng:

1. CART (Classification and Regression Trees) → dùng Gini Index(Classification) để kiểm tra.
2. ID3 (Iterative Dichotomiser 3) → dùng Entropy function và Information gain để kiểm tra.

Cùng tạo cây quyết định để giải quyết bài toán phân lớp bằng những thuật toán trên ^^

Phân lớp bằng thuật toán ID3

Mình sẽ dùng tập dữ liệu nổi tiếng trong ngành máy học - dữ liệu thời tiết(weather dataset) - đưa ra yes or no dựa vào thời tiết.

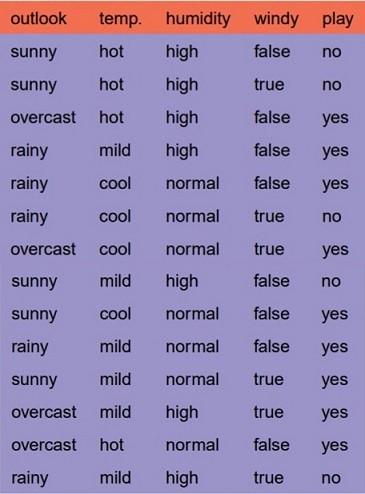
Chúng ta có 4 X giá trị (quang cảnh - outlook, nhiệt độ-temp, độ ẩm-humidity, gió-windy) và một giá trị Y( đi chơi hay k? - yes or no ) đã được chỉ rõ.

Chúng ta cần tìm sự ánh xạ giữa X và Y ( mỗi liên hệ giữa input và output)

Đây là bài toán phân lớp nhị phân nên hãy dùng ID3

Để xây dựng cây, trước hết chúng ta cần nút gốc và ta biết root là một trong những đặc trưng(tính chất).

Vậy, chúng ta chọn gốc(root) như thề nào? Chúng ta chọn đặc trưng có imformation gain(IG) cao nhất trong ID3

Để xác định IG chính xác, chúng ta định nghĩa một thước đo thường được dùng trong lí thuyết thông tin, gọi là entropy miêu tả độ trong sạch của một thu thập dữ liệu tùy ý.

Với bài toán phân lớp:

• Nếu ví dụ là dương và tất cả là âm thì entropy = 0.
• Nếu một nửa của ví dụ là dương và một nửa âm thì entropy =1.

Giờ hãy ứng dụng IG để tìm gốc:

1. Tính toán entropy cho tập dữ liệu.
2. Với tất cả đặc trưng:
    1. Tính toán entropy của tất cả giá trị.
    2. Tính entropy trung bình cho thuộc tính đang thực hiện.
3. Chọn đặc trưng chó IG cao nhất.
4. Lặp lại cho đến khi thu được cây như mong muốn.

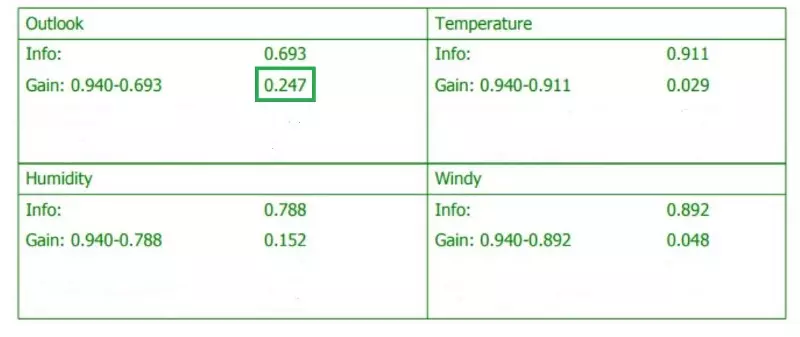
Tính entropy của dữ liệu: Tính toán IG và entropy cho tất cả đặc trưng Tương tự chúng ta có thể tính IG và entropy cho 2 đặc trưng còn lại. Chọn giá trị có gain cao nhất

Suy ra, nút gốc của ta là Outlook.!

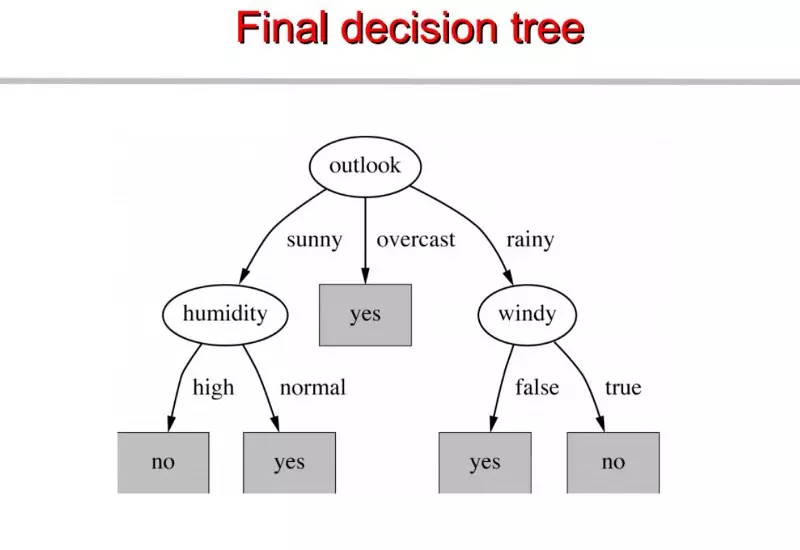
Lặp lại đén khi nhận được kết quả cuối cùng. Cuối cùng ta có được kết quả:

Trên đây là cách mà cây quyết định giải quyết bài toán phân lớp bằng bài thuật toán ID3. Cảm ơn mọi người vì đã đọc bài việt ...