Đã đăng vào thg 8 23, 2018 5:27 CH 8 phút đọc

6.8K

CẤU TRÚC DỮ LIỆU VÀ GIẢI THUẬT

Bài đăng này đã không được cập nhật trong 5 năm

CHƯƠNG 2. THIẾT KẾ VÀ PHÂN TÍCH GIẢI THUẬT

2.2. Thiết kế giải thuật

2.1.1. Phân rã bài toán thành các bài toán nhỏ hơn.

Các bài toán giải trên máy tính càng ngày càng đa dạng và phong phú dẫn tới quy mô chương trình ngày càng lớn. Quy mô càng lớn dẫn tới việc lập và kiểm soát chương tình càng gặp nhiều khó khăn hơn.
Ta cần chia bài toán lớn thành nhiều bài toán nhỏ, do đó người ta sử dụng một phương pháp thiết kế:

Từ trên xuống (top)-down design : phân tích tổng quát toàn bộ vấn đề và mục tiêu đặt ra, đè cập tới những công việc chủ yếu, sau đó dần giải quyết các phần việc cụ thể một cách chi tiết hơn.

Ví dụ: Cần lập một hệ chương trình quản lý bảo trì hồ sơ về lương của cán bộ, công nhận một xí nghiệp, hàng tháng phải in ra bảng lương của xí nghiệp.

Chương trình được phân tích theo sơ đồ sau:
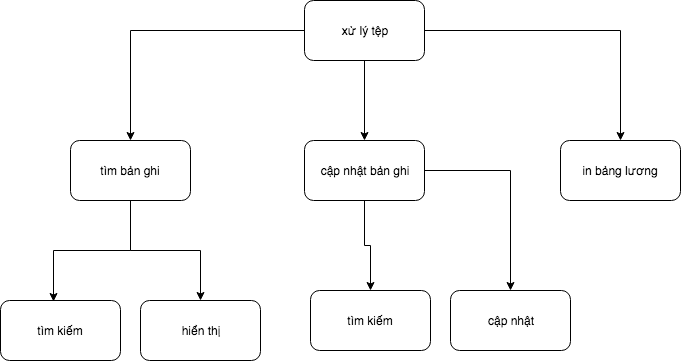
Ưu điểm cho phương pháp thiết kế từ trên xuống:
- Giúp cho việc giải quyết bài toán được định hướng rõ ràng, tránh sa đà vào các chi tiết phụ.
- Cho phép tách bài toán thành các thành phần độc lập, mỗi phần có thể được giao cho các nhóm lập trình khác nhau. Các nhóm làm việc độc lập với nhau.
- Thấy cấu trúc rõ ràng của chương trình, từ đó có thể dễ dàng hiểu, nắm vững và bao quát chương trình, việc tìm và sửa lỗi cũng trở nên dễ dàng hơn.

2.1.2. Phương pháp tính chỉnh từng bước.

Phương pháp tinh chỉnh từng bước là phương pháp thiết kế giải thật gắn liền với lập trình.

Ví dụ: Lập chương trình sắp xếp một dãy số gồm n số nguyên theo thứ tự tăng dần.

Các bước tinh chỉnh sẽ như sau:

1. Readln(n)
2. Lần lượt nhập các số a1, a2, ..., an
3. For i:=1 to n do
    Begin
    - Tìm số nhỏ nhất a_min trong dãy ai, ai+1, ... , an
    - đổi chỗ a_min với ai
    End

Tới đây ta thấy trong phần 3 chỉ có 2 nhiệm vụ cần làm rõ:
- Tìm số nhỏ nhất $a_min$
- đổi chỗ $a_min$ với $a_i$
Số nhỏ nhất được xác định bằng cách chỉ ra vị trí của nó, tức là xác định chỉ số của nó. Việc này được thực hiện bằng cáh luôn ghi nhớ chỉ số của Số nhỏ nhất vào 1 biến, cụ thể là:

    min:=i;
    For k:=i+1 to n do
    If ai < amin then min:=k;

Việc đổi chỗ $a_min$ với $a_i$ được thực hiện giống nhau như khi ta muốn chuyển 2 thứ nước trong 2 chai từ chai nọ sang chai kia, ta dùng 1 chai thứ 3 làm trung gian.

    tg:=ai;
    a:=amin;
    amin:=tg;

Sau khi tinh chỉnh lần 2, chương trình có dạng:

    1. Readln(n)
    2. Lần lượt nhập các số a1, a2, ..., an
    3. For i:=1 to n do
    Begin
        3.1.  min:=i;
            For k:=i+1 to n do 
            If a[k] < a[min] then min:=k;
        3.2. tg:=a[i];
             a[i]:=a[min];
             a[min]:=tg;
    End

2.2. Phân tích giải thuật.

Trong quá tình xây dựng thuật toán và chương trình để giải bài toán có 1 số yêu cầu về phân tích, đánh giá được đặt ra. Trước hết cần phân tích, đánh giá tính đúng đắn của thuật toán, tiếp đó đến tính đơn giản và hiệu quả.

2.2.1. Phân tính tính đúng đắn của giải thuật.

2.2.2. Phân tích tính đơn giản của giải thuật.

trong trường hợp các chương trình chỉ được sử dụng vài lần thì sự lựa chọn của chúng ta là tính đơn giản, vi thời gian thưc hiện và công sức xây dựng chương trình lớn hơn rất nhiều so với thời gian thực hiện chương trình.
Trong trường hợp chương trình được sử dụng nhiều lần, nhất là với các ứng dụng mà thời gian thực hiện đòi hỏi rất nhanh hoặc khối lượng dữ liệu vào lớn thì ưu tiên của chúng tal lại là các giải thuật hiệu quả, thời gian thực hiện ngắn, tiết kiệm bộ nhớ.

2.2.3. Phân tích thời gian thực hiện giải thuật.

a) Đặt vấn đề.

Nếu gọi n là số lượng dữ liệu vào thì có thể xem thời gian thực hiện của 1 giải thuật là hàm số n: $T(n)$
Ở đây ta chỉ xét các trường hợp n khá lớn (với n nhỏ thì việc xét $T(n)$ không có ý nghĩa). Giả sử để giải quyết 1 bài toán cho trước ta có 2 giải thuật:
- Giải thuật $T_1$ với thời gian thực hiện là $T_1(n)=cn^2$ (c là hằng số).
- Giải thuật $T_2$ với thời gian thực hiện là $T_2(n)$ =kn (k là hằng số).

Cách đánh giá thời gian thực hiện giải thuật đọc lập với máy tính và yếu tố liên quan tới máy tính như trên dẫn ta tới khái niệm "cấp độ lớn của thời gian thực hiện giải thuật", còn gọi là "độ phức tạp cảu giải thuật".

b) Độ phức tạp tính toán của giải thuật.

Thông thường các hàm thể hiện độ phức tạp tính toán của giải thuật có dạng $log_2n, n, nlog_2n, n^2, n^3, 2^n, n!, n^n$ .
Các hàm $log_2n, n, nlog_2n, n^2, n^3$ gọi là các hàm loại đa thức.
Các hàm $2^n, n!, n^n$ được gọi là các hàm loại mũ.
Nếu giải thuật có thời gian thực hiện có cấp hàm đa thức thì thời gian thực hiện tương đối ngắn, thường là có thể chấp nhận được, còn nếu thời gian thực hiện có cấp hàm mũ thì tốc độ quá châm, cần phải tìm cách làm khác.

c) Xác định độ phức tạp tính toán của giải thuật.

Quy tắc tổng

Ví dụ: Giả sử chương trình có 3 bước thực hiện mà thời gian thực hiện lần lượt là $O(n), O(nLog_2n) và O(n^3)$ khi đó thời gian thực hiện 2 bước đầu là $O(MAX(n, nlog_2n)) = O(nlog_2n)$ thì thời gian thực hiển chương trình là:
$O(MAX(n^3, nlog_2n)) = O(n^3)$

Nhận xét: qua chứnng mình trên có thể thấy : nếu $g(n) \leqslant f(n) \forall n$ thoả mãn $n \geqslant n_0$ thì $O(f(n) + g(n)) = O(n^3)$

Quy tắc nhân

Ví dụ: câu lệnh $x := x+1$ có thời gian thực hiện là c, được đáh giá là O(1).
Câu lệnh:
For i:=1 To n do x:=x+1;
Có thời gian thực hiện là O(n).
Câu lệnh
For i:=1 To n do For j:=i To n do x:=x+1;
Có thời gian thực hiện là O(n^2).

Từ các nhận xét trên khi đánh gía thời gina thực hiện giải thuật ta chỉ cần chú ý tới các bước tương ứng của phép toán được thực hiện nhiều lần nhất. (Phép toán đó gọi là phép toán tích cực).

Ví dụ để tính giá trị của $e^x$ theo công thức:
$e^x = 1 + \frac {x} {1!} + \frac {x^2} {2!} + ... + \frac {x^n} {n!}$ với x và n cho trước, ta có thể sử dụng giải thuật sau:

    1. Read(x);
       S := 1;
    2. For i:= 1 to n do
       Begin 
           p := 1;
           For j:=1 to i do p:=p*x/j;
           S := S + p;
       End

Ở đây phép p := p*x/j được thực hiện nhiều lần nhất, là phép toán tích cực. Số lần thực hiện phép toán này là $\frac {n(n + 1)} {2}$
Thời gian thực hiện thuật toán được đánh giá là $T(n) = O(n^2)$
Ví dụ: cũng bài toán trên ta có thể dùng giải thuật sau với độ phức tạp nhỏ hơn:

    1. Read(x);
      S := 1;
      P := 1;
   2. For i:= 1 to n do
      Begin 
          p := p*x/i;
          S := S + p;
      End

Số lần thực hiện phép p := p*x/i là n, do đó $T(n) = O(n)$