Cấu trúc dữ liệu tuyến tính trong Javascript: Linked Lists, Stacks và Queues

Bài viết này mình sẽ cùng với các bạn tìm hiểu một số dạng cấu trúc dữ liệu (data structure) có thể sử dụng trong Javascript. Chắc hẳn các bạn đã rất quen thuộc với mảng (array) hay các đối tượng (object) chứa các cặp key-value rồi, thế còn linked list, stack, queue thì sao nhỉ?

Linked list

Tạm dịch: danh sách liên kết

Linked list giống như một chuỗi các hộp được liên kết liền kề với nhau và được đặt trong một căn phòng tối vậy. Tại sao lại là "phòng tối" vì bạn không thể xác định được ngay lập tức vị trí của một hộp bất kì. Để đi đến một hộp nào đó, yêu cầu bạn phải bắt đầu từ điểm đầu mút (head/ đầu hoặc tail/ đuôi) của chuỗi hộp đó sau đó duyệt lần lượt từng hộp, rồi sang hộp kế tiếp. Khi bạn sang đến một hộp nào đó, nó sẽ điều hướng bạn tiến về phía trước sang hộp nối tiếp. Khác với dạng cấu trúc dữ liệu mảng, không tồn tại giá trị index của từng phần tử trong danh sách, mà bạn có thể dùng nó để nhảy trực tiếp đến phần tử đó.

Với Linked list, bạn có thể dễ dàng:

• unshift: thêm một hộp vào đầu chuỗi và set nó thành head mới của chuỗi.
• push: thêm một hộp vào cuối chuỗi và sett nó thành tail mới của chuỗi.
• shift: bỏ hộp đầu tiên của chuỗi.
• pop: bỏ hộp cuối cùng của chuỗi.

vì head và tail của chuỗi là 2 phần tữ dễ dàng tiếp cận nhất.

Nhưng nếu bạn muốn insert hay remove một hộp mới hay bỏ thêm item vào một hộp nằm đâu đó giữa head và tail thì chuyện trở nên "khó nhằn" hơn một chút. Cách làm đòi hỏi bạn phải bắt đầu từ điểm đầu mút, rồi duyệt qua từng phần tử của chuỗi cho đến khi bạn đến được vị trí mong muốn.

Có 2 loại Linked list:

Singly linked list

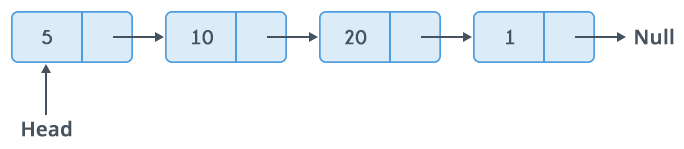
Là linked list một chiều, có nghĩa bạn chỉ có thể duyệt tịnh tiến theo một chiều từ head cho đến tail của chuỗi. Độ phức tạp của phép unshift, shift, hay push là O(1) vì bạn chỉ cần duyệt phần tử đầu tiên của chuỗi là head hoặc tail Nhưng để pop, sau khi bạn bỏ phần tử cuối cùng của chuỗi đi, bạn phải gán lại tail cho phần tử kế phần tử vừa bị bỏ đi. điều này chỉ có thể thực hiện khi bạn duyệt từ head và duyệt dần cho đến phần tử đó. Do đó độ phức tạp sẽ là O(n). Số hộp là n thì sẽ cần n bước để duyệt đến phần tử cuối, và assign tail cho nó.

Tương tự, việc insert/remove hộp hay get/set item vào bất kì hộp nào giữa head và tail cũng cần bạn phải duyệt bắt đầu từ head và vì thế độ phức tạp sẽ cùng là O(n)

Doubly linked list

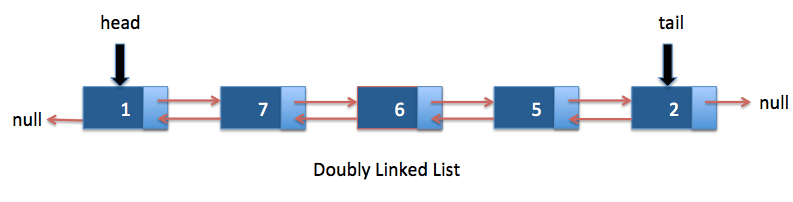
là linked list 2 chiều, đồng nghĩa bạn có thể duyệt tịnh tiến từ cả head hoặc tail. Độ phức tập của tất cả các phép unshift, shift, push hay pop đều là O(1), sau khi bạn pop tail, bạn có thể gán tail ngay cho phần tử cuối cùng hiện tại.

Một lợi ích khác khi bạn có thể duyệt từ cả 2 đầu cuối của chuỗi, đó là khi thực thi các phép insert/remove hộp hoặc get/set items vào hộp giữa tail và head thời gian cần chỉ bằng một nửa so với singly linked list, vì độ phức tạp của nó đã giảm một nửa. Lý do là vì, giả sử hộp bạn tìm nằm ở nửa giữa thứ 2 của chuỗi, bằng việc duyệt từ tail của chuỗi, bạn không phải duyệt qua nửa đầu của chuỗi.

Stack

Tạm dịch: bộ xếp chồng

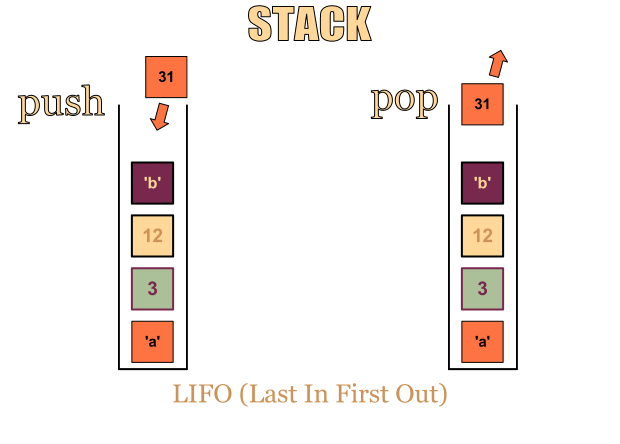
Stack như một chồng các phần tử, phần tử này nằm lên trên phần tử khác. Ta có thể push/thêm một phần tử mới vào stack bằng cách đặt nó lên trên phần từ trên cùng của stack. Ngược lại ta cũng có thể pop/ lấy ra một phần tử của trong stack ra bằng cách lấy đi phần tử trên cùng.

Phần tử được thêm vào cuối cùng, luôn là phần tử được lấy ra đầu tiên (LIFO, Last In First Out)

Mọi phép push hay pop, ta đều thao tác với phần tử dễ tiếp cận nhất của stack - phần tử nằm trên cùng, nên độ phức tạp của 2 phép này đều là O(1)

Queue

Tạm dịch: hàng đợi

Queue là một hàng các phần tử xếp liên tiếp nhau. Một phần tử mới được enqueue/thêm vào bằng cách xêp nó vào sau phần tử cuối cùng của hàng đợi. Ngược lại, ta có thể dequeue/ bỏ phần tử bằng cách lấy đi phần tử đầu tiên của hàng đợi. Nguyên lý vận hành của queue là: phần tử được thêm vào đầu tiên cũng là phần tử được lấy ra đầu tiên (FIFO, First In First Out)

Tương tự độ khó của phép euqueue và dequeue cũng là O(1).