Cấu trúc dữ liệu BIT – Binary Indexed Tree (Fenwick Tree)

1. Giới thiệu:

Ngày nay, mặc dù máy tính đã được nâng cấp trở lên mạnh mẽ, có thể tính toán hàng triệu, trăm triệu phép toán trong vòng 1 giây. Nhưng đối với nhiều bài toán có độ phức tạp cao, khó thì máy tính dù mạnh mẽ đến mấy cũng khó có thể đảm bảo có thể tính toán trong thời gian ngắn nhất.

Tôi đã từng giải 1 bài toán và để cho máy tính chạy hàng tiếng đồng hồ mà vẫn chưa ra kết quả, bởi vì phương pháp giải quyết bài toán của tôi không tốt, độ phức tạp quá lớn (On2). Nhiều lần như vậy, tôi đã phải bỏ thời gian, công sức để nghiên cứu về thuật toán và cấu trúc dữ liệu và tình trạng giải quyết bài toán của tôi đã được cải thiện lên rất nhiều. Ngày hôm nay, tôi xin phép được giới thiệu 1 cấu trúc dữ liệu khá thú vị là Cấu trúc dữ liệu Binary Indexed Tree (BIT) hay còn được biết đến với cái tên Frenwick Tree

BIT được sử dụng trong những bài toán về mảng, truy vấn trên mảng.

2. Ưu nhược điểm:

• Ưu điểm:
  1. Bộ nhớ thấp
  2. Cài đặt đơn giản
  3. Có thể giải được nhiều bài toán về dãy số
  4. Thời gian chạy: O(logn)
• Nhược điểm:

Không tổng quát bằng Segment Tree (Một cấu trúc dữ liệu giải thuật khác). Tất cả những bài giải được bằng Fenwick tree đều có thể giải được bằng Segment Tree. Nhưng chiều ngược lại thì không đúng

3. Mô tả về Frenwick Tree

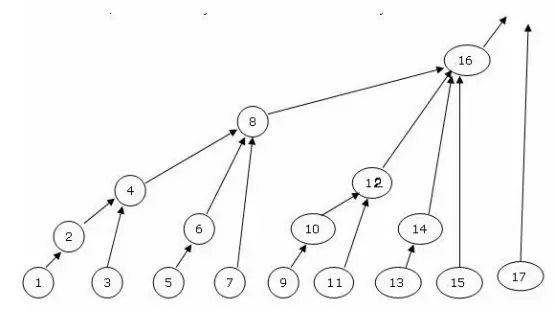
Hình 1: Các nút biểu diễn trong Frenwick tree

Đặt m = 2k.p (với p là số lẻ). Hay nói cách khác, k là vị trí của bít 1 bên phải nhất của m. Trong Fenwick-Tree, nút có số hiệu m sẽ là nút gốc của một cây con gồm 2k nút có số hiệu từ m- 2k+1 đến m.

• Nút 12: 12 = 22 x 3 . Vậy các nút nó sẽ quản lý là (12 - 22+1 = 9) cho đến (12) Nhìn trong hình đúng là nút 12 sẽ quản lý các nút 9,10,11,12
• Nút 17: 17 = 20 x 17 Vậy nút 17 chỉ quản lý bản thân nó là nút 17

4. Ví dụ bài toán cụ thể

Cho dãy số A có N phần tử, giá trị ban đầu của các phần tử bằng 0. Có 2 loại truy vấn cần thực hiện:

• Tăng giá trị ở phần tử thứ i lên 1 đơn vị (truy vấn 1)
• Tính tổng của mảng từ phần tử thứ 1 đến vị trí thứ i (truy vấn 2).

Mô tả yêu cầu:

• Nhập vào 2 giá trị n, m ( 1<= n,m <=106)
• Các dòng tiếp theo là các truy vấn có dạng [loại] [chỉ số phần tử]
  
  Yêu cầu in ra giá trị của loại truy vấn loại 2.

Input:
5 5
1 1
2 3
1 3
2 4
2 2

Output:
1
2
1

Ví dụ có thể hiểu như sau:

• Cho 1 mảng gồm 5 phần tử khởi tạo đều bằng 0
• Truy vấn thứ nhất: 1 1 => Tăng giá trị tại phần tử thứ nhất lên 1 đơn vị. Giá trị của mảng tại sau thời điểm đó: [1, 0, 0, 0, 0]
• Truy vấn thứ 2: 2 3 => In ra kết quả tổng phần tử từ thứ nhất đến thứ 3 => Kết quả = 1.
• Truy vấn thứ 3: 1 3 => Tăng giá trị tại phần tử thứ 3 lên 1 đơn vị. Giá trị của mảng tại sau thời điểm đó: [1, 0, 1, 0, 0]
• Truy vấn thứ 4: 2 4 => In ra kết quả tổng phần tử từ thứ nhất đến thứ 3 => Kết quả = 2.
• Truy vấn thứ 5: 2 2 => In ra kết quả tổng phần tử từ thứ nhất đến thứ 3 => Kết quả = 1.

Nhận xét:

Thông thường với bài toán như vậy ta sẽ thường giải với độ phức tạp rất lớn đối với thao tác tính tổng (Nếu tính tổng từ 1 -> n độ phức tạp với O(n)). Mà giới hạn của bài toán là n đến 106.. Nếu bài toán là mảng 106 và số truy vấn tính tổng là 105 chẳng hạn thì số phép toàn của chúng ta sẽ là k106105. Với số phép toán như vậy việc chúng ta chờ dài cổ là điều hiển nhiên. Vì vậy chúng ta cần dùng cấu trúc dữ liệu và các giải thuật để tính toán.

5. Lời giải cho bài toán

Gọi a là mảng đầu vào của bài toán (khởi tạo các phần tử =0). Để giải bài toán này ta dùng 1 mảng khác (mảng t) để lưu tổng với dạng như sau:

– t1 = a1 (t1 lưu tổng của phần tử thứ nhất của mảng a)
– t2 = a1 + a2 (t2 lưu tổng của phần tử thứ nhất và thứ 2 của mảng a)
– t3 = a3
– t4 = a1 + a2 + a3 + a4
– t5 = a5
– t6 = a5 + a6
– t7 = a7
– t8 = a1 + a2 + a3 + a4+ a5 + a6 + a7 + a8
– …
– t12 = a9 + a10 + a11 + a12

Dựa vào (hình 1) ta sẽ hiểu ra quy luật lưu trữ tổng mà định nghĩa ở trên.

Khi có mảng t lưu trữ tổng ta có thể dễ dàng tính tổng tm (từ phần tử 1 đến m)
Ví dụ:

• Để tính A15 (Tổng của 10 phần tử đầu), thay vì phải duyệt từ a1 đến a15, ta chỉ cần tính t8 + t12 + t14 + t15 .
• Để tính A10 (Tổng của 10 phần tử đầu) , chỉ cần tính t8 + t10
• Để tính A13 (Tổng của 13 phần tử đầu), chỉ cần tính t8 + t12 + t13

6. Cài đặt code

Ta sẽ dùng 2 phương thức sau để thực hiện truy vấn là

• update : tăng phần tử thứ i lên 1 đơn vị
• sum: tổng từ phần tử thứ 1 đến i

public class Test {
 
    public void update(int p, int val, int[] t, int n) {
        while (p <= n) {
            t[p] += val;
            p = p + (p & -p);
        }
    }
 
    public int sum(int p, int[] t) {
        int result = 0;
        while (p >= 1) {
            result = result + t[p];
            p = p - (p & -p);
        }
        return result;
    }
 
    public static void main(String args[]) {
        Test test = new Test();
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        int[] t = new int[n + 1];
        for (int i = 1; i <= m; i++) {
            int x = scanner.nextInt();
            int y = scanner.nextInt();
            if (x == 1) {
                test.update(y, 1, t, n);
            } else {
                System.out.println(test.sum(y, t));
            }
        }
    }
}

Lưu ý phép toán p&-p <=> 2k mà trong lý thuyết đã nhắc tới

Cám ơn các bạn đã theo dõi bài viết của mình