Các thuật toán sắp xếp
Bài đăng này đã không được cập nhật trong 6 năm
Merge sort
Giống như Quick sort, Merge sort là thuật toán chia để trị. Chia mảng thành các mảng nhỏ, sau đó gộp các mảng nhỏ đã sắp xếp lại với nhau.
Ví dụ với mảng 38, 27, 43, 3, 9, 82, 10, trình tự của merge sort sẽ như sau:
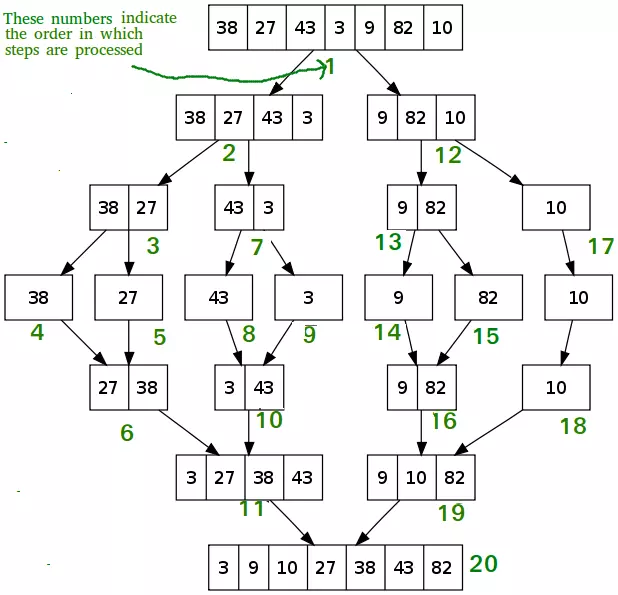
Triển khai thuật toán: Vì merge sort là một thuật toán sử dụng rất nhiều bộ nhớ nên sẽ tốt hơn khi sử dụng linked list, với linked list thì việc tách mảng và lưu trữ sẽ đơn giản hơn rất nhiều so với sử dụng mảng thông thường (Bạn cần có kiến thức cơ bản về con trỏ trước khi xem đoạn code dưới).
// C++ code for linked list merged sort
#include <bits/stdc++.h>
using namespace std;
/* Link list node */
class Node {
public:
int data;
Node* next;
};
/* function prototypes */
Node* SortedMerge(Node* a, Node* b);
void FrontBackSplit(Node* source, Node** frontRef, Node** backRef);
void MergeSort(Node** headRef)
{
Node* head = *headRef;
Node* a;
Node* b;
/* Điều kiện dừng, khi linked list có 0 hoặc 1 node */
if ((head == NULL) || (head->next == NULL)) {
return;
}
/* Chia thành 2 linked list nhỏ a, b*/
FrontBackSplit(head, &a, &b);
/* Đệ quy để chia thành các linked list nhỏ nhất */
MergeSort(&a);
MergeSort(&b);
/* answer = merge the two sorted lists together */
*headRef = SortedMerge(a, b);
}
/* Trộn 2 mảng đã được sắp xếp */
Node* SortedMerge(Node* a, Node* b)
{
Node* result = NULL;
if (a == NULL)
return (b);
else if (b == NULL)
return (a);
if (a->data <= b->data) {
result = a;
result->next = SortedMerge(a->next, b);
}
else {
result = b;
result->next = SortedMerge(a, b->next);
}
return (result);
}
/* Chia đôi linked list source thành frontRef và backRef */
void FrontBackSplit(Node* source,
Node** frontRef, Node** backRef)
{
Node* fast;
Node* slow;
slow = source;
fast = source->next;
/* Node fast di chuyển 2 bước thì Node slow di chuyể n được 1 bước */
while (fast != NULL) {
fast = fast->next;
if (fast != NULL) {
slow = slow->next;
fast = fast->next;
}
}
/* Cuối cùng Note slow sẽ là Node ở giữa */
*frontRef = source;
*backRef = slow->next;
slow->next = NULL;
}
void printList(Node* node)
{
while (node != NULL) {
cout << node->data << " ";
node = node->next;
}
}
/* Hàm thêm 1 node vào đầu mỗi linked list */
void push(Node** head_ref, int new_data)
{
Node* new_node = new Node();
new_node->data = new_data;
new_node->next = (*head_ref);
(*head_ref) = new_node;
}
int main()
{
Node* a = NULL;
/* Tạo linked list: 2->3->20->5->10->15 */
push(&a, 15);
push(&a, 10);
push(&a, 5);
push(&a, 20);
push(&a, 3);
push(&a, 2);
/* Sử dụng merge sort */
MergeSort(&a);
cout << "Sorted Linked List is: \n";
printList(a);
return 0;
}
// This is code is contributed by rathbhupendra
Counting sort
Counting sort là một kỹ thuật sắp xếp các đối tượng trong một phạm vị cụ thể. Nó hoạt động bằng cách đếm số lượng các đôi tượng có giá trị giống nhau. Sau đó sử dụng một chút toán học để tính toán vị trí cuối cùng của đối tượng đó.
Độ phức tạp của thuật toán này là O(n+k) với n là số lượng đối lượng, k là phạm vị giá trị của n đối tượng.
Hãy tìm hiểu thông qua 1 ví dụ:
Phạm vị giá trị k 10, giá trị của n nằm trong đoạn từ [0, 9].
Input: 1, 4, 1, 2, 7, 5, 2
1) Đếm số lượng các đối tượng có giá trị giống nhau.
Index: 0 1 2 3 4 5 6 7 8 9
Count: 0 2 2 0 1 1 0 1 0 0
2) Sửa lại giá trị của mảng Count sao cho giá trị tại mỗi vị trí i sẽ bằng tổng giá trị tại vị trí i + giá trị tại vị trí i - 1.
Index: 0 1 2 3 4 5 6 7 8 9
Count: 0 2 4 4 5 6 6 7 7 7
Giá trị của mảng Count sẽ chỉ ra vị trí cuối cùng của các đối tượng.
3) Sắp xếp lại các phần tử vào mảng Output.
Với Input là: 1, 4, 1, 2, 7, 5, 2. Vị trí của 1 là 2 trong mảng Output.
Giảm giá trị tại vị trí 1 của mảng Count xuống 1 đơn vị
Giá tiếp theo là 4, vị trí trong mảng Output là 5. Giảm giá trị tại vị trí 4 của mảng Count xuống 1 đơn vị
Cứ như vậy và ta sẽ thu được kết quả của mảng Output là : 1, 1, 2, 2, 4, 5, 7
Triển khai thuật toán:
// C++ Program for counting sort
#include<bits/stdc++.h>
#include<string.h>
using namespace std;
k = 256
#define RANGE 255
void countSort(char arr[])
{
// Mảng Output
char output[strlen(arr)];
// Mảng count với 256 phần tử từ 0-255 với giá trị là 0 tại mỗi vị trí
int count[RANGE + 1], i;
memset(count, 0, sizeof(count));
// Đếm số lượng đối tượng có cùng giá trị và lưu kết quả vào mảng count
for(i = 0; arr[i]; ++i)
++count[arr[i]];
// Thay đổi giá trị của mảng count
for (i = 1; i <= RANGE; ++i)
count[i] += count[i-1];
// Xây dựng mảng Output
for (i = 0; arr[i]; ++i)
{
output[count[arr[i]]-1] = arr[i];
--count[arr[i]];
}
for (i = 0; arr[i]; ++i)
arr[i] = output[i];
}
// Driver code
int main()
{
char arr[] = "geeksforgeeks";
countSort(arr);
cout<< "Sorted character array is " << arr;
return 0;
}
// This code is contributed by rathbhupendra
Đây là một đoạn code sắp xếp mảng các ký tự, thuật toán cũng có thể được sử dụng để sắp xếp mảng các số nguyên. Với mảng các số nguyên bao gồm cả số âm và dương thì cần phải thay đổi thuật toán 1 chút. Lí do là vì trong c++ bạn không thể truy cập giá trị tại ví trí âm trong mảng. Để giải quyết vấn đề này bạn cần tính lại khoảng k và xây dựng lại mảng count sao cho phần tử nhỏ nhất ở trị trí 0.
Radix sort
Các thuật toán quen thuộc như quick sort, merge sort, heap sort,... là các thuật toán sắp xếp dựa vào giá trị của các phép so sánh, độ phức tạo của các thuật toán này không thể tốt hơn O(nLogn). Còn với thuật toán counting sort ở trên, là một thuật toán tuyến tính với độ phức tạp là O(n+k). Trong trường hợp k bằng n*n thì counting sort là một lựa chọn tồi. Radix sort là một lựa chọn tốt trong TH này.
Tư tưởng của thuật toán này là sắp xếp các số theo giá trị của hàng chục, hàng trăm, hàng nghìn, ...
Ví dụ:
với một mảng các số 170, 45, 75, 90, 802, 24, 2, 66
Đầu tiên sắp xếp theo hàng đơn vị
170, 90, 802, 2, 24, 45, 75, 66
0 0 2 2 4 5 5 6
Tiếp theo đến hàng chục
802, 2, 24, 45, 66, 170, 75, 90
0 0 2 4 6 7 7 9
Cứ như vậy sẽ thu được kết quả cuối cùng
2, 24, 45, 66, 75, 90, 170, 802
Triển khai thuật toán:
// C++ implementation of Radix Sort
#include<iostream>
using namespace std;
// Tìm giá trị lớn nhất trong mảng
int getMax(int arr[], int n)
{
int mx = arr[0];
for (int i = 1; i < n; i++)
if (arr[i] > mx)
mx = arr[i];
return mx;
}
// Sử dụng thuật toán counting sort để sắp xếp lại vị trí của các đôi tượng theo giá trị hàng đơn vị, hàng chục,...
void countSort(int arr[], int n, int exp)
{
int output[n];
int i, count[10] = {0};
for (i = 0; i < n; i++)
count[ (arr[i]/exp)%10 ]++;
for (i = 1; i < 10; i++)
count[i] += count[i - 1];
for (i = n - 1; i >= 0; i--)
{
output[count[ (arr[i]/exp)%10 ] - 1] = arr[i];
count[ (arr[i]/exp)%10 ]--;
}
for (i = 0; i < n; i++)
arr[i] = output[i];
}
// Radix Sort
void radixsort(int arr[], int n)
{
int m = getMax(arr, n);
// Sử dụng couting sort để sắp xếp lại vị trí các đôi tượng
for (int exp = 1; m/exp > 0; exp *= 10)
countSort(arr, n, exp);
}
void print(int arr[], int n)
{
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
}
int main()
{
int arr[] = {170, 45, 75, 90, 802, 24, 2, 66};
int n = sizeof(arr)/sizeof(arr[0]);
radixsort(arr, n);
print(arr, n);
return 0;
}
Bài viết tham khảo:
All rights reserved