Cây là một loại cấu trúc dữ liệu có dạng là tập hợp các nút (node), được liên kết với nhau theo quan hệ cha con. Có rất nhiều loại cây, với các quy tắc sắp xếp node khác nhau.

Sau đây, mình xin giới thiệu một vài loại cây.

1. Cây cơ bản

Định nghĩa

Là cấu trúc dữ liệu cây mà không có ràng buộc giữa các node. Một node cha có thể có nhiều node con.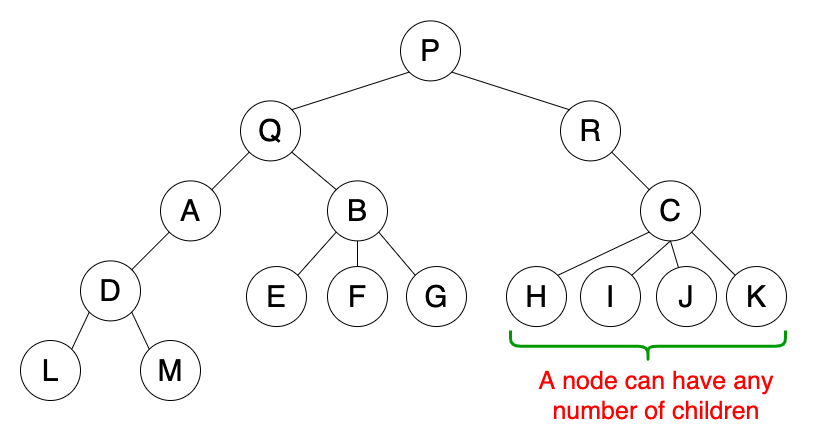

Ứng dụng

Cây cơ bản được sử dụng trong việc biểu diễn dữ liệu có dạng cấp bậc như cấu trúc folder,...

2. Cây nhị phân

Định nghĩa

Một cây mà mỗi node có không quá 2 node con thì được gọi là cây nhị phân.

Node con bên trái được gọi là Node con trái (left child), node con bên phải được gọi là Node con phải (right child).

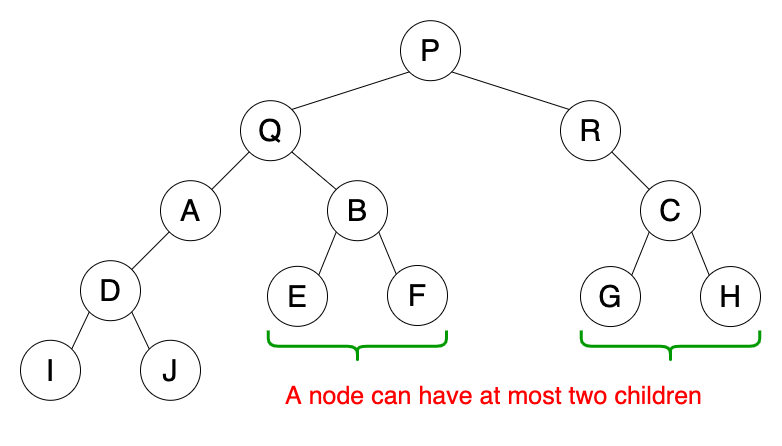
• Cây nhị phân mà mỗi đỉnh trong có đúng hai con được gọi là "cây nhị phân đầy đủ" (full binary tree).
• Cây nhị phân đầy đủ mà tất cả các lá có cùng độ sâu được gọi là “cây nhị phân hoàn chỉnh” (perfect binary tree).
• Cây nhị phân mà mỗi đỉnh của nó đã có con phải thì cũng có con trái được gọi là cây nhị phân gần hoàn chỉnh (almost complete binary tree).

3. Cây nhị phân tìm kiếm

Cây nhị phân tìm kiếm - Binary Search Tree là một kiểu cấu trúc dữ liệu được sử dụng rất nhiều.

Định nghĩa

Là một loại cây nhị phân có ràng buộc giữa các node như sau: giá trị node con trái < giá trị node cha < giá trị node con phải.

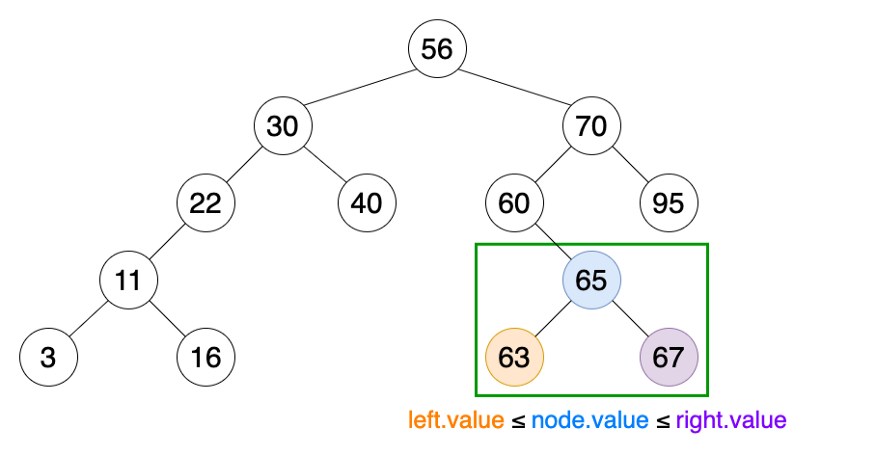
Ứng dụng

• Lưu trữ dữ liệu dưới dạng sắp xếp, giúp cho việc tìm kiếm một node bất kì trở nên dễ dàng hơn.
• Biểu diễn các biểu thức số học.
• Được dùng trong nhân Unix để quản lý vùng nhớ ảo.

4. Đống (Heap)

Định nghĩa

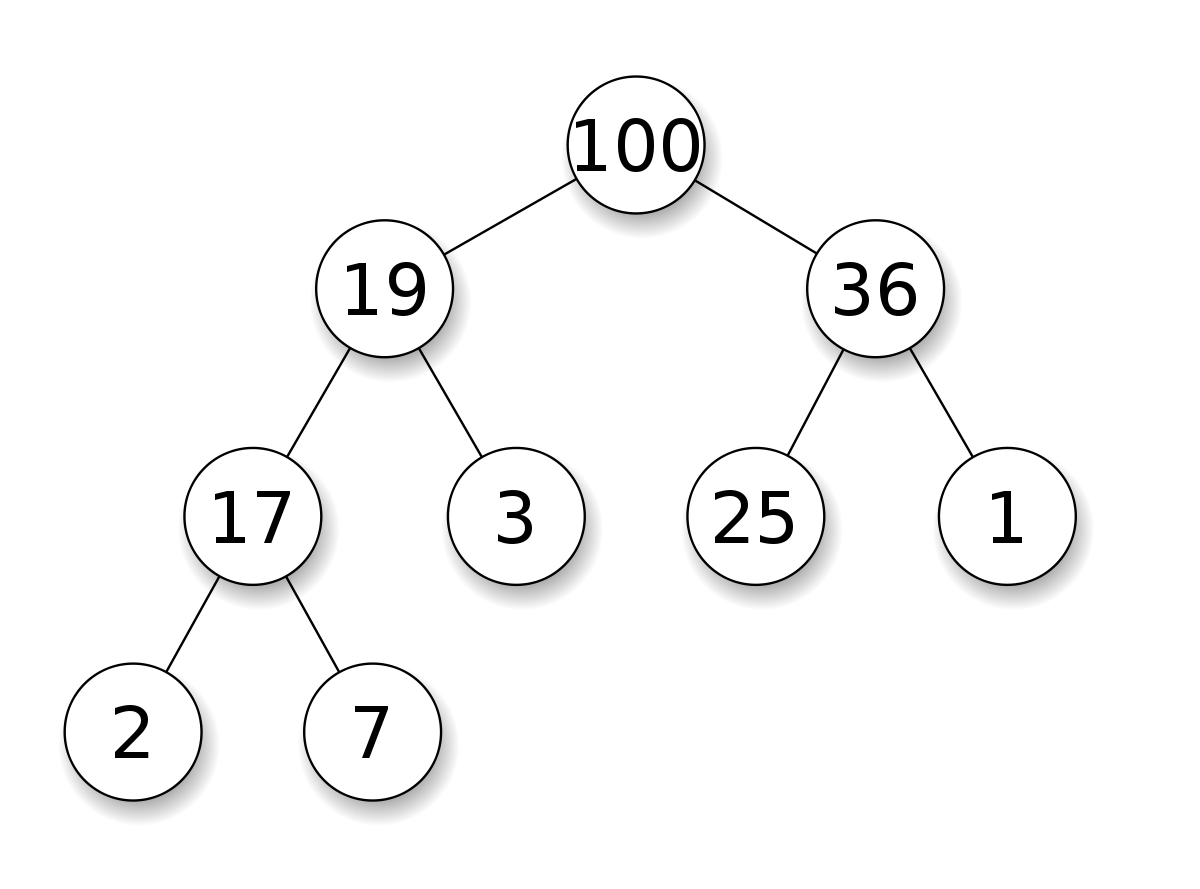
Cây nhị phân được gọi là đống nếu giá trị của các node thỏa mãn điều kiện sau:

Giá trị của phần tử cha > giá trị phần tử con (Đống cực đại)

hoặc

Giá trị phần tử cha < giá trị phần tử con (Đống cực tiểu)

Ứng dụng

• Sử dụng trong thuật toán Dijkstra (tìm đường đi ngắn nhất).
• Sử dụng trong các bài toán cần tìm giá trị lớn nhất/nhỏ nhất một cách nhanh chóng.

5. Cây AVL

Định nghĩa

Cây AVL (tên ba nhà phát minh Adelson, Velski và Landis) là cây tìm kiếm nhị phân có tính chất tự cân bằng.

Hiệu số của độ cao của các cây con bên trái và cây con bên phải được gọi là Balance Factor (Nhân tố cân bằng). Cây AVL đảm bảo rằng Balance Factor không lớn hơn 1. Trong cây AVL, phép chèn (insertion), và xóa (deletion) luôn chỉ tốn thời gian O(log n) trong cả trường hợp trung bình và trường hợp xấu nhất.

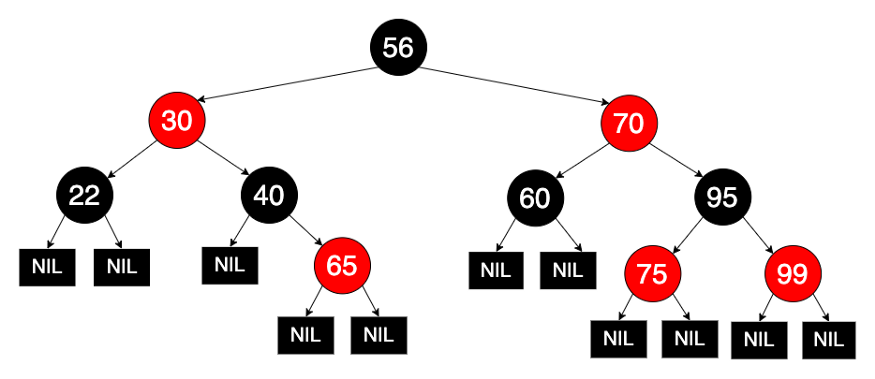
6. Cây đỏ đen

Định nghĩa

Cây đỏ đen là một dạng cây tìm kiếm nhị phân tự cân bằng, đảm bảo một số tính chất sau:

• Mọi node trong cây phải là đỏ hoặc đen.
• Node gốc là đen.
• Tất cả các lá (NULL) là đen.
• Mọi node đỏ đều có node con là đen.
• Tất cả các đường đi từ một nút bất kỳ tới các lá phải đi qua số nút đen bằng nhau.

Ứng dụng

• Được sử dụng trong Completely Fair Scheduler (bộ lập lịch được sử dụng trong nhân Linux).
• Mysql sử dụng cây đỏ đen cho chỉ mục ở trong bảng.
• Được sử dụng trong thuật toán phân cụm K-mean để giảm độ phức tạp về thời gian.

Tài liệu tham khảo

1. https://vi.wikipedia.org/wiki/Cây_(lý_thuyết_đồ_thị)#Cây_nhị_phân
2. https://www.geeksforgeeks.org/red-black-tree-set-1-introduction-2/
3. https://towardsdatascience.com/8-useful-tree-data-structures-worth-knowing-8532c7231e8c
4. https://vi.wikipedia.org/wiki/Cây_AVL#Phép_xóa_trên_cây_AVL