Bitonic Sort

Sorting data efficiently and rapidly is one of the hot talk among the computer science engineers. Several effective algorithms are created to do so, yet more research are undergoing to reach the linear time mark. Today our discussion will be on Bitonic sort, a not very well-known algorithm, is a parralel algorithm that you never hear about probalbly.

Bitonic Sort

Very few sortings are as fast as bitonic sorting network in this computing world . A sorting network is an exceptional kind of sorting algorithm, where the comparison sequence is not dependent on data. This makes sorting networks suitable for implementing in hardware or in parallel processor arrays.The sorting network bitonic sort consists of Θ(n·log(n)2) comparators. It has the same asymptotic complexity as odd-even mergesort and shellsort. Although a sorting network with only O(n·log(n)) comparators is known, due to its large constant it is slower than bitonic sort for all practical problem sizes. In the following, bitonic sort is developed on the basis of the 0-1-sequence principle. The 0-1-principle states that a comparator network that sorts every sequence of 0's and 1's is a sorting network, i.e. it sorts every sequence of arbitrary values.

Bitonic Sequence

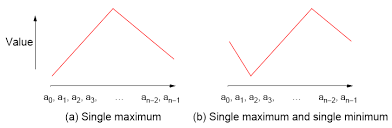
A sequence list = (a1, a2, . . ., ap) of p numbers is said to be bitonic if and only if

• a1 ≤ a2 ≤ . . . ≤ ak ≥ . . . ≥ ap, for some k, 1 < k < p, or
• a1 ≥ a2 ≥ . . . ≥ ak ≤ . . . ≤ ap, for some k, 1 < k < p
• p can be divided into two portions that can be swapped to give either of the first two cases or,
• There cannot be more than one local maximum and not more than one local minimum

Algorithm steps

Following are the generelised steps for bitonic sort

• Input: Number of processors, Data length
• Search the ranks of each processor
• Fill data in each processor using randomize function
• Sort the lists generated in the processor
• Bitonic sequences of size 2 are merged to create ordered lists of size 2. At the end of this first stage of merging, we actually have n/4 bitonic sequences of size 4.
• Bitonic sequences of size 4 are merged into sorted sequences of size 4, alternately into increasing and decreasing order, so as to form n/8 bitonic sequences of size 8 and so on.
• Given an unordered sequence of size 2n, exactly log2 2n stages of merging are required to produce a completely ordered list.
• The above steps use comparison functions to compare and exchange
• Output: ordered list

Implementation

Below is the ruby implementation of bitonic sort.

def bitonic_sort up, list
  list_length = list.size
  return list if list_length <= 1 
  first = bitonic_sort true, x[0...list_length / 2]
  second = bitonic_sort false, x[list_length / 2...list_length]
  bitonic_merge up, first + second
end

def bitonic_merge up, list
  list_length = list.size
  return list if list_length == 1 
  bitonic_compare up, list
  first = bitonic_merge(up, x[0...list_length / 2])
  second = bitonic_merge(up, x[list_length / 2...list_length])
  first + second
end

def bitonic_compare up, list
  distance = list.size / 2
  for i in (0...distance) do
    x[i], x[i + distance] = x[i + distance], x[i] if (x[i] > x[i + distance]) == up 
  end
end

Efficiency

When executed in serial, the bitonic sorting network finishes its work in O(n log2n) comparisons, which is way shorter of the usual comparison-based sort efficiency of O(n log n). However, Parallel versions of this sort can cause dramatic speedups, yet it rely on the implementation.

Bitonic sort is a very strong, rapid and powerful sorting algorithm which focuses mainly on parralelism. But you have to understand that it is not feasible for all the cases. So if you are interested more, you need to study more to understand its usage.

Reference: https://en.wikipedia.org/wiki/Bitonic_sorter