Binary Search Trees in Swift
Bài đăng này đã không được cập nhật trong 6 năm
Tiếp tục với series về Data Structures bài viết này chúng ta cùng tìm hiểu về Binary Search Trees
Binary Search Trees là một trong những cấu trúc dữ liệu cơ bản nhất trong khoa học máy tính. Chúng rất hiệu quả khi chèn và tìm kiếm các phần tử. Trong bài viết này, chúng ta sẽ tìm hiểu và sẽ triển khai cây tìm kiếm nhị phân trên ngôn ngữ swift.
Trees, Nodes and Links
Khi bạn nghe mọi người nói về cây tìm kiếm nhị phân, bạn sẽ nghe thấy các thuật ngữ như: root, left child, right child, node, link, subtree… , dưới đây là 1 sơ đồ để mô tả những thuật ngữ trên:
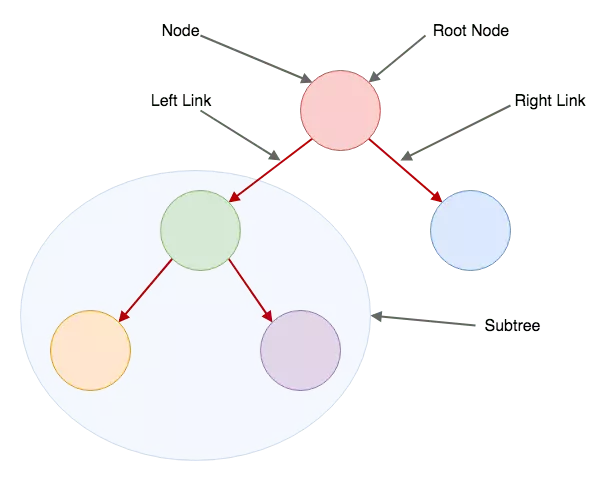
Cây nhị phân bao gồm các nút. Mỗi nút chỉ có thể có hai con. Họ có thể có một nút con trái hoặc phải. Kết nối giữa nút và con của nó được gọi là 'link'. Vì vậy, một nút có thể có một trái và một liên kết bên phải, trỏ đến một trái hoặc một phần tử con bên phải.
Một nút mà liên kết bên trái hoặc bên phải của bạn trỏ tới có thể, lần lượt, có các phần tử con riêng của nó. Và cứ thế. Nút đầu tiên trong cây được gọi là nút 'root'. Thông thường đây là nút đầu tiên được chèn vào một cây nhị phân, nhưng nhiều hơn về sau đó. Một nút không phải là nút gốc và được trỏ đến có thể được gọi là "subtree". Một cây con bao gồm nút gốc và con của nó. Ví dụ, nút màu xanh lá cây trên biểu đồ của chúng tôi là nút gốc, và tất cả các nút mà nút này trỏ tới (một cách chính xác hơn để nói - các nút có thể truy cập từ nút này) là một phần của cây con của nó.
Đối với bất kỳ nút nào trong cây, giá trị bên trái nhỏ hơn nút và con phải lớn hơn nút. Trong triển khai của chúng tôi, chúng tôi sẽ sử dụng khóa và giá trị. Bạn có thể sử dụng bất kỳ loại nào cho khóa, miễn là nó có thể so sánh và bạn có thể sử dụng bất kỳ loại nào cho giá trị.
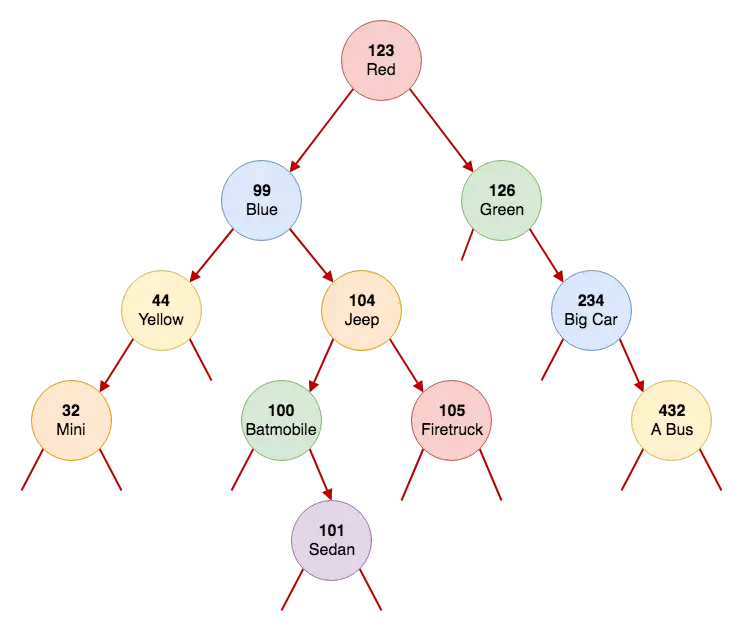
Đây là một ví dụ về cây nhị phân mà chúng ta sẽ xây dựng trong bài viết này:
A Bit Of Code
Như đã nêu ở trên, biểu đồ của chúng tôi sẽ bao gồm các nút và một nút sẽ có một khóa, giá trị, trái và một liên kết phù hợp. Một nút sẽ là một lớp chung, miễn là các khóa phù hợp với giao thức có thể so sánh. Lớp nút trông giống như sau:
class Node<Key: Comparable, Value> {
var key: Key
var value: Value
var left: Node?
var right: Node?
init(key: Key, value: Value) {
self.key = key
self.value = value
}
}
Các liên kết bên trái và bên phải trong nút của chúng tôi là loại ‘Node’ vì chúng trỏ đến các nút khác trên cây. Chúng có thể là 0 vì một nút không cần phải có chúng. Nếu nút không có con, nút này được gọi là nút lá ‘Leaf’. Hãy xem cách lớp đơn giản này phù hợp với việc thực thi cây tìm kiếm nhị phân của chúng tôi.
Binary Search Tree
Điều quan trọng cần nhớ về cây tìm kiếm nhị phân là nút bên trái nhỏ hơn nút hiện tại và nút phải lớn hơn. Chúng tôi sẽ triển khai các hoạt động CRUD chuẩn trên cây và tất cả chúng sẽ xoay quanh nguyên tắc đơn giản này.
Searching
Chúng ta sẽ so sánh khóa với nút hiện tại và nếu khóa chúng ta đang tìm kiếm nhỏ hơn, chúng ta biết chúng ta nên nhìn vào bên trái của con. Nếu con trái là không, thì chìa khóa không tồn tại trong cây. Điều ngược lại là đúng. Hãy kiểm tra code:
public func get(key: Key) -> Value? {
return get(node: root, key: key)
}
private func get(node: Node<Key, Value>?, key: Key) -> Value? {
guard let aNode = node else {
return nil
}
if key < aNode.key {
return get(node: aNode.left, key: key)
} else if key > aNode.key {
return get(node: aNode.right, key: key)
} else {
return aNode.value
}
}
Bây giờ, sẽ tìm hiểu một chút về đệ quy ...
Recursion
Bạn có thấy một hàm tự gọi với các thông số khác nhau. Một chức năng gọi chính nó là những gì chúng ta gọi là một cuộc gọi đệ quy (hoặc đệ quy chức năng, hoặc đơn giản, đệ quy). Hàm đệ quy có thể đơn giản hóa code của bạn rất nhiều. Phần quan trọng nhất của hàm đệ quy là điều kiện thoát. Chức năng của bạn phải có đường dẫn mà nó có thể thực hiện mà nó sẽ không tự gọi. Trong đoạn mã trên chúng ta có hai điều kiện thoát. Nếu bạn không cẩn thận với điều kiện thoát , hoặc nếu điều kiện thoát của bạn không thỏa mãn, bạn sẽ kết thúc trong vòng lặp vô hạn.
Đây là đệ quy trên biểu đồ:
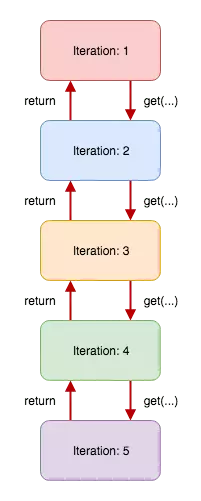
Trong ‘Iteration 1’, chúng ta gọi hàm ‘get’ và trả về kết quả của nó. Hãy tưởng tượng rằng trong 'Iteration 5' chúng ta đã đạt được điều kiện thoát của chúng ta (khóa bằng với nút chúng ta đang kiểm tra trong 'Iteration 5'), chúng ta trả về giá trị đó là 'Iteration 4' và giá trị sẽ tăng lên thành 'Iteration 1'.
Min And Max
Cây tìm kiếm nhị phân được sắp xếp. Nếu bạn nhìn vào sơ đồ của cây ở trên, bạn sẽ nhận thấy rằng phần tử bên trái nhất sẽ luôn là phần tử nhỏ nhất trong cây và tận cùng bên phải sẽ luôn là phần tử lớn nhất. Chúng ta có thể dễ dàng thực hiện các hàm min và max. Ví dụ, đây là một hàm min trông như thế nào:
private func min(node: Node<Key, Value>) -> Node<Key, Value> {
guard let leftNode = node.left else {
return node
}
return min(node: leftNode)
}
Tất cả những gì chúng tôi đang làm là tiếp tục di chuyển sang trái. Nếu nút hiện tại không có phần tử con trái, chúng tôi đã tìm thấy số lượng tối thiểu và trả lại. Đối với hàm tối đa bạn sẽ làm ngược lại.
Inserting
Các yếu tố mới được chèn vào ở dưới cùng của cây. Khi chúng tôi chèn phần tử mới vào cây, chúng tôi bắt đầu từ gốc cây và so sánh phần tử mới với nút mà chúng tôi hiện đang quan sát. Ví dụ: nếu khóa mới nhỏ hơn khóa của nút gốc, chúng tôi sẽ di chuyển sang bên trái. Chúng tôi lặp lại quá trình này cho đến khi chúng tôi không thể di chuyển sang trái hoặc phải nữa. Cho đến khi nút trái hoặc phải là không. Sau đó, chúng ta tạo một nút mới trong cây và thiết lập nó như là một nút con của nút trước đó.
public func put(key: Key, value: Value) {
root = put(node: root, key: key, value: value)
}
private func put(node: Node<Key, Value>?, key: Key, value: Value) -> Node<Key, Value> {
guard let aNode = node else {
return Node<Key, Value>(key: key, value: value)
}
if key < aNode.key {
aNode.left = put(node: aNode.left, key: key, value: value)
} else if key > aNode.key {
aNode.right = put(node: aNode.right, key: key, value: value)
} else {
aNode.value = value
}
return aNode
}
Chúng ta đang chèn đối tượng ‘car’ vào cây . Chúng ta đã có một đối tượng trong cây, đó sẽ là nút gốc. Nút gốc sẽ có khóa ‘123’ và ô tô có tên ‘Red’. Nếu chúng ta chèn một chiếc xe ‘Blue’ mới có khóa '99', chúng ta sẽ gọi hàm ‘put’. Hàm sẽ gọi phương thức ‘put’ đệ quy (nhánh ‘if’ đầu tiên trong danh sách ở trên), chuyển vào nút bên trái của nó (không phải là nil) và gán kết quả của lời gọi hàm tới nút bên trái. Khi phương thức 'put' đó được gọi với tham số nil, nó sẽ nhấn vào điều kiện thoát và tạo ra một nút mới với khóa và giá trị được truyền vào.
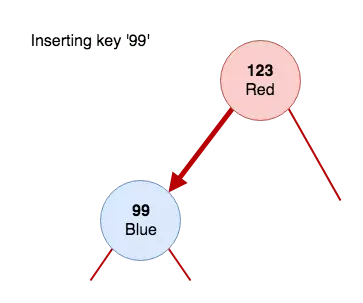
Nếu chúng tôi muốn chèn một khóa '104', sơ đồ sẽ trông như sau:
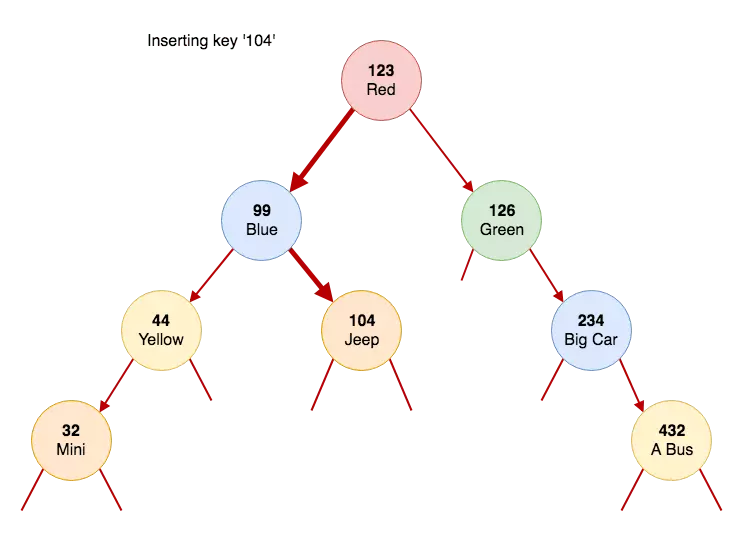Nó có thể giúp bạn hình dung được sự đệ quy như thế này… Bạn sẽ gọi phương thức ‘put’ một lần cho mỗi nút, nhiều nhất. Trong nút ‘123’, bạn gọi là ‘put’ và chuyển qua nút '99 ’đến nút đó. Từ đó, bạn gọi cho nút '104' và truyền con đúng của nút '99'. Vì nút '104' chưa tồn tại, bạn tạo nó và trả lại cho người gọi. Bây giờ nút '99' đã đưa con trỏ đến nút '104' và gán nó cho đúng biến con.
Deleting
Xóa một nút từ cây có thể hơi phức tạp một chút. Khi bạn xóa một nút, bạn cần giữ cho cây trong trạng thái được sắp xếp. Người đầu tiên đề xuất giải pháp cho vấn đề này là Hibbard vào năm 1962. Giải pháp của ông là thay thế nút với người kế nhiệm của nó.
Để hiểu đầy đủ thuật toán xóa Hibbard, trước hết chúng ta sẽ đi qua một bước cụ thể của thuật toán. Xóa tối thiểu. Hãy kiểm tra code để xóa nút tối thiểu.
private func deleteMin(node: Node<Key, Value>) -> Node<Key, Value>? {
guard let leftNode = node.left else {
return node.right
}
node.left = deleteMin(node: leftNode)
return node
}
Chúng tôi tiếp tục đi bên trái để tìm kiếm một nút tối thiểu. Khi chúng tôi tìm thấy nút tối thiểu của mình, chúng tôi chỉ cần trả lại đúng con của nó. Trả lại đúng con thành nút cha có hiệu quả cắt nút này ra khỏi cây. Bởi vì bây giờ node cha đang trỏ đến đúng con của nút mà chúng ta vừa xóa, nút đã xóa không có cha mẹ trỏ đến nó. Nếu đúng con là không, điều này có nghĩa là nút này không có con, vì vậy chúng ta sẽ trả về nil cho node cha.
Chúng ta sẽ xóa nút '99'. Sau khi chúng ta tìm thấy nút, tìm node kế nhiệm của nó. Node thừa kế là nút lớn hơn kế tiếp. Trong trường này, đó là nút có khóa '100'. Những gì làm là tìm mức tối thiểu trong nhánh phải của nút '99'. Sau đó xóa nút đó khỏi cây và thay thế con trỏ trái và phải của nó để trỏ tới các nút trái và phải của nút '99'.
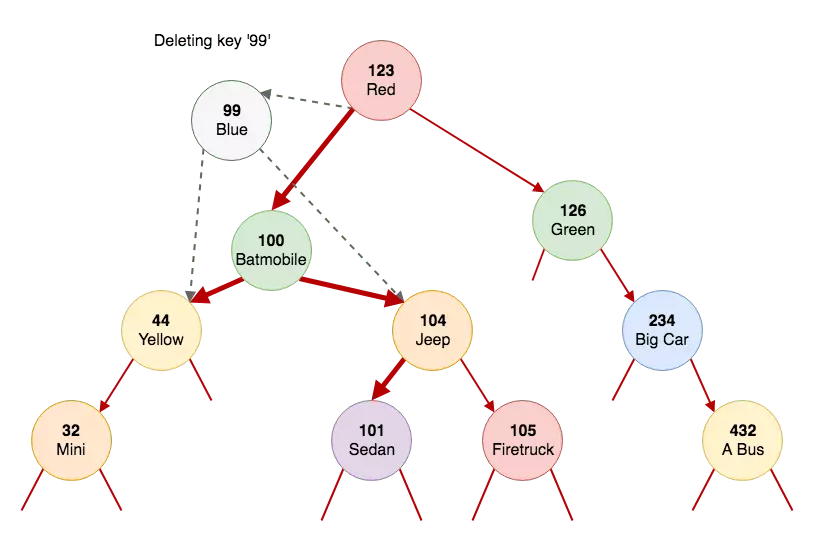
Nếu chúng ta nhìn vào nút '99', chúng ta biết rằng tất cả các nút ở bên trái nhỏ hơn '99' và tất cả các nút ở bên phải đều lớn hơn. Nếu chúng ta có nút nhỏ nhất ở phía bên phải của cây và thay thế nút '99' bằng cây đó, cây vẫn sẽ được sắp xếp. Và tất cả các nút ở bên phải sẽ vẫn lớn hơn nút mới.
private func delete(node: Node<Key, Value>?, key: Key) -> Node<Key, Value>? {
guard var aNode = node else {
return nil
}
if key < aNode.key {
aNode.left = delete(node: aNode.left, key: key)
} else if key > aNode.key {
aNode.right = delete(node: aNode.right, key: key)
} else {
guard let rightNode = aNode.right else {
return aNode.left
}
guard let leftNode = aNode.left else {
return aNode.right
}
aNode = min(node: rightNode)
aNode.right = deleteMin(node: rightNode)
aNode.left = leftNode
}
return aNode
}
Code để xóa một nút nằm trong nhánh 'else'. Chúng tôi tìm kiếm mức tối thiểu và gán cho biến cục bộ của chúng tôi. Tiếp theo, chúng ta xóa mức tối thiểu từ cây con phải và gán kết quả của hàm đệ quy cho con phải của nút mới (nút '100'). Trong bước cuối cùng, chúng tôi chỉ lấy con trái của nút '99' và gán nó cho con trái của nút '100'. Chúng tôi sẽ trả lại nút mới ‘100’ cho người gọi (nút ‘123’). Và người gọi sẽ đặt nó là con trái của nó trong trường hợp của chúng tôi.
Subscript
Hãy thêm một chú cú pháp và triển khai chỉ số. Điều này sẽ làm cho cây tìm kiếm nhị phân của chúng tôi thuận tiện hơn nhiều khi sử dụng:
public subscript(key: Key) -> Value? {
get {
return get(key: key)
}
set {
if let value = newValue {
put(key: key, value: value)
} else {
delete(key: key)
}
}
}
Với điều này, cây tìm kiếm nhị phân của chúng ta sẽ hoạt động như một dictionary và nó sẽ rất dễ sử dụng.
Test
Chúng ta cần phải tạo nút gốc của chúng ta trước và sau đó tạo cây với nó:
private func testBST() {
let rootNode = Node(key: 123, value: Car("Red"))
let binaryTree = BinarySearchTree(rootNode)
binaryTree[99] = Car("Blue")
binaryTree[126] = Car("Green")
binaryTree[44] = Car("Yellow")
binaryTree[32] = Car("Mini")
binaryTree[234] = Car("Big car")
binaryTree[432] = Car("A bus")
binaryTree[104] = Car("Jeep")
binaryTree[100] = Car("Batmobile")
binaryTree[101] = Car("Sedan")
binaryTree[105] = Car("Firetruck")
print("::::::::::Testing subscript::::::::::")
print("Blue car: ", binaryTree[99]?.name)
binaryTree[99] = Car("Not Blue")
print("Blue car: ", binaryTree[99]?.name)
binaryTree[99] = nil
print("Blue car: ", binaryTree[99]?.name)
print("::::::::::Testing min/max::::::::::")
print("MIN car: ", binaryTree[binaryTree.min]?.name)
print("MAX car: ", binaryTree[binaryTree.max]?.name)
print("::::::::::Delete max::::::::::")
binaryTree[432] = nil
print("MAX car: ", binaryTree[binaryTree.max]?.name)
}
Sau đó, chúng ta chỉ bắt đầu thêm các đối tượng tùy chỉnh vào cây và xử lý cây như một dictionary. Đầu ra của giao diện điều khiển cho code ở trên trông giống như sau:
::::::::::Testing subscript::::::::::
Blue car: Optional("Blue")
Blue car: Optional("Not Blue")
Blue car: nil
::::::::::Testing min/max::::::::::
MIN car: Optional("Mini")
MAX car: Optional("A bus")
::::::::::Delete max::::::::::
MAX car: Optional("Big car")
Conclusion
Cây tìm kiếm nhị phân rất hiệu quả và thời gian chạy các thuật toán chạy trên chúng thường được đo bằng thời gian logarit. Điều đó đang được nói, bạn phải cẩn thận khi sử dụng chúng. Thứ tự mà bạn chèn các phần tử vào cây là quan trọng.
Nếu dữ liệu bạn đang cố gắng chèn vào cây được sắp xếp, cây của bạn sẽ chỉ có con phù hợp (hoặc trái). Bạn về cơ bản sẽ kết thúc với một danh sách liên kết. Do đó, nếu bạn biết rằng dữ liệu bạn sẽ chèn sẽ được sắp xếp theo khóa bạn đang sử dụng trong BST, thì cấu trúc dữ liệu này sẽ không phải là lựa chọn tốt nhất cho bạn. Một cây cân bằng sẽ là một lựa chọn tốt hơn, nhưng đó là một câu chuyện cho một ngày khác.
Bài viết này được dich theo bài viết cùng tên của tác giả Dejan Agostini, trong bài viết này đã tạo một triển khai đơn giản của một hình ảnh, để giúp bạn hiểu về Binary Search Trees. Bạn có thể tìm thấy tất cả source code trên GitLab.
All rights reserved
