Binary Heap

Binary Heap là 1 cây nhị phân có đủ 2 tính chất sau:

1. Là cây nhị phân hoàn chỉnh (tức là tất cả các tầng đều được điền đủ, ngoại trừ tầng cuối, và tầng cuối cần có càng nhiều phần tử bên trái càng tốt). Tính chất này giúp ta có thể implement Binary Heap bằng cách sử dụng 1 mảng để chứa nó.
2. Binary Heap phải là Max Heap hoặc Min Heap. Trong Min Heap, phần tử ở node cha phải là nhỏ hơn tất cả các phần tử ở node con. Max Heap tương tự như MinHeap.
   

Ví dụ Min Heap

                 10                      10
               /      \               /       \  
             20        100          15         30  
             /                      /  \        /  \
           30                     40    50    100   40

Biểu diễn Binary Heap

Binary Heap là một cây nhị phân hoàn chỉnh cho nên nó thường được biểu diễn dưới dạng một mảng.

• Root là Arr[0].

• Với mỗi Arr[i] trong mảng

  Arr [ (i - 1) / 2 ]	Là node cha
  Arr [ (2i) + 1 ]	Là node con bên trái
  Arr [ (2i) + 2 ]	Là node con bên phải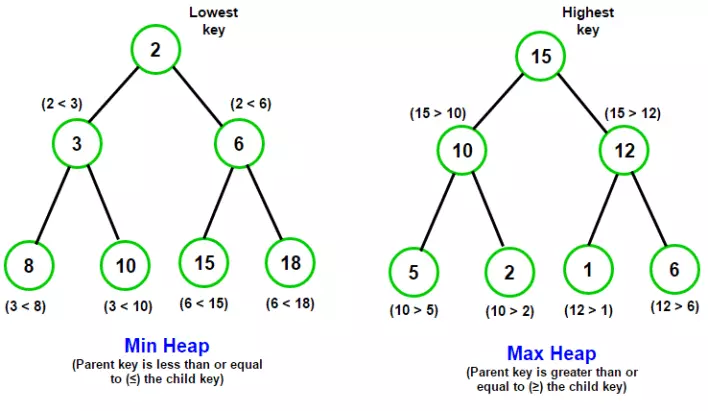

  

class MaxHeap
  attr_accessor :arr

  def initialize
    @arr = []
  end

  def swap(a, b)
    temp = arr[a]
    arr[a] = arr[b]
    arr[b] = temp
  end

  def parent i
    (i - 1) / 2
  end

  def left i
    i * 2 + 1
  end

  def right i
    i * 2 + 2
  end

  def extractMax
    root = arr[0]
    arr[0] = arr[arr.length - 1]
    arr.pop()
    MaxHeapify(0)
    return root
  end

  def deleteKey i
    arr[i] = MIN_INT
    # gán bằng min rồi đưa lên gốc
    while i != 0 and arr[parent(i)] < arr[i]
      swap(i, parent(i))
      i = parent(i)
    end
    # sau đó xóa
    extractMax()
  end

  def insertKey k
    arr.push(k)
    # đưa vào cuối mảng
    # sau đó sắp xếp lại thứ tự
    i = arr.length - 1
    while i != 0 and arr[parent(i)] < arr[i] do
        swap(i, parent(i))
        i = parent(i);
    end
  end

  def MaxHeapify i
    # đảm bảo các node từ node i->n đều có tính chất 2
    l = left(i)
    r = right(i)
    largest = i
    if l < arr.length and arr[l] > arr[i]
      largest = l
    end
    if r < arr.length and arr[r] > arr[largest]
      largest = r
    end
    if largest != i
      swap(i, largest)
      MaxHeapify(largest)
    end
  end
end

HeapSort

Heap sort là một kỹ thuật sắp xếp dựa trên cấu trúc dữ liệu Binary Heap. Nó tương tự như sắp xếp lựa chọn trong đó trước tiên chúng ta tìm phần tử lớn nhất (hoặc nhỏ nhất) và đặt phần tử đó ở cuối (hoặc đầu, tùy ý).

Heap Sort cho sắp xếp từ nhỏ đến lớn

1. Tạo Max Heap chứa toàn bộ phần tử cần sắp xếp
2. Lúc này, phần tử lớn nhất nằm ở root của heap, đổi chỗ nó về cuối mảng, giảm size của heap đi 1, sau đó heapify lại heap bỏ qua phần tử cuối mảng.
3. Lặp lại bước 2 cho đến hết heap.

def swap(arr, a, b)
  temp = arr[a]
  arr[a] = arr[b]
  arr[b] = temp
end

def heapify arr, n, i
  l = 2*i + 1 # left child's position
  r = 2*i + 2 # right child's position
  largest = i
  if l < n and arr[l] > arr[i]
    largest = l
  end
  if r < n and arr[r] > arr[largest]
    largest = r
  end
  if largest != i
    swap(arr, i, largest)
    heapify(arr, n, largest)
  end
end

def heapSort arr, n
  # đầu tiên phải heapify cho đúng tính chất 2 (phần tử cha lớn hơn phần tử con)
  # bắt đầu từ tầng gần cuối, vì tầng cuối ko có con.
  for i in (n/2 - 1).downto(0)
    heapify(arr, n, i)
  end

  # lấy phần tử lớn nhất của heap (tức arr[0]) đổi chỗ về cuối mảng rồi ko quan tâm đến nó nữa
  # sau đó heapify lại heap(lúc này số lượng phần tử trong heap đã giảm đi 1)
  # lặp lại đến khi heap còn 1 phần tử
  for i in (n-1).downto(0)
    swap(arr, 0, i);
    heapify(arr, i, 0);
  end
end

Heap sort là một thuật toán sắp xếp tại chỗ.
Độ phức tạp của heapify là O(logn), độ phức tạp của việc tạo và build heap là O(n). Vậy nên độ phức tạp của heap sort là O(nlogn) △

Tài liệu tham khảo
https://www.geeksforgeeks.org/binary-heap/