Bài toán Dining Philosophers trong java
Bài đăng này đã không được cập nhật trong 2 năm
1. Giới thiệu
Bài toán Dining Philosophers (Bữa tối của các triết gia) là một trong những vấn đề cổ điển được sử dụng để mô tả vấn đề đồng bộ hóa trong môi trường đa luồng và minh họa cách kỹ thuật để giải quyết chúng. Dijkstra lần đầu tiên đưa ra và trình bày vấn đề này liên quan đến các máy tính truy cập các thiết bị ngoại vi ổ băng từ.
Công thức hiện tại được đưa ra bởi Tony Hoare, người cũng được biết đến với việc phát minh ra thuật toán sắp xếp quicksort. Trong bài viết này chúng ta sẽ cùng phân tích vấn đề nổi tiếng này và viết mã theo một giải pháp phổ biến.
2. Bài toán
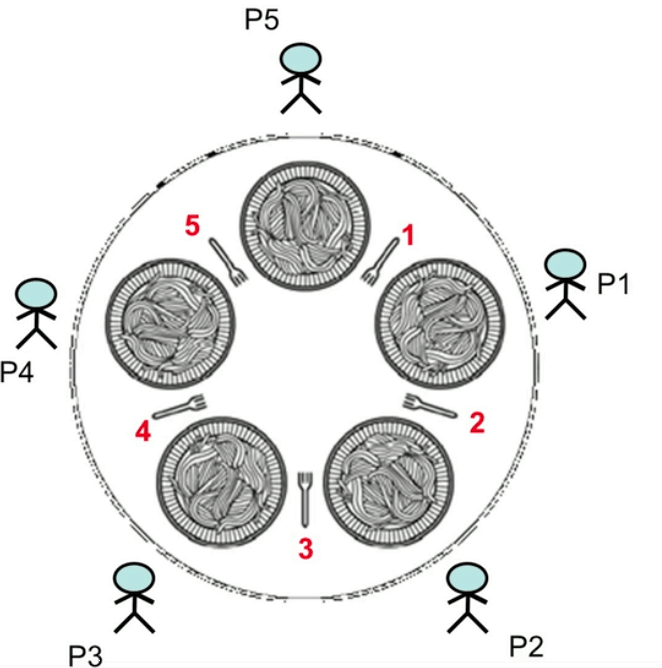
Sơ đồ trên đại diện cho vấn đề. Có năm triết gia im lặng (P1 – P5) ngồi quanh chiếc bàn tròn, dành cả đời để ăn và suy nghĩ.
Có năm chiếc nĩa để họ chia sẻ (1 – 5) và để có thể ăn, một triết gia cần phải cầm nĩa trên cả hai tay. Sau khi ăn xong, anh ta đặt cả hai thứ xuống và sau đó chúng có thể được chọn bởi một triết gia khác, người lặp lại chu kỳ tương tự.
Mục tiêu là đưa ra một sơ đồ/quy trình giúp các nhà triết học đạt được mục tiêu ăn uống và suy nghĩ mà không bị chết đói.
3. Giải pháp
Một giải pháp ban đầu sẽ là làm cho mỗi triết gia tuân theo giao thức sau:
while(true) {
// Initially, thinking about life, universe, and everything
think();
// Take a break from thinking, hungry now
pick_up_left_fork();
pick_up_right_fork();
eat();
put_down_right_fork();
put_down_left_fork();
// Not hungry anymore. Back to thinking!
}
Như đoạn mã ở trên mô tả, ban đầu mỗi triết gia đều suy nghĩ. Sau một khoảng thời gian nhất định, nhà triết học cảm thấy đói và muốn ăn.
Tại thời điểm này, anh ta với lấy chiếc nĩa ở hai bên và khi đã lấy được cả hai chiếc, anh ta sẽ tiếp tục ăn . Sau khi ăn xong, nhà triết học sẽ đặt nĩa xuống, để chúng có sẵn cho người bên cạnh của mình.
4. Implementation
Chúng ta lập mô hình từng triết gia của mình dưới dạng các lớp triển khai giao diện Runnable để chúng ta có thể chạy chúng dưới dạng các luồng riêng biệt. Mỗi Philosopher có quyền truy cập vào hai cái nĩa ở bên trái và bên phải của mình:
public class Philosopher implements Runnable {
// The forks on either side of this Philosopher
private Object leftFork;
private Object rightFork;
public Philosopher(Object leftFork, Object rightFork) {
this.leftFork = leftFork;
this.rightFork = rightFork;
}
@Override
public void run() {
// Yet to populate this method
}
}
Chúng ta cũng có một function hướng dẫn một Triết gia thực hiện một hành động – ăn, suy nghĩ hoặc lấy nĩa để chuẩn bị ăn:
public class Philosopher implements Runnable {
// Member variables, standard constructor
private void doAction(String action) throws InterruptedException {
System.out.println(
Thread.currentThread().getName() + " " + action);
Thread.sleep(((int) (Math.random() * 100)));
}
// Rest of the methods written earlier
}
Như được hiển thị trong đoạn mã trên, mỗi hành động được mô phỏng bằng cách tạm dừng luồng đang gọi trong một khoảng thời gian ngẫu nhiên, do đó lệnh thực thi không được thực thi chỉ theo thời gian.
Bây giờ, hãy triển khai logic cốt lõi của Philosopher .
Để mô phỏng việc lấy một cái nĩa, chúng ta cần khóa nó để không có hai luồng Philosopher nào lấy được nó cùng một lúc.
Để đạt được điều này, chúng tôi sử dụng từ khóa synchronized để có được internal monitor của đối tượng nĩa và ngăn các luồng khác thực hiện tương tự. Bây giờ chúng ta tiến hành triển khai phương thức run() trong lớp Philosopher :
public class Philosopher implements Runnable {
// Member variables, methods defined earlier
@Override
public void run() {
try {
while (true) {
// thinking
doAction(System.nanoTime() + ": Thinking");
synchronized (leftFork) {
doAction(
System.nanoTime()
+ ": Picked up left fork");
synchronized (rightFork) {
// eating
doAction(
System.nanoTime()
+ ": Picked up right fork - eating");
doAction(
System.nanoTime()
+ ": Put down right fork");
}
// Back to thinking
doAction(
System.nanoTime()
+ ": Put down left fork. Back to thinking");
}
}
} catch (InterruptedException e) {
Thread.currentThread().interrupt();
return;
}
}
}
Kế hoạch này thực hiện chính xác kế hoạch đã mô tả trước đó: một Triết gia suy nghĩ một lúc rồi quyết định ăn.
Sau đó, anh ta lấy nĩa ở bên trái và bên phải của mình và bắt đầu ăn. Khi làm xong, anh ta đặt nĩa xuống. Chúng ta cũng thêm dấu thời gian cho từng hành động, điều này sẽ giúp chúng ta hiểu thứ tự diễn ra các sự kiện.
Để bắt đầu toàn bộ quá trình, chúng tôi viết một ứng dụng khách tạo 5 Triết gia làm chủ đề và bắt đầu tất cả chúng:
public class DiningPhilosophers {
public static void main(String[] args) throws Exception {
Philosopher[] philosophers = new Philosopher[5];
Object[] forks = new Object[philosophers.length];
for (int i = 0; i < forks.length; i++) {
forks[i] = new Object();
}
for (int i = 0; i < philosophers.length; i++) {
Object leftFork = forks[i];
Object rightFork = forks[(i + 1) % forks.length];
philosophers[i] = new Philosopher(leftFork, rightFork);
Thread t
= new Thread(philosophers[i], "Philosopher " + (i + 1));
t.start();
}
}
}
Chúng tôi mô hình hóa từng nhánh như các đối tượng Java chung và tạo ra nhiều nhánh như số triết gia. Chúng tôi chuyển cho mỗi Triết gia các nhánh trái và phải của anh ấy mà anh ấy cố gắng khóa bằng từ khóa synchronized .
Chạy mã này dẫn đến kết quả đầu ra tương tự như sau. Đầu ra của bạn rất có thể sẽ khác với kết quả được đưa ra dưới đây, chủ yếu là do phương thức sleep() được gọi trong một khoảng thời gian khác:
Philosopher 1 8038014601251: Thinking
Philosopher 2 8038014828862: Thinking
Philosopher 3 8038015066722: Thinking
Philosopher 4 8038015284511: Thinking
Philosopher 5 8038015468564: Thinking
Philosopher 1 8038016857288: Picked up left fork
Philosopher 1 8038022332758: Picked up right fork - eating
Philosopher 3 8038028886069: Picked up left fork
Philosopher 4 8038063952219: Picked up left fork
Philosopher 1 8038067505168: Put down right fork
Philosopher 2 8038089505264: Picked up left fork
Philosopher 1 8038089505264: Put down left fork. Back to thinking
Philosopher 5 8038111040317: Picked up left fork
Tất cả các Philosopher ban đầu bắt đầu suy nghĩ, và chúng ta thấy rằng Philosopher 1 tiếp tục nhặt nĩa trái và phải, sau đó ăn và đặt cả hai xuống, sau đó Philosopher 5 nhặt nó lên.
5. Vấn đề với giải pháp: DeadLock
Mặc dù có vẻ như giải pháp trên là chính xác, nhưng vẫn có vấn đề deadlock phát sinh.
Deadlock là tình huống trong đó tiến trình của một hệ thống bị tạm dừng vì mỗi quy trình đang chờ để lấy tài nguyên do một số quy trình khác nắm giữ.
Chúng ta có thể xác nhận điều tương tự bằng cách chạy mã trên một vài lần và kiểm tra xem mã có bị treo không. Đây là một đầu ra mẫu thể hiện vấn đề trên:
Philosopher 1 8487540546530: Thinking
Philosopher 2 8487542012975: Thinking
Philosopher 3 8487543057508: Thinking
Philosopher 4 8487543318428: Thinking
Philosopher 5 8487544590144: Thinking
Philosopher 3 8487589069046: Picked up left fork
Philosopher 1 8487596641267: Picked up left fork
Philosopher 5 8487597646086: Picked up left fork
Philosopher 4 8487617680958: Picked up left fork
Philosopher 2 8487631148853: Picked up left fork
Trong tình huống này, mỗi Philosopher đều có được chiếc nĩa bên trái của mình, nhưng không thể có được chiếc nĩa bên phải của mình vì người bên cạnh của anh ta đã có được nó. Tình trạng này thường được gọi là vòng chờ đợi và là một trong những điều kiện dẫn đến deadlock và ngăn cản tiến trình của hệ thống.
6. Giải quyết deadlock
Như chúng ta đã thấy ở trên, lý do chính dẫn đến bế tắc là điều kiện chờ vòng tròn trong đó mỗi quy trình chờ một tài nguyên đang được nắm giữ bởi một số quy trình khác. Do đó, để tránh tình trạng bế tắc, chúng ta cần đảm bảo rằng điều kiện chờ vòng tròn bị phá vỡ. Có một số cách để đạt được điều này, cách đơn giản nhất là như sau:
Tất cả các Triết gia đều với tới chiếc nĩa bên trái của họ trước, ngoại trừ người đầu tiên với tới nĩa bên phải của mình.
Chúng ta triển khai điều này trong mã hiện tại của mình bằng cách thực hiện một thay đổi tương đối nhỏ trong mã:
public class DiningPhilosophers {
public static void main(String[] args) throws Exception {
final Philosopher[] philosophers = new Philosopher[5];
Object[] forks = new Object[philosophers.length];
for (int i = 0; i < forks.length; i++) {
forks[i] = new Object();
}
for (int i = 0; i < philosophers.length; i++) {
Object leftFork = forks[i];
Object rightFork = forks[(i + 1) % forks.length];
if (i == philosophers.length - 1) {
// The last philosopher picks up the right fork first
philosophers[i] = new Philosopher(rightFork, leftFork);
} else {
philosophers[i] = new Philosopher(leftFork, rightFork);
}
Thread t
= new Thread(philosophers[i], "Philosopher " + (i + 1));
t.start();
}
}
}
Sự thay đổi xuất hiện ở các dòng 17-19 của đoạn mã trên, nơi chúng ta đưa ra điều kiện khiến nhà triết học cuối cùng chạm tới nĩa bên phải của mình trước, thay vì bên trái. Điều này phá vỡ điều kiện chờ vòng tròn và chúng ta có thể ngăn chặn bế tắc.
Đầu ra sau đây cho thấy một trong những trường hợp mà tất cả các Triết gia đều có cơ hội suy nghĩ và ăn uống mà không gây ra bế tắc:
Philosopher 1 88519839556188: Thinking
Philosopher 2 88519840186495: Thinking
Philosopher 3 88519840647695: Thinking
Philosopher 4 88519840870182: Thinking
Philosopher 5 88519840956443: Thinking
Philosopher 3 88519864404195: Picked up left fork
Philosopher 5 88519871990082: Picked up left fork
Philosopher 4 88519874059504: Picked up left fork
Philosopher 5 88519876989405: Picked up right fork - eating
Philosopher 2 88519935045524: Picked up left fork
Philosopher 5 88519951109805: Put down right fork
Philosopher 4 88519997119634: Picked up right fork - eating
Philosopher 5 88519997113229: Put down left fork. Back to thinking
Philosopher 5 88520011135846: Thinking
Philosopher 1 88520011129013: Picked up left fork
Philosopher 4 88520028194269: Put down right fork
Philosopher 4 88520057160194: Put down left fork. Back to thinking
Philosopher 3 88520067162257: Picked up right fork - eating
Philosopher 4 88520067158414: Thinking
Philosopher 3 88520160247801: Put down right fork
Philosopher 4 88520249049308: Picked up left fork
Philosopher 3 88520249119769: Put down left fork. Back to thinking
Có thể xác minh bằng cách chạy mã nhiều lần để hệ thống thoát khỏi tình trạng bế tắc đã xảy ra trước đó.
7. Kết luận
Trong bài viết này, chúng ta đã khám phá vấn đề bữa tối của các triết gia nổi tiếng và các khái niệm về sự chờ đợi và bế tắc vòng tròn . Chúng ta đã mã hóa một giải pháp đơn giản gây ra bế tắc và thực hiện một thay đổi đơn giản để phá vỡ vòng chờ đợi và tránh bế tắc. Đây chỉ là một sự khởi đầu và các giải pháp phức tạp hơn vẫn tồn tại.
All rights reserved