10.5K 782 122

Đã đăng vào thg 6 8, 2022 6:15 SA 5 phút đọc

21.4K

Bài 7: Mảng hai chiều

I. Mảng hai chiều trong C++

1. Khai báo và truy xuất

Ngoài kiểu dữ liệu mảng một chiều, C++ hỗ trợ kiểu dữ liệu mảng từ hai chiều tới nhiều chiều. Mảng hai chiều là ví dụ rất trực quan và dễ tưởng tượng, ta có thể xem nó như một bảng hình chữ nhật gồm có $M$ hàng và $N$ cột. Cú pháp khai báo rất đơn giản:

{Kiểu_phần_tử} {Tên_mảng}[{Số_hàng}][{Số_cột}];

Khi đó, tổng số phần tử của mảng sẽ là {Số_hàng} $\times$ {Số_cột}. Chẳng hạn, khai báo một mảng hai chiều gồm $10$ hàng và $12$ cột chứa toàn số nguyên, ta viết như sau:

int a[10][12];

Các hàng và cột của mảng hai chiều đều sẽ được đánh số từ $0$ . Cách truy cập phần tử tương tự như ở mảng một chiều, chỉ cần dùng toán tử [] ở từng chiều để đưa ra một phần tử nào đó. Ví dụ, muốn truy cập phần tử ở hàng $3,$ cột $4,$ ta chỉ cần viết:

a[3][4];

Để tiện cho việc đánh số và biểu diễn trên hình, thường người ta sẽ quy ước đánh số các hàng từ trên xuống dưới và các cột từ trái qua phải:

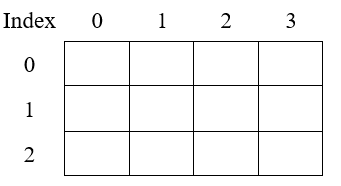
Tuy nhiên, có một lưu ý nho nhỏ, đó là khi khai báo mảng hai chiều các bạn không nên khai báo bằng biến cục bộ. Lí do là vì, khi khai báo biến cục bộ thì bộ nhớ cấp phát cho biến sẽ lưu trong stack của máy tính, và đối với một số trình biên dịch có thể gây ra lỗi không đáng có!

2. Khởi tạo mảng hai chiều

Giống như mảng một chiều, mảng hai chiều cũng có thể khởi tạo trước giá trị. Cú pháp như sau:

{Kiểu_phần_tử} {Tên_mảng}[{Số_hàng}][{Số_cột}] = 
{
    {{Danh_sách_phần_tử_của_hàng_0}};    
    {{Danh_sách_phần_tử_của_hàng_1}};
    ...
    {{Danh_sách_phần_tử_của_hàng_cuối}};
};

Ví dụ: Khởi tạo mảng hai chiều kích thước $3 \times 4$ gồm $12$ số nguyên:

int a[3][4] = 
{
    {1, 2, 3, 4};
    {5, 6, 7, 8};
    {9, 10, 11, 12};
};

Ngoài cách khởi tạo mảng với số phần tử cố định, trên mảng hai chiều cũng có thể khởi tạo với các cách không khai báo số lượng hàng, cột hoặc không khởi tạo hết các phần tử giống như mảng một chiều. Bạn đọc có thể tự mình cài đặt các cách khởi tạo khác nhau để kiểm chứng. Trong C++ không chỉ có mảng hai chiều, mà còn có mảng nhiều chiều, nhưng sẽ khá khó tưởng tượng và cũng không thường xuyên sử dụng, vì vậy chúng ta không cần đề cập đến ở đây.

3. Nhập xuất dữ liệu trên mảng hai chiều

Ví dụ dưới đây sẽ minh hoạt một chương trình yêu cầu nhập vào một mảng hai chiều kích thước $M\times N$ và in ra toàn bộ mảng đó theo thứ tự hàng cột. Bạn đọc có thể áp dụng đúng phương pháp này cho việc nhập và truy xuất dữ liệu trên các mảng $3$ chiều, $4$ chiều,...:

#include <iostream>

using namespace std;	
	
int main()
{
    int M, N;	
    cin >> M >> N;
        
    for (int i = 0; i < M; ++i)
        for (int j = 0; j < N; ++j)
            cin >> a[i][j];

    cout << "Mảng đã nhập vào là: " << endl;
    for (int i = 0; i < M; ++i)
    {
        for (int j = 0; j < N; ++j)
            cout << a[i][j] << ' ';

        cout << endl;
    }

    return 0;
}

Giả sử nhập vào mảng kích thước $3 \times 4$ với các giá trị từ $1$ tới $12,$ chạy chương trình sẽ thu được kết quả sau:

Mảng đã nhập vào là:
1 2 3 4
5 6 7 8
9 10 11 12

II. Một vài bài toán với mảng hai chiều

1. Tìm giá trị lớn nhất trong mảng hai chiều

Đề bài

Cho mảng hai chiều $A$ gồm $m$ hàng $n$ cột, các hàng được đánh số từ $1$ tới $m$ từ trên xuống dưới, các cột được đánh số từ $1$ tới $n$ từ trái qua phải. Ô nằm trên giao của hàng $i,$ cột $j$ gọi là ô $(i, j)$ và có chứa số nguyên $a_{i, j}$ .

Yêu cầu: Hãy xác định giá trị lớn nhất trong mảng $A?$

Input:

Dòng đầu tiên chứa hai số nguyên dương $m, n$ - kích thước mảng hai chiều.
Trên $m$ dòng tiếp theo, mỗi dòng chứa $n$ số nguyên $a_{i, j}$ thể hiện hàng thứ $i$ của mảng.

Ràng buộc:

$1 \le m, n \le 1000$ .
$1 \le a_{i, j} \le 10^9; \forall i, j: 1 \le i \le m, 1 \le j \le n$ .

Output:

In ra giá trị lớn nhất trong mảng $A$ .

Sample Input:

4 5
1 2 3 4 5
-1 -2 0 3 5
10 4 -5 -10 6
4 4 4 4 4

Sample Output:

Ý tưởng

Sử dụng kĩ thuật đặt cờ, gán một biến $res = a_{1, 1}$ để coi như phần tử lớn nhất trong mảng là $a_{1, 1}$ . Sau đó duyệt qua tất cả các giá trị trong bảng, nếu phần tử nào lớn hơn $res$ thì cập nhật lại $res$ bằng phần tử đó.

Kết quả cuối cùng chính là $res$ .

Cài đặt

#include <bits/stdc++.h>

using namespace std;

int a[1001][1001];

main()
{
    int m, n;
    cin >> m >> n;
	
    for (int i = 1; i <= m; ++i)
        for (int j = 1; j <= n; ++j)
            cin >> a[i][j];

    int res = a[1][1];
    for (int i = 1; i <= m; ++i)
        for (int j = 1; j <= n; ++j)
            if (a[i][j] > res)
                res = a[i][j];

    cout << res;

    return 0;
}

2. Tính tổng các phần tử trong mảng

Đề bài

Yêu cầu: Hãy tính tổng các phần tử trong mảng?

Input:

Dòng đầu tiên chứa hai số nguyên dương $m, n$ - kích thước mảng hai chiều.
Trên $m$ dòng tiếp theo, mỗi dòng chứa $n$ số nguyên $a_{i, j}$ thể hiện hàng thứ $i$ của mảng.,

Ràng buộc:

$1 \le m, n \le 1000$ .
$1 \le a_{i, j} \le 10^9; \forall i, j: 1 \le i \le m, 1 \le j \le n$ .

Output:

Số nguyên duy nhất là tổng các phần tử trong mảng.

Sample Input:

Sample Output:

Ý tưởng

Giống như mảng một chiều, chúng ta chỉ cần sử dụng một biến $sum$ để lưu tổng các phần tử trong mảng, rồi duyệt qua toàn bộ các phần tử và tính tổng của chúng.

Cài đặt

#include <bits/stdc++.h>

using namespace std;

int a[1001][1001];

main()
{
    int m, n;
    cin >> m >> n;
	
    int sum = 0;
    for (int i = 1; i <= m; ++i)
        for (int j = 1; j <= n; ++j)
        {
            cin >> a[i][j];
            sum += a[i][j];
        }

    cout << sum;

    return 0;
}

3. Tổng đường chéo

Đề bài

Cho mảng hai chiều dạng vuông $A$ gồm $m$ hàng $m$ cột, các hàng được đánh số từ $1$ tới $m$ từ trên xuống dưới, các cột được đánh số từ $1$ tới $n$ từ trái qua phải. Ô nằm trên giao của hàng $i,$ cột $j$ gọi là ô $(i, j)$ và có chứa số nguyên $a_{i, j}$ .

Đường chéo chính của ma trận là đường chéo nối ô $(1, 1)$ với ô $(m, m)$ . Đường chéo phụ của ma trận là đường chéo nối ô $(1, m)$ với ô $(m, 1)$ .

Yêu cầu: Hãy tính tổng các số trên đường chéo chính và đường chéo phụ của ma trận vuông?

Input:

Dòng đầu tiên chứa hai số nguyên dương $m, n$ - kích thước mảng hai chiều.
Trên $m$ dòng tiếp theo, mỗi dòng chứa $n$ số nguyên $a_{i, j}$ thể hiện hàng thứ $i$ của mảng.,

Ràng buộc:

$1 \le m, n \le 1000$ .
$1 \le a_{i, j} \le 10^9; \forall i, j: 1 \le i \le m, 1 \le j \le n$ .

Output:

Hai số nguyên lần lượt là tổng đường chéo chính và tổng đường chéo phụ của ma trận.

Sample Input:

Sample Output:

6 4

Ý tưởng

Một ô $(i, j)$ sẽ thuộc đường chéo chính của ma trận nếu như $i = j$ . Còn nếu như $i = m - i + 1,$ thì ô đó sẽ thuộc đường chéo phụ của ma trận.

Ta duyệt qua các phần tử của ma trận và kết hợp câu lệnh if để tính tổng hai đường chéo.

Cài đặt

#include <bits/stdc++.h>

using namespace std;

int a[1001][1001];

int main()
{
    int m;
    cin >> m;

    for (int i = 1; i <= m; ++i)
        for (int j = 1; j <= m; ++j)
            cin >> a[i][j];

    long long main_diagonal = 0, secondary_diagonal = 0;
    for (int i = 1; i <= N; ++i)
        for (int j = 1; j <= N; ++j)
        {
            if (i == j)
                main_diagonal += a[i][j];
            if (j == m - i + 1)
                secondary_diagonal += a[i][j];
        }

    cout << main_diagonal << ' ' << secondary_diagonal;

    return 0;
}

III. Tài liệu tham khảo

I. Mảng hai chiều trong C++

1. Khai báo và truy xuất

2. Khởi tạo mảng hai chiều

3. Nhập xuất dữ liệu trên mảng hai chiều

II. Một vài bài toán với mảng hai chiều

1. Tìm giá trị lớn nhất trong mảng hai chiều

Đề bài

Ý tưởng

Cài đặt

2. Tính tổng các phần tử trong mảng

Đề bài

Ý tưởng

Cài đặt

3. Tổng đường chéo

Đề bài

Ý tưởng

Cài đặt

III. Tài liệu tham khảo

Mục lục