Applicative Functor

Bài đăng này đã không được cập nhật trong 9 năm

Trong Scala chúng ta sẽ bắt gặp nhiều đến khái niệm Applicative Functor, thực ra khái niệm này có từ ngôn ngữ Haskell. Về bản chất Applicative Funtor là những functor được bổ sung thêm một vài thuộc tính. Trong bài này chúng ta sẽ bóc tách và tìm hiểu về functor, các thuộc tính applicative.

Chú Ý: Bạn cần có kiến thức cơ bản về syntax của scala để có thể hiểu được những đoạn code ví dụ trong bài này

Functor

Định nghĩa functor:

trait GenericFunctor[->>[_, _], ->>>[_, _], F[_]] {

  def fmap[A, B](f: A ->> B): F[A] ->>> F[B]
}

trait Functor[F[_]] extends GenericFunctor[Function, Function, F] {

  final def fmap[A, B](as: F[A])(f: A => B): F[B] =
    fmap(f)(as)
}

Để đơn giản hóa, chúng ta sẽ sử dụng định nghĩa cụ thể hơn về functor, như functor là một endofunctor, vì source và target của nó là một. Có thể bạn sẽ nhớ ra rằng một functor như thế có thể được coi như là một provider của một computational context: một function f:A => B cho một fmap được đưa vào context của functor đó, có nghĩa rằng nó được thực thi dưới sự kiểm soát của functor đó (có thể một lần, nhiều lần, hoặc chẳng có lần nào cả).

fmap

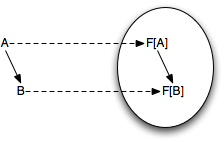
Chúng ta có một ví dụ về OptionFunctor, nếu fmap được truyền giá trị Some thì function truyền vào sẽ được gọi, và ngược với giá trị none.

scala> fmap(Option(1)) { x => println("I was invoked!"); x + 1 }
I was invoked!
res0: Option[Int] = Some(2)

scala> fmap(None: Option[Int]) { x => println("I was invoked!"); x + 1 }
res1: Option[Int] = None

Sử dụng functor chúng ta có thể chuyển các function từ arity-1 thành các computational context.

Applicatives

Nhưng sẽ thế nào nếu chúng ta có một function với arity cao hơn? chúng ta vẫn sẽ sử dụng một functor để đưa nó thành một function arity-2.

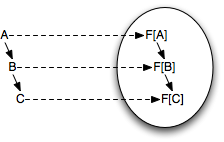
arity-2

Hãy xem chuyện gì sẽ xảy ra nếu chúng ta gọi fmap từng phần để áp dụng một function arity-2 cho đối số đầu tiên trong computational context của một Option:

scala> val f = (x: Int) => (y: Int) => x + y + 10
f: (Int) => (Int) => Int = <function1>

scala> fmap(Option(1))(f)
res0: Option[(Int) => Int] = Some()

Cái mà chúng ta nhận được là một Option[Int => Int], là những gì "còn lại", của function mà nó được áp dụng một phần, được gói vào một Option. Tới đây thì chúng ta gặp vấn đề là không thể đưa function này vào một lời gọi khác của fmap.

scala> fmap(Option(2))(fmap(Option(1))(f))
:13: error: type mismatch;
 found   : Option[(Int) => Int]
 required: (Int) => ?
       fmap(Option(2))(fmap(Option(1))(f))

Nguyên nhân là do fmap chỉ nhận một pure function, không phải lifted funtion. Và đó chính là lúc chúng ta phải áp dụng applicatives. Ý tưởng rất đơn giản và nó diễn ra theo hướng suy nghĩ từ những gì chúng ta vừa thấy: thay vì fmap chỉ nhận một pure function, một Applicative định nghĩa function apply, nhận một lifted function. Và nó định nghĩa method pure để lift pure functions. Cách này hoàn toàn có thể áp dụng một cách từng phần vào một arity-n function cho tất cả các đối số trong một computational context. Trước khi chúng ta sửa code theo hướng mới, hãy tạo ra abstraction mới:

trait Applicative[F[_]] extends Functor[F] {

  def pure[A](a: A): F[A]

  def apply[A, B](f: F[A => B]): F[A] => F[B]

  final def apply[A, B](fa: F[A])(f: F[A => B]): F[B] =
    apply(f)(fa)

  override def fmap[A, B](f: A => B): F[A] => F[B] =
    apply(pure(f))
}

Như bạn có thể thấy, có một mối liên kết rất rõ ràng giữa các functors và applicatives: mỗi applicative là một functor và với mỗi law cho applicatives thì điều sau đây phải đúng: fmap = apply o pure. Điều này là khá hiển nhiên vì nó đảm bảo là chúng ta có thể sử dụng một applicative như là một functor, ví dụ với một pure arity-1 function và nó sẽ hoạt động đúng như ta mong đợi.

Để làm việc với các applicatives chúng ta cần một vài bản mẫu, đối với ví dụ Option chúng ta cần một Applicative như sau:

object Applicative {

  def pure[A, F[_]](a: A)(implicit applicative: Applicative[F]): F[A] =
    applicative pure a

  def apply[A, B, F[_]](fa: F[A])(f: F[A => B])(implicit applicative: Applicative[F]): F[B] =
    applicative.apply(fa)(f)

  implicit object OptionApplicative extends Applicative[Option] {

    override def pure[A](a: A): Option[A] =
      Option(a)

    override def apply[A, B](f: Option[A => B]): Option[A] => Option[B] =
      o => for { a <- o; p <- f } yield p(a)
    }
}

bây giờ hãy cùng nhìn ví dụ của chúng ta về arity-2 function. Sử dụng một functor mà chúng ta đã bế tắc ở phần trước, nhưng bằng việc sử dụng một applicative chúng ta có thể làm nó hoạt động thông qua 2 đối số:

scala> apply(Option(1))(apply(Option(2))(pure(f)))
res0: Option[Int] = Some(13)

Đoạn code này trông có vẻ lởm và thừa thãi. Đối số thứ nhất, ok. Đối số thứ hai, chúng ta hiển nhiên ko cần một applicative cho Option vì đã có flatMap. Nhưng với cách tiếp cận này chúng ta có thể giải quyết được bất kỳ class nào, ví dụ Either của thư viện chuẩn Scala hay các classes từ chính dự án của bạn.

Kết Luận

Những nguyên tắc cơ bản của applicatives là chúng ta có thể áp dụng các functions của các arity-n cho các đối số trong một computational context. Functors bản thân nó đã thỏa mãn cho arity-1, applicatives chính là những functors được khái quát hóa.

Nhờ sự linh hoạt của Scala, chúng ta có thể làm được nhiều hơn nữa. Nhưng thay vì tự xây dựng các pattern này, cộng đồng scalaz đã làm điều đó một cách rất tốt, dưới đây là 2 cách thay thế cho ví dụ trên sử dụng thư viện này:

scala> Option(1) <*> (Option(2) <*> Option(f))
res0: Option[Int] = Some(13)

scala> (Option(1) <**> Option(2)) { _ + _ + 10 }
res1: Option[Int] = Some(13)

Vi dụ thứ hai thực sự trông rất rõ ràng và dễ hiểu. Và chúng ta có thể sử dụng nó cho những types không có các methods hữu dụng như flatMap. Dưới đây là một ví dụ khác sử dụng Either:

scala> (1.right[String] <**> 2.right[String]) { _ + _ + 10 }
res0: Either[String,Int] = Right(13)

scala> (1.right[String] <**> "Error".left[Int]) { _ + _ + 10 }
res1: Either[String,Int] = Left(Error)

Tham khảo

Scala

Functor

Applicatives

Kết Luận

Tham khảo

Mục lục