Algorithms for Transformer

1. Token embedding

Token embedding là quá trình biểu diễn 1 token ( từ hoặc kí tự..) trong 1 đầu vào dưới dạng vector số.

Input : token ID

Output : vector đại diện của token

Qúa trình hoạt động :

B1 : Đầu vào sẽ là 1 chuỗi các từ hoặc kí tự được xử lý dưới dạng token ID

B2 : Sử dụng mã số ID của từ này để lấy vector tương ứng trong ma trận embedding

( Mình sẽ giải thích rõ B2 này như sau, chúng ta sẽ sử dụng token ID đã nêu ở trên để truy xuất vào ma trận embedding . Ma trận embedding chứa các vector được huấn luyện trước đó và được biểu diễn bởi các hàng, mỗi hàng tương ứng với 1 token, do vậy chúng ta có thể truy xuất đến vector của 1 từ bằng cách sử dụng ID của từ đó. Ví dụ, trong từ điển của chúng ta, nếu từ dog có ID là 102, chúng ta sẽ truy xuất vector embedding tương ứng bằng cách lấy hàng thứ 102 của ma trận embedding)

B3 : Vector này sẽ được sử dụng làm vector đại diện của từ này trong model

Mình sẽ đưa ra 1 ví dụ cụ thể như sau : “Tôi có một con chó”

Ta sẽ có 1 từ điển gồm các từ sau :

{
  "tôi": 0,
  "có": 1,
  "một": 2,
  "con": 3,
  "chó": 4
}

Và 1 ma trận embedding (ma trận này đã được huấn luyện trên 1 tập dữ liệu lớn )

[
 [0.1, 0.2, 0.3, 0.4],
 [0.2, 0.3, 0.4, 0.5],
 [0.3, 0.4, 0.5, 0.6],
 [0.4, 0.5, 0.6, 0.7],
 [0.5, 0.6, 0.7, 0.8],
 [0.0, 0.0, 0.0, 0.0]  # token đặc biệt để đại diện các từ chưa có trong từ điển
]

Từ đó, ta sẽ thu được các vector embedding(vector đại diện) tương ứng như sau :

[ [0.1, 0.2, 0.3, 0.4],  # vector embedding của "tôi"
 [0.2, 0.3, 0.4, 0.5],  # vector embedding của "có"
 [0.3, 0.4, 0.5, 0.6],  # vector embedding của "một"
 [0.4, 0.5, 0.6, 0.7],  # vector embedding của "con"
 [0.5, 0.6, 0.7, 0.8]   # vector embedding của "chó"
]

2. Positional embedding

Positional embedding sẽ học để biểu diễn vị trí của token trong 1 câu dưới dạng 1 vector.

Mục đích của positional embedding là cho phép Transformer model hiểu về thứ tự từ.

Input : vị trí của token trong câu

Output: vector đại diện cho vị trí đó trong không gian

Để tìm ra vector positional embedding ta cần tìm vector Positional Encoding rồi sau đó cộng với vector embedding đã tìm được ở mục 1.

Đây là công thức tính vector PE :

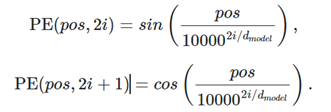
Trong đó :

• pos: vị trí của từ trong câu
• i: chỉ số của chiều trong vector embedding (từ 0 đến d-1)
• d: số chiều của vector embedding

Ví dụ tiếp với câu : Tôi có một con chó

• Ở mục 1 ta đã tính được vector embedding của nó như sau :

[
 [0.1, 0.2, 0.3, 0.4],  # vector embedding của "tôi"
 [0.2, 0.3, 0.4, 0.5],  # vector embedding của "có"
 [0.3, 0.4, 0.5, 0.6],  # vector embedding của "một"
 [0.4, 0.5, 0.6, 0.7],  # vector embedding của "con"
 [0.5, 0.6, 0.7, 0.8]   # vector embedding của "chó"
]

• B1 : Xét từ “tôi” có pos = 0 :

i=0 => P(0,0)=sin(0/10000^(0/4))=0
i=0 =>P(0,1)=cos(0/10000^(0/4)=1
i=1=>P(0,2)=0
i=1 =>P(0,3)=1

Từ đó suy ra vector PE = [0,1,0,1]

Trong mô hình Transformer, mỗi từ trong câu được biểu diễn bằng một vector có cùng số chiều, nếu chỉ sử dụng positional encoding 1 chiều thì các từ ở vị trí gần nhau sẽ có vector biểu diễn gần giống nhau, dẫn đến mô hình khó khăn trong việc học và phân loại các từ theo vị trí. Vì vậy, cần sử dụng positional encoding 2 chiều để đảm bảo rằng các từ ở các vị trí khác nhau sẽ có vector biểu diễn khác nhau và giúp mô hình học được sự phân bố của các từ trong câu.

Tính lần lượt với các trường hợp còn lại

• B2 : Cộng positional encoding vào vector embedding tương ứng :

[0.1, 0.2, 0.3, 0.4] + [0,1,0,1]=[0.1,1.2,0.3,1.4]

3. Attention

Thuật toán attention được sử dụng trong các mô hình Deep Learning để tập trung vào các phần quan trọng của đầu vào. Nó cho phép mô hình "tập trung" vào các phần của đầu vào mà có ý nghĩa cho đầu ra mà mô hình đang dự đoán.

Để tính attention, ta cần đi qua những bước sau đây, lấy ví dụ với 1 câu có 4 từ :

words = array([word_1, word_2, word_3, word_4])

• B1:

word_1 = array([1, 0, 0])
word_2 = array([0, 1, 0])
word_3 = array([1, 1, 0])
word_4 = array([0, 0, 1])

• B2 : Tạo ra ma trận trọng số

W_Q = [[0 1 1]
       [2 0 2]
       [2 1 0]]
                 
W_K =  [[0 1 2]
	    [0 2 1]
        [2 0 1]]
               
W_V = [[0 2 2] 
	   [0 0 0]
       [0 1 0]]

• B3: Tính query, key và value

Query_1 = word_1 x W_Q
Key_1 = word_1 x W_K
Value_1 = word_1 x W_V

Tương tự với các từ khác

Matrix của từ đầu tiên =  
         [[0 1 1]              #Q_1
          [0 1 2]              #K_1
          [0 2 2]]            #V_1

Tổng quan ta có :

Q = words x W_Q
K= words x W_K
V = words x W_V

• B4: Tính score

Score = (K^T) x Q            

(K^T là ma trận chuyển vị của K)

Suy ra : Score = [3,3,6,1]

• B5: Tính weight

weights = softmax(scores / K.shape[1] ** 0.5)

Trong phép tính trên, để tính ma trận trọng số attention, ta sử dụng hàm softmax trên mỗi hàng của ma trận điểm số, sau đó chia cho căn bậc hai của kích thước của ma trận key theo chiều thứ nhất . Theo cách sử dụng thông thường, trong các phép tính attention của Transformer, chiều đầu tiên của ma trận key thường tương ứng với số lượng các vector Key được sử dụng trong phép tính attention đó.

• B6 : Tính attention

Attention = weights x V

Kết quả là :

 [[0.98522025 1.74174051 0.75652026]
 [0.90965265 1.40965265 0.5       ]
 [0.99851226 1.75849334 0.75998108]
 [0.99560386 1.90407309 0.90846923]]

Mình sẽ giải thích kết quả này như sau, mỗi hàng sẽ tương ứng với attention của mỗi từ, trong đó lần lượt là xác suất của từ đang xét với các từ còn lại. Nếu xác suất càng lớn thì mức độ tương đồng của nó càng cao. Ví dụ như hàng đầu tiên chính là các xác suất cho sự tương đồng của từ đầu tiên so với các từ còn lại.

Như vậy, attention giúp mô hình tập trung vào những phần quan trọng của đầu vào bằng cách tính toán trọng số cho từng phần tử trong chuỗi đầu vào. Điều này giúp giảm thiểu sự ảnh hưởng của những phần không quan trọng, đồng thời cải thiện độ chính xác và hiệu suất của mô hình.