A* Search Algorithm
Bài đăng này đã không được cập nhật trong 4 năm
What is A* Search Algorithm?
A* (pronounced as "A star") is a computer algorithm that is widely used in pathfinding and graph traversal. The algorithm efficiently plots a walkable path between multiple nodes, or points, on the graph.
How it works?
Imagine a square grid which possesses many obstacles, scattered randomly. The initial and the final cell is provided. The aim is to reach the final cell in the shortest amount of time.

Explanation
A* works by making a lowest-cost path tree from the start node to the target node. What makes A* different and better for many searches is that for each node, A* uses a function f(n)f(n) that gives an estimate of the total cost of a path using that node. Therefore, A* is a heuristic function, which differs from an algorithm in that a heuristic is more of an estimate and is not necessarily provably correct.
A* expands paths that are already less expensive by using this function:
f(n)=g(n)+h(n)
- f(n) = total estimated cost of path through node nn
- g(n) = cost so far to reach node nn
- h(n) = estimated cost from nn to goal. This is the heuristic part of the cost function, so it is like a guess.
Pseudocode
function reconstruct_path(cameFrom, current)
total_path := {current}
while current in cameFrom.Keys:
current := cameFrom[current]
total_path.prepend(current)
return total_path
// A* finds a path from start to goal.
// h is the heuristic function. h(n) estimates the cost to reach goal from node n.
function A_Star(start, goal, h)
// The set of discovered nodes that may need to be (re-)expanded.
// Initially, only the start node is known.
// This is usually implemented as a min-heap or priority queue rather than a hash-set.
openSet := {start}
// For node n, cameFrom[n] is the node immediately preceding it on the cheapest path from start
// to n currently known.
cameFrom := an empty map
// For node n, gScore[n] is the cost of the cheapest path from start to n currently known.
gScore := map with default value of Infinity
gScore[start] := 0
// For node n, fScore[n] := gScore[n] + h(n). fScore[n] represents our current best guess as to
// how short a path from start to finish can be if it goes through n.
fScore := map with default value of Infinity
fScore[start] := h(start)
while openSet is not empty
// This operation can occur in O(1) time if openSet is a min-heap or a priority queue
current := the node in openSet having the lowest fScore[] value
if current = goal
return reconstruct_path(cameFrom, current)
openSet.Remove(current)
for each neighbor of current
// d(current,neighbor) is the weight of the edge from current to neighbor
// tentative_gScore is the distance from start to the neighbor through current
tentative_gScore := gScore[current] + d(current, neighbor)
if tentative_gScore < gScore[neighbor]
// This path to neighbor is better than any previous one. Record it!
cameFrom[neighbor] := current
gScore[neighbor] := tentative_gScore
fScore[neighbor] := gScore[neighbor] + h(neighbor)
if neighbor not in openSet
openSet.add(neighbor)
// Open set is empty but goal was never reached
return failure
Example
An example of an A* algorithm in action where nodes are cities connected with roads and h(x) is the straight-line distance to target point:
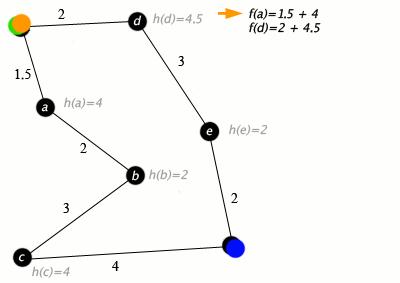
Key: green: start; blue: goal; orange: visited
Reference: https://en.wikipedia.org, https://brilliant.org/wiki, https://www.educative.io
All rights reserved